Тема урока : «Параллельный перенос»
Цели урока : дать понятие параллельного переноса, доказать, что параллельный перенос есть движение, учить выполнять параллельный перенос различных фигур.
Задачи : 1. Обучающая: Закрепить знания по осевой и центральной симметрии. Установить что такое параллельный перенос. Учиться выполнять параллельный перенос и применять его при решении задач.
2. Развивающая: Развивать логическое мышление, умение доказательно развивать свою мысль и умение делать выводы.
3. Воспитывающая: Формирование умения работать в коллективе. Воспитывать умение делать собственный выбор.
Тип урока: урок усвоения нового материала.
Вид урока: комбинированный урок с элементами беседы.
Метод обучения: частично-поисковый.
Ход Урока.
1. Организационный момент
2. Актуализация опорных знаний.
1. Что называется отображением плоскости на себя?
Если выполняются следующие условия: 1) каждой точке плоскости ставится в соответствие какая-то одна точка плоскости и 2) каждая точка плоскости оказывается поставленной в соответствие какой-то точке плоскости, то принято говорить, что дано отображение плоскости на себя.
1. Что такое движение? Назвать известные вам движения
Движение – это отображение плоскости на себя, сохраняющее расстояние, то есть расстояние между соответствующими точками сохраняется.
Примерами движения служат осевая и центральная симметрия.
При движении:
· отрезок отображается на равный ему отрезок
· треугольник отображается на равный ему треугольник
· угол отображается на равный ему угол
· луч отображается на луч
· прямая отображается на прямую
· любая фигура отображается на равную ей фигуру.
3. Что такое осевая симметрия?
· Преобразование, при котором каждая точка А фигуры преобразуется в симметричную ей относительно некоторой оси l точку А 1 , при этом отрезок АА 1  l и АК=КА 1 , называется осевой симметрией.
l и АК=КА 1 , называется осевой симметрией.
4. Рассказать о центральной симметрии.
· Преобразование, переводящее каждую точку А фигуры в точку А1, симметричную ей относительно центра О, называется преобразованием центральной симметрии или просто центральной симметрией. Точка О называется центром симметрии и является неподвижной.
5. Математический диктант.
1. Отметьте точки К и М. Постройте точку К 1, симметричную точке К относительно точки М.
2. Начертите прямую а и точку В вне ее. Постройте точку В 1, симметричную точке В относительно прямой а.
3. Закончите предложение: «Преобразование фигуры F в фигуру F1 называется движением, если оно ...».
4. Треугольники АВС и МКР симметричны относительно некоторой точки. Стороны ΔАВС равны 3 см, 4 см и 5 см. Найти периметр ΔМКР.
5. Два ромба симметричны друг другу относительно некоторой прямой. У первого ромба имеется прямой угол. Будет ли второй ромб квадратом?
6. В какую фигуру переходит при движении отрезок длиной в 3 см?
10. Проверка диктанта (друг у друга – оценка).
3. Изучение новой темы .
1. Какие прямые называются параллельными?
2.Свойство сторон параллелограмма. (В параллелограмме противоположные стороны равны).
3. Что такое вектор?
Параллельный перенос. Что знакомо в названии?
Видео урок
Как вы думаете, что нужно знать, чтобы выполнить параллельный перенос?
(Определение: Преобразование, при котором каждая точка фигуры перемещается в одном и том же направлении на одно и то же расстояние, называется параллельным переносом.
Чтобы задать преобразование параллельного переноса, достаточно задать вектор а ).
Докажем, что параллельный перенос – движение.
Для параллельного переноса имеют место следующие свойства:
1) отрезок переходит в равный ему отрезок;
2) угол переходит в равный ему угол;
3) окружность переходит в равную ей окружность;
4) любой многоугольник переходит в равный ему многоугольник;
5) параллельные прямые переходят в параллельные прямые;
6) перпендикулярные прямые переходят в перпендикулярные прямые.
4. Закрепление темы. Решаем №484, 486
5. Разноуровневая практическая работа

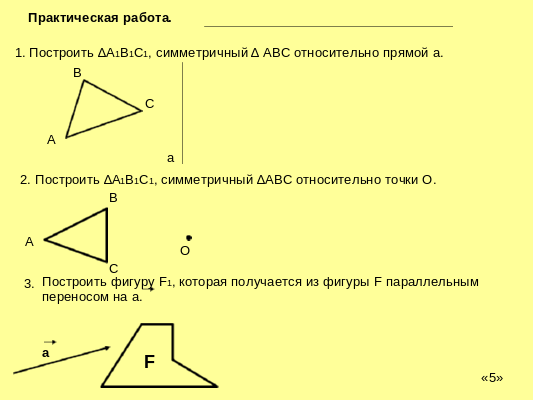
6. Итог урока.
Какое отображение плоскости называется параллельным переносом?
Приведите примеры из жизни, где вы встречались с параллельным переносом.
7. Задание на дом: п 57, №485, №488








