2. ЛХ линейных сау 3-х типов.
3. Годографы для анализа автоколебаний в нелинейных САУ 3-х типов.
4. Семейства ЛХ линеаризованных САУ.
5. Осциллограммы переходных процессов линейных САУ 3-х типов.
6. Результаты экспериментального анализа автоколебаний в нелинейных САУ 3-х типов.
7. Значения пороговых уровней шума, при которых выполняются условия статистической линеаризации нелинейных САУ 3-х типов.
8. Усредненные переходные процессы для 2-х значений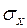 
.
9. Оценки фильтрующих свойств всех САУ.
8.4. Контрольные вопросы
1. Как влияют цепи коррекции на переходные процессы линейных САУ?
2. Как определяются амплитуда и частота автоколебаний в нелинейных САУ?
3. Влияет ли уровень шума на качество переходных процессов в линейных САУ?
4. Влияет ли уровень шума на качество переходных процессов в нелинейных САУ?
5. Объяснить эффект срыва автоколебаний в нелинейной САУ при действии шума.
6. Как изменяется коэффициент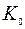 
при увеличении уровня шума и какие показатели качества линеаризованной САУ при этом меняются?
9. Исследование нелинейных элементов методом статистической линеаризации (лабораторная работа 8)
Цель работы – экспериментальная оценка статистических характеристик безынерционных нелинейных элементов, используемых в методе статистической линеаризации нелинейных САУ.
9.1. Описание лабораторной установки
Лабораторная установка включает в себя макет для исследования нелинейных элементов, внешний генератор широкополосных случайных процессов и осциллограф. Предусмотрена возможность исследования нелинейных элементов 3-х типов: идеальное реле, реле с зоной нечувствительности и реле с петлей гистерезиса. На вход каждого из этих элементов подается случайный процесс x(t) с нормальным законом распределения и регулируемыми параметрами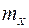 
(математическое ожидание) и 
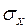(среднеквадратичное значение). Измерительная схема позволяет оценивать выходные параметры: 
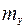и 
.
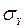В соответствии с методом статистической линеаризации нелинейный элемент заменяется эквивалентным ему (в смысле равенства математических ожиданий и дисперсий выходных процессов) линейным элементом, на выходе которого имеем
,
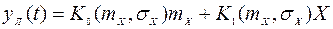где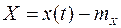 
- центрированная случайная компонента входного процесса x(t); 
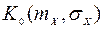и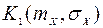 
- статистические коэффициенты усиления для математического ожидания 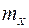и, соответственно, центрированной случайной компоненты X(t). Коэффициенты 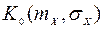и 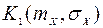можно экспериментально вычислить как крутизну зависимосте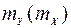й 
и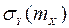 
в рабочей точке 
.
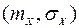Для определения динамических и точностных свойств нелинейных САУ наибольший интерес представляет коэффициент 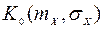, который связывает процесс 
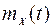с полезным воздействием. Как правило, наличие нелинейного элемента в САУ обусловлено нелинейностью статической характеристики дискриминатора. Если САУ обладает высокой точностью и хорошими сглаживающими свойствами, то ошибку системы ( 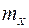) можно приближенно считать равной нулю. Тогда
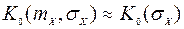при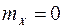 
и функцию передачи линеаризованной САУ в разомкнутом состоянии можно аппроксимировать выражением
,
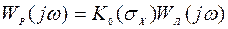где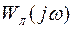 
- функция передачи линейной части САУ.
Замечание. В основу метода статистической линеаризации заложена аппроксимация функции плотности распределения вероятностей случайного процесса на выходе нелинейного элемента нормальным законом. Для обоснования такой аппроксимации необходимо наличие в функции передачи 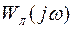инерционных звеньев.
Таким образом, уровень случайного процесса на выходе нелинейного элемента существенно влияет на коэффициент усиления разомкнутой САУ с соответствующими последствиями (например, изменяются качество переходных процессов и точность в установившемся режиме).
9.2. Задание по работе
1. Ознакомиться с лабораторным макетом и представленной на нем схемой измерений. Схему экспериментальных исследований и статические характеристики y(x) нелинейных элементов зарисовать.
2. Снять экспериментальные характеристик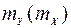и и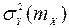 
при нескольких значениях уровня шума 
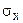(уровень шума отсчитывается в условных значениях по шкале потенциометра).
3. Для каждого нелинейного элемента построить 2 семейства графиков: 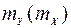и 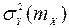при выбранных значениях уровня шума .
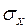4. С физических позиций дать объяснение полученным результатам. Для этого следует рассмотреть прохождение через нелинейный элемент нормального случайного процесса с заданными параметрам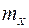и и 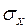и оперировать плотностью распределения вероятностей W(y).
5. Используя полученные в результате эксперимента зависимости 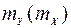, определить 
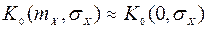и построить зависимости 
.
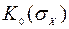9.3. Контрольные вопросы
1. Каким образом параметры 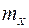и 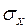влияют на вид функции W(y)?
2. Дать физическую трактовку зависимосте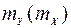й и .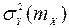
3. Как влияет уровень шума на входе нелинейного элемента на показатели качества нелинейной САУ?