4. Привести расчетные соотношения и результаты вычислений значения KОПТ двумя способами.
5. Сопоставить результаты эксперимента с теоретическими сведениями. Подтвердить наличие корреляции процессов g(t) и v(t).
6. Построить семейство ЛХ и АЧХ САУ для нескольких значений параметра K (в том числе – для расчетного значения KОПТ).
7.3. Содержание отчета
1. Структурная схема исследуемой САУ.
2. Основные расчетные соотношения.
3. Экспериментальные зависимости по пп.1-4 задания.
4. Семейства ЛХ и АЧХ.
5. Выводы по результатам экспериментальных исследований.
7.4. Контрольные вопросы
1. С физической точки зрения объяснить влияние параметра K на уровень флюктуационной и динамической составляющих ошибки САУ.
2. Как вычисляется дисперсия суммы 2-х коррелированных случайных процессов?
3. Какой порядок астатизма имеет исследуемая система (рис.3) по выходу y(t)? по выходу ε(t)?
4. Оценить влияние параметра K на дисперсию случайного процесса y(t), если на вход САУ поступает только экспоненциально-коррелированный процесс g(t). Чему равна дисперсия y(t) при неограниченном росте K?
5. Как отражается улучшение фильтрующих свойств системы на корреляционных свойствах флюктуационной ошибки?
6. Какой должна быть структура САУ, согласованной с формирующим фильтром данного макета?
8. Исследование нелинейной САУ
(лабораторная работа 7)*
Цель работы – ознакомление с практическим использованием методов гармонической и статистической линеаризации при анализе САУ, содержащей релейный элемент и инерционную линейную часть.
8.1. Описание лабораторной установки
Лабораторная установка содержит макет САУ, внешний генератор широкополосных случайных процессов и осциллограф. Исследуемая САУ (рис. 4) включает в себя нелинейный элемент типа реле с петлей гистерезиса и линейную часть, состоящую из электронного интегратора и цепей коррекции с функциями передачи z1(jω) и z2(jω).
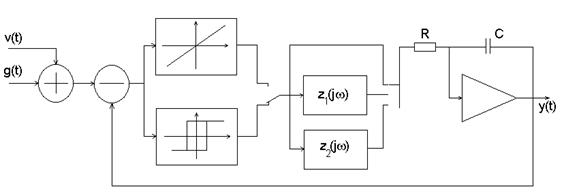
Рис.4
Схемы цепей коррекции и их параметры приведены на лабораторном макете. Нелинейный элемент может выключаться. На вход САУ можно подать скачкообразный сигнал g(t), а также широкополосный случайный процесс v(t) (с нулевым средним и спектральной плотностью мощности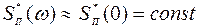 
). Уровень случайного процесса v(t) можно менять. Выходной сигнал y(t) контролируется с помощью осциллографа.
Метод гармонической линеаризации используется для анализа автоколебаний в нелинейной САУ. В ходе этого анализа необходимо ответить на следующие вопросы:
1) возможно ли возникновение автоколебаний в нелинейной САУ?
2) устойчив ли режим автоколебаний в случае их возникновения?
3) каковы параметры автоколебаний (амплитуда и частота)?
Условия возникновения автоколебаний в нелинейной САУ определяются решением уравнения замыкания
,
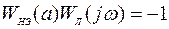где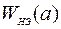 
- эквивалентная функция передачи нелинейного элемента;
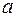- амплитуда 1-й гармоники на входе нелинейного элемента; 
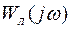- функция передачи линейной части системы.
Для исследуемого в макете САУ нелинейного элемента типа реле с петлей гистерезиса
,
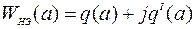где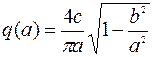 
; 
; 
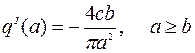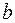и 
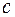- параметры нелинейного элемента, характеризующие размеры петли гистерезиса для входного и, соответственно, выходного процессов.
Эта функция передачи может быть представлена в виде
,
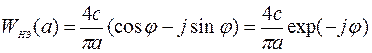где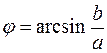 
. Такая запись показывает, что амплитуда 1-й гармоники на выходе реле с петлей гистерезиса такая же, как и на выходе идеального реле. Однако имеется фазовый сдвиг φ, обусловленный запаздыванием срабатывания такого реле в сравнении с идеальным.
Уравнение замыкания представляется в виде
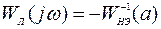
и решается графически. Для этой цели следует построить годограф Найквиста линейной части и годограф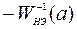 
нелинейного элемента. Наличие точки пересечения годографов является признаком возможности возникновения автоколебаний в нелинейной САУ. Устойчивость автоколебаний проверяется с помощью правила: режим автоколебаний в системе устойчив, если точка на годографе 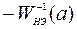, соответствующая увеличению амплитуды, не охватывается (в смысле критерия устойчивости Найквиста) годографом .
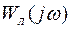Параметры автоколебаний (амплитуда и частота) определяются значениями соответствующих аргументов годографов в точке пересечения, однако для их определения необходимо иметь явную зависимость от аргументов функци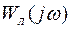й и 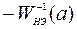. Параметры автоколебаний можно также определить экспериментально с помощью осциллографа.
Метод статистической линеаризации используется для анализа нелинейной САУ при воздействии на нее шума. При этом нелинейный элемент заменяется эквивалентным линейным элементом с двумя коэффициентами усиления: для регулярной составляющей сигнала (математического ожидания)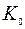 
и центрированной случайной составляющей сигнала 
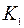. Для реле с петлей гистерезиса коэффициенты 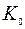и 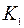определяются с помощью выражений
,
,
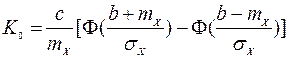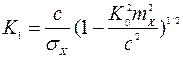где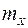 
и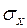 
- математическое ожидание (среднее) и среднеквадратичное значение сигнала на входе нелинейного элемента; 
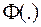- интеграл вероятности.
Так как коэффициент 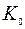зависит от 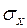, то и функция передачи линеаризованной САУ 
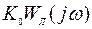зависит от уровня шума. Поэтому изменение 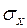влияет на свойства нелинейной САУ.
8.2. Задание по работе
1. Расчетная часть.
1) Построить ЛХ линейных САУ с различными цепями коррекции (значения параметров линейной части САУ указаны на лабораторном макете).
2) Построить годографы 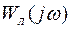и 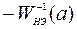нелинейных САУ с различными цепями коррекции и выполнить анализ автоколебаний. При построении годографа 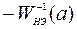следует учесть, что
,
.
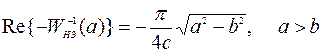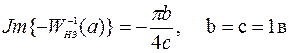3) Для различных значений 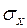построить семейство ЛХ линеаризованных САУ с различными цепями коррекции и функцией передачи 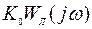. При вычислении коэффициента 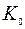использовать допущение 
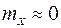(ошибка слежения в среднем близка к нулю), при котором громоздкое выражение для 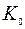можно упростить:
.
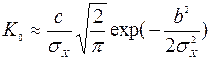Расчет 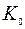выполнить для значений 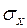, равных 
.
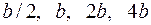2. Экспериментальная часть.
1) Подавая скачкообразное воздействие g(t), посмотреть на экране осциллографа и зарисовать переходные процессы линейных САУ 3-х типов (без коррекции и с цепями коррекции z1(jω) и z2(jω)). По степени колебательности переходных процессов оценить запас устойчивости по фазе.
2) Выполнить экспериментальный анализ автоколебаний в нелинейных САУ 3-х типов. Измерить частоту и амплитуду автоколебаний.
3) Для 3-х типов нелинейных САУ экспериментально исследовать срыв автоколебаний при изменении уровня шума на входе системы. Для этого следует постепенно увеличивать уровень шума до некоторого порогового уровня, при котором исчезает регулярная составляющая в выходном сигнале САУ (отсутствие регулярных автоколебаний свидетельствует о выполнении условий статистической линеаризации САУ). Пороговый уровень шума измерить.
4) Экспериментально исследовать влияние уровня шума на качество переходных процессов нелинейных САУ 3-х типов. Для этого установить уровень шума, соответствующий линеаризации САУ (срыв автоколебаний) и посмотреть несколько переходных процессов на экране осциллографа. Зарисовать усредненный (по ансамблю реализаций) переходный процесс. Затем увеличить уровень шума, снова посмотреть несколько реализаций переходного процесса, зарисовать усредненный процесс и сопоставить результаты. Уровни шума измерить с помощью осциллографа (при оценке 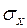процесс считать нормальным, не выходящим за пределы 
).
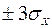5) Экспериментально оценить фильтрующие свойства линейных и нелинейных САУ 3-х типов.
8.3. Содержание отчета
1. Структурная схема макета САУ.