5. Построить АЧХ САУ 3-го типа для 3-х значений переменного резистора, включая оптимальное.
6.3. Содержание отчета
1. Функциональная схема лабораторного макета.
2. Функции передачи исследуемых САУ.
3. Результаты экспериментальных исследований переходных процессов САУ.
4. ЛХ исследуемых САУ.
5. Результаты экспериментальных исследований зависимости σШ от структуры и параметров САУ.
6. Семейство АЧХ для САУ 3-го типа.
6.4. Контрольные вопросы
1. Объяснить поведение σШ в САУ 1-го и 2-го типов.
2. Объяснить поведение σШ в САУ 3-го типа.
3. Объяснить поведение σШ в САУ 3-го типа при неограниченном росте значения переменного резистора.
4. Дать геометрическую и физическую интерпретацию эффективной полосы САУ.
5. Каков закон распределения вероятностей процесса на выходе САУ, если на входе он гауссовский?
6. Изобразить (качественно) закон распределения вероятностей случайного процесса на выходе измерителя среднеквадратического значения шумовой ошибки.
7. Параметрическая оптимизация САУ при наличии динамической и шумовой ошибок (лабораторная работа 6)*
Цель работы – практическое изучение возможности параметрической оптимизации САУ в установившемся режиме по критерию минимума среднего квадрата суммарной ошибки.
7.1. Описание лабораторной установки
Лабораторная установка включает в себя макет САУ, внешний генератор широкополосных случайных процессов и осциллограф.
Исследуемая САУ имеет функцию передачи в разомкнутом состоянии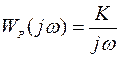 
. На вход САУ могут подаваться два случайных процесса: узкополосный g(t) (с нулевым средним и двусторонней спектральной плотностью мощности 
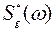и широкополосный v(t) (с нулевым средним и двусторонней спектральной плотностью мощности 
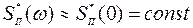). Процесс g(t) рассматривается как полезный сигнал, а процесс v(t) моделирует помеху в канале наблюдения g(t). Назначение САУ состоит в воспроизведении на выходе y(t) процесса g(t).
Ошибка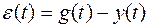 
воспроизведения процесса g(t) складывается из 2-х составляющих.
Первая составляющая обусловлена ошибкой воспроизведения процесса g(t) при отсутствии помехи v(t). Она зависит от динамики изменения процесса g(t), порядка астатизма и параметров САУ. Эту составляющую обычно называют динамической и дисперсию ее определяют с помощью выражения:
.
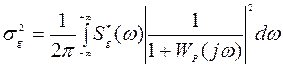Для экспоненциально-коррелированного случайного процесса g(t), получающегося в результате прохождения широкополосного случайного процесса (с нулевым средним и двусторонней спектральной плотностью мощности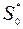 
) через апериодическое звено с функцией передачи 
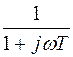, справедливо соотношение: 
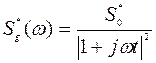. При этом дисперсия динамической составляющей ошибки САУ с функцией передачи 
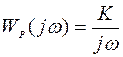равна
.
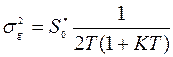Вторая составляющая ошибки воспроизведения процесса g(t) обусловлена воздействием только помехи v(t) и, поэтому, называется флюктуационной (шумовой). Дисперсия ее, в общем случае, определяется с помощью выражения
.
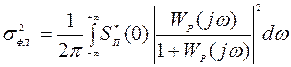Для САУ с функцией передачи 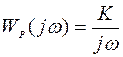дисперсия флюктуационной составляющей ошибки равна
.
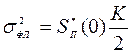Если случайные процессы g(t) и v(t) статистически независимы, то дисперсия суммарной ошибки равна
.
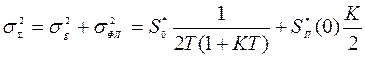С ростом единственного параметра САУ K первая составляющая суммарной ошибки уменьшается, а вторая увеличивается. При некотором значении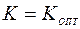 
имеет место минимум суммарной ошибки, а соответствующее значение 
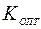является оптимальным. В случае известных 
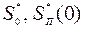и T значение 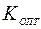легко найти из условия
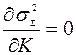. В рамках данной лабораторной работы значение 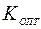определяется экспериментально.
Особенностью макета является формирование полезного сигнала g(t) c помощью v(t), что позволяет обойтись одним внешним генератором широкополосных случайных процессов. При этом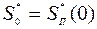 
, а выражение 
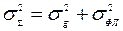неправомерно (условие статистической независимости g(t) и v(t) не выполняется. Для вычисления дисперсии 
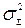в этом случае можно определить функцию передачи для суммарной ошибки системы, изображенной на рис.3, следующим образом. По структурной схеме составим систему уравнений
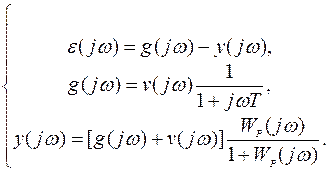
Далее определяем функцию передачи для суммарной ошибки системы, как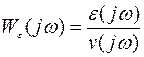 
и, методом исключения вспомогательных переменных, получаем
.
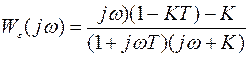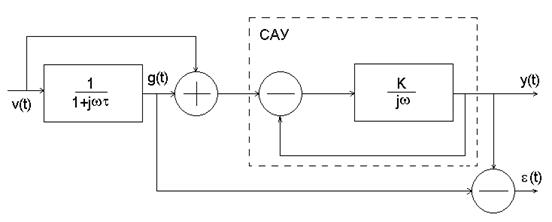
Рис.3
Остается вычислить дисперсию случайного процесса на выходе линейной системы с функцией передачи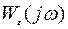 
:
.
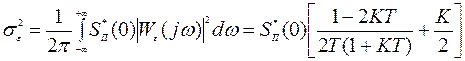Анализируя это выражение, нетрудно объяснить результат экспериментальных исследований, при котором дисперсия суммарной ошибки оказывается меньше дисперсий составляющих этой ошибки.
7.2. Задание по работе
1. Снять экспериментальные зависимости σg и σФЛ от параметра САУ K (для функции передачи электронного интегратора использовать аппроксимацию вида K/jω, где K определяется параметрами частотно-зависимой обратной связи операционного усилителя).
2. Снять экспериментальную зависимость σΣ от параметра САУ K и определить значение KОПТ.
3. Построить графики всех зависимостей в одних координатных осях.