1.2. Составление уравнений состояния электрической
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
1. ЛИНЕЙНЫЕ ЦЕПИ ПОСТОЯННОГО ТОКА
1.1. Основные топологические понятия
1.2. Составление уравнений состояния электрической
1.3. Методы контурных токов и узловых потенциалов
1.4. Пример расчета цепи постоянного тока
1.5. Задание для расчета (1 вариант)
1.6. Задание для расчета (2 вариант)
МИНИСТЕРСТВО ОБРАЗОВАНИЯ УКРАИНЫ
ПРИАЗОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
( ПГТУ)
Кафедра автоматизации электроэнергетические систем
( АЭС )
Леонов В.В.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ №1
по выполнению семестровых заданий»
по теоретическим основам электротехники
раздел "теория цепей"
(для студентов электротехнических специальностей)
Мариуполь 2004
УДК 621.3.01(075)
Сборник семестровых заданий по теоретическим основам электротехники. Раздел "Теория цепей" (для студентов электротехнических специальностей) / Составители В.В.Леонов, И.С.Кричман.
В данном пособии даны варианты семестровых заданий по теории электрических цепей и приводятся методические указания для их выполнения.
В пособии использованы материалы методических указаний профессора Л.А.Бессонова и доцента В.С.Зайцева.
Пособие предназначено для студентов электротехнических специальностей всех форм обучения, изучающих курс "Теоретические основы электротехники".
| В.Н.Кравченко |
Рецензент: доцент, канд.техн.наук
 |
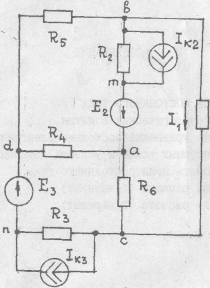
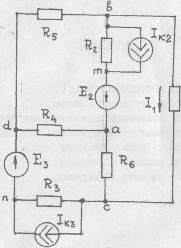
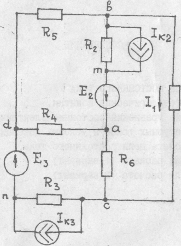
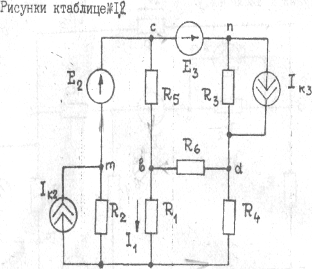
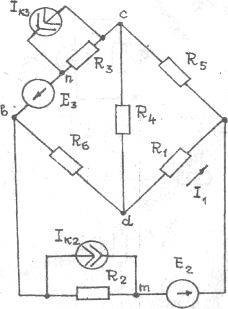
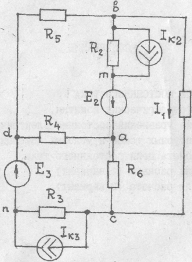
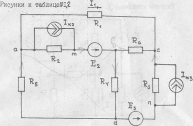
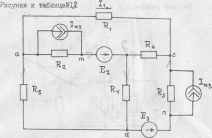
Рисунки к таблице №1.2
Рис.17
|
|
|
|
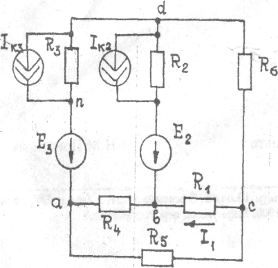
Рис.18
Рисунки к таблице №1.2
|
|
|
|
Рис.15
|
|
|
|
Рис..16
|
|
|
|
|
|
ВВЕДЕНИЕ
Выполнение семестровых заданий является основной формой самостоятельной работы студента над курсом теоретических основ электротехники. Именно в процессе работы над ними студент осваивает методы расчета электрических цепей и глубже понимает теоретический материал.
Семестровые задания охватывают основной материал раздела "Теория цепей". Они имеют 100 вариантов. Вариант определяется по номеру в журнале плюс задаваемое преподавателем число. В заданиях 1 и 2 имеются пункты, содержание которых определяется .первой буквой фамилии студента.
Для изучения курса и выполнения семестровых заданий рекомендуются учебники и учебные пособия, выпущенные в последние годы, однако можно использовать и более старые издания с учетом того, что в них может отсутствовать изложение некоторых вопросов. При использовании разных учебников необходимо учитывать, что ЭДС обозначают и буквой "Е", и "3", а потенциал «φ» и «U». В одних книгах положительное направление отсчета для напряжения между узлами или тачками схемы указывается с помощью индексов этих узлов или точек, в других -индексы узлов у напряжения не ставятся, а ставится стрелка и один индекс.
В качестве достаточно полного перечня вопросов для самопроверки могут служить названия параграфов в учебнике Л.А.Бессонова "Теоретические основы электротехники". Там же приведены задачи с решениями по всему разделу теории цепей. Для лучшего усвоения курса рекомендуется просмотреть решения этих задач. Немало решенных задач приводится в задачниках. Пособие предназначено для. студентов электротехнических специальностей всех форм обучения, изучающих курс "Теоретические основы электротехники".
При выполнении работ следует соблюдать следующие условия:
1) Семестровое задание сдается в виде сброшюрованной
расчетно-пояснительной записки. Формат бумаги - 285х205мм (до
пускается использование разворота листа школьной тетради).
2) Расчетно-пояснительная записка начинается с титульного листа (см. образец).
3)После титульного листа идет раздел "Задание",в котором отдельными строками излагаются исходные данные для выбранного варианта. Заданная принципиальная схема вычерчивается
для выбранного варианта.
4)После раздела "Задание " должен идти раздел "Решение", который делится на пункты в соответствии с пунктами задания. Каждый пункт начинается с подачи его содержания. Далее
приводятся расчетные формулы в общем виде, затем в них
подставляются данные и дается результат. Вывод известных из
курса формул не должен приводиться. Результат расчетов подается с указанием единиц измерения (по системе СИ). Содержащиеся в примерах указания и разъяснения приводить в тексте
расчетно-пояснительной записки не требуется.
5)Текст работы писать аккуратно, чернилами или постовой ручкой (исключительно синим, фиолетовым или черным цветом), оставляя поля для замечаний преподавателя и подшивки.
6)Вычерчивать схемы и векторные диаграммы карандашом с применением чертежных принадлежностей на отдельных листах.
7)Следует избегать графиков, в которых деление в начале координат начинается не с нулевого значения. Такие графики
не дают общего представления о характере зависимости. Разметка осей графиков должна выполняться черев равные интервалы
отражаемой величины.
8), Объем задания может быть сокращен по указанию преподавателя .
9) Записка должна быть подписана студентом.
Рисунки к таблице № 1.2
|
|
|
|
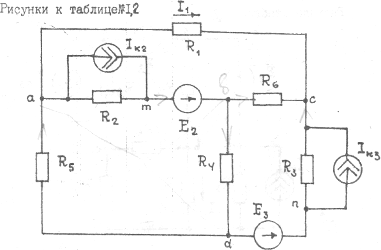
|
|
|
|
|
|
|
|
|
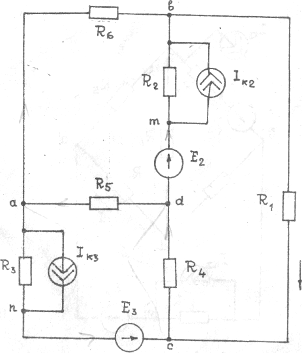 Рис.13
Рис.13
Рис .. 14
|
|
Рисунки к таблице № 1.2
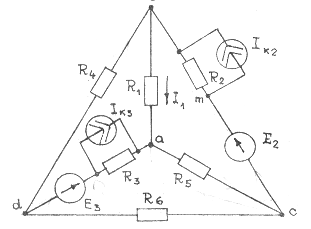 |
|
|
|
Рис.11
|
|
Рис..12
|
|
Образец титульного листа
Министерство образования Украины
Мариупольский металлургический институт
Кафедра электротехники и электрооборудования
Наименование работы
«РАСЧЁТ ЖНЕЙНЫХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА»
Вариант:……………
Срок сдачи а) по плану ……………
б) фактически…
ВЫПОЛНИЛ: студент группы Иванов И.И.
ПРОВЕРИЛ: доцент Леонов В.В.
Мариуполь 2004
1. ЛИНЕЙНЫЕ ЦЕПИ ПОСТОЯННОГО ТОКА 1.1. Основные топологические понятия
Электрическая цепь - совокупность устройств, образующих путь для тока. В электрической цепи осуществляется производство электрической энергии из других видов энергии, ее передача, распределение и преобразование в другие виды энергии. Отдельные устройства, составляющие электрическую цепь, называются элементами цепи. Основными элементами электрической цепи являются источники и приемники электрической энергии, соединенные между собой проводами или линиями передачи. В электрических цепях ток может быть постоянным (не изменяющимся во времени) или переменным (изменяющимся с течением времени), в связи с чем различают цепи постоянного тока и переменного тока.
Схема электрической цепи графическое изображение электрической цепи, содержащее условные обозначения ее элементов и показывающая их соединение. На схеме каждый элемент электрической цепи представлен его схемой замещения, состоящей из одного или нескольких элементов. Элементами схем электрически цепей постоянного тока (рис.11а) являются изображения резисторов R, называемые сопротивлениями или резистивными элементами, изображения источников ЭДС Е и изображения источников тока J.
Ветвь электрической цепи - участок электрической цепи, вдоль которого один и тот же ток. В схеме электрической цепи на рис.1.1,а шесть ветвей содержат резисторы и источники ЭДС (R1, Е1-Rб, Е6), две ветви - только резисторы (R7. R8) и две ветви - только источники тока (J1, J2).
Узел электрической цепи-места соединения ветвей электрической цепи. Обычно за узел принимают место соединения трех и более ветвей. Схема электрической цепи на рис.11,а содержит 5 узлов (отмечены цифрами в кружочках).
Контур электрической цепи - замкнутая непрерывность ветвей, в которой любой узел, кроме начального и конечного, встречаются только один раз.
Граф электрической схемы - изображение схемы электрической цепи, в которой ветви схемы представлены отрезками-ветвями
Рисунки к таблице № 1.1
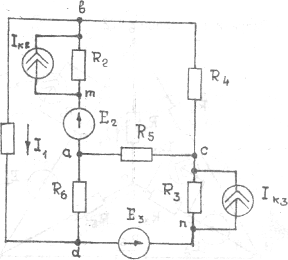 |
Рис.9
 |
Рис..10
Рисунки к таблице №1.2
Рис8.
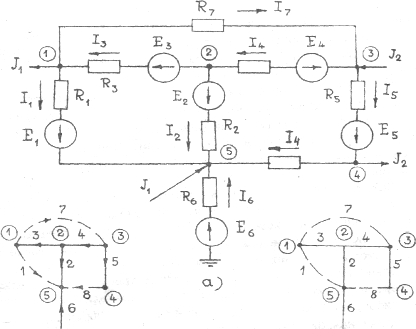
Рис.1.1.
графа, а узлы точками-узлами графа (рис.1.1,б). На графе не показывают ветви, которые которые не содержат источники тока и отнесенные к идеальным вольтметры. Нумерация ветвей графа соответствует нумерации токов ветвей электрической цепи.
Направленный (ориентированный) граф схемы - граф с указанной в виде стрелок ориентацией ветвей (рис.1.1,б). При отсутствии ориентации ветвей граф называют ненаправленным (неориентированным) графом схемы (рис.1.1,в). Направление ветвей графа выбирают совпадающим с принимаемым положительным направлением тока или напряжения ветвей схемы. Под напряжением ветви понимают напряжение между узлами схемы, к которым присоединена ветвь. Выбираем произвольно положительные направления тока и напряжения ветви схемы принимаются совпадающими.
Дерево графа схемы - любая совокупность ветвей графа, соединяющих его узлы без образования контуров. Ветви графа, образующие дерево, называются ветвями дерева. Ветви графа, дополняющие дерево до исходного графа, называют ветвями связи.
На рис. 1.1,б,в ветви одного из возможных деревьев графа показаны сплошными линиями, а ветви связи - штриховыми линиями. Контур, образованный из ветвей дерева и только одной ветви связи, называют главным контуром.
В теории электрических цепей под расчетом электрической цепи в общем случае понимают определение токов ветвей по заданным значениям сопротивлений резисторов, ЭДС источников напряжения и токов источников тока. Систему уравнений, позволяющих рассчитать электрическую цепь, называют уравнением состояния.
Как очевидно, к расчетному числу токов, подлежащих определению, не относятся токи ветвей, содержащих источники тока, поскольку они равны токам этих источников. Следовательно, расчетное количество токов равно числу ветвей графа электрической схемы, которое называют расчетным числом ветвей схемы.
Возможны также задачи, в которых требуется определить, например, значения ЭДС каких-либо источников или сопротивления каких-либо резисторов электрической цепи. Для разрешимости этой задачи каждой такой искомой величине должен соответствовать в исходных данных известный ток какой-либо ветви, поскольку число неизвестных величин должно быть равно расчетному числу ветвей схемы.
Для упрощения расчетов не рекомендуется относить к расчетному числу те ветви, которые не содержат ни пассивных, ни' активных элементов. В расчетное число ветвей не включают также ветви электрической цепи, в которых ток заведомо равен нулю.
1.2. Составление уравнений состояния электрической цепи по законам Кирхгофа
Согласно первому закону Кирхгофа, применяемому к узлам цепи, в любом узле электрической цепи алгебраическая сумма токов равна нулю, т.е.
∑ Ik - О. (1.1)
Условимся записывать в уравнениях токи, направленные от рассматриваемого узла, с положительным знаком, а токи, направленные к узлу, с отрицательным знаком.
В уравнения (1.1) входят также токи источника ока, которые присоединены к узлу. В том случае, когда токи источника
Рисунки к таблице № 1.2.
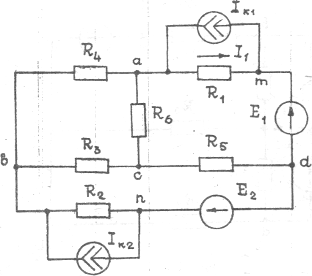 |
Рис.5
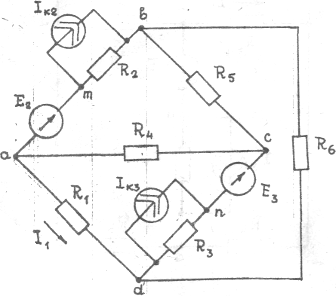
Рис..6
Рисунки к таблице №1.2
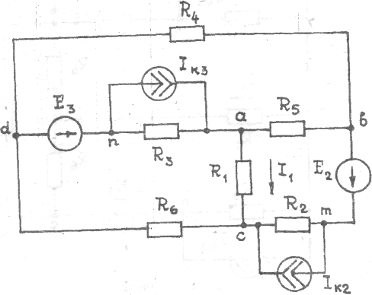 |
Рис.3
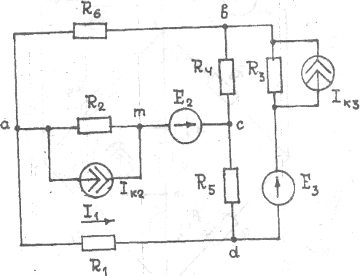 |
Рис..4
тока известны, целесообразно записывать их в правой части уравнений
∑ Ik - ∑Jk. (1.2)
изменив для них правило знаков на противоположное указанному.
Число независимых уравнений, составляемых по1 закону Кирхгофа для расчета электрической цепи, К1 - У - 1, где У -количество узлов схемы. Узлы, соответствующие этим уравнениям, также называют независимыми.
Согласно второму закону Кирхгофа, применяемому к контурам цепи, в любом контуре электрической цепи алгебраическая сумма напряжений ветвей или напряжений на элементах равна нулю, т.е.
∑Uk - 0. (1.3)
С положительным знаком записываются напряжения, направление которых совпадает с произвольно выбранным направлением обхода контура, а напряжения, встречные направлению обхода контура, записываются со знаком минус.
В уравнения (1.3), составленные для напряжений на элементах цепи, кроме напряжений на резисторах, входят напряжения источников ЭДС, которые обычно известны. Поэтому целесообразно значения ЭДС источников записывать в правой части уравнений
∑ Rk Ik - ∑ Ek (1.4)
Здесь знак плюс принимают для тех токов и ЭДС, положительное направление которых совпадает с направлением обхода контура.
Число независимых уравнений, составляемых по закону Кирхгофа для расчета цепи, К2 - В – К1 - В - (У - 1), где В -расчетное количество ветвей схемы. Контуры, соответствующие этим уравнениям, также называют независимыми. Выделить независимые контуры электрической цепи можно по графу схемы. Как видно из рис.11б, число ветвей дерева Кд - У - 1, а число ветвей связи Кс = В - Кд = В - (У - 1) = К2. Каждой ветви связи соответствует главный контур. Таким образом, главные контуры и составленные для них уравнения являются независимыми, их число равно требуемому.
Составление системы уравнений по законам Кирхгофа рассмотрим на примере схемы рис,1.1: полагая известными значения сопротивлений R1-R5, R7, R8, ЭДС Е1 - Е5 и токов J1, J2. Произвольно принятые положительные направления искомых токов
I1- I7 показаны на схеме стрелками.
Схема содержит 7 ветвей и 5 узлов. Следовательно, независимыми уравнениями, составленными по первому закону Кирхгофа, будут К1 - У - 1 - 4 уравнения; составленными по второму закону Кирхгофа К2-В-(У-1)-3 уравнения. Всего должно быть составлено К - К1 + К2 - 7 уравнений, которые позволят определить 7 искомых токов.
1.3. Методы контурных токов и узловых потенциалов
С целью сокращения числа совместно решаемых алгебраических уравнений применяют для расчета электрических цепей методы контурных токов или узловых потенциалов.
Метод контурных токов основан на применении второго закона Кирхгофа, поэтому количество составляемых уравнений равно числу независимых контуров электрической цепи. Согласно этому методу полагают, что в каждом независимом контуре замыкается так называемый контурный ток, положительное направление которого выбирают произвольно. При наличии в цепи источников тока вводят дополнительно контурные токи, замыкающиеся через каждый такой источник по любому пути в схеме. Эти дополнительные контурные .токи равны токам тех источников, через которые они замыкаются. Уравнения составляют только для независимых контуров, пользуясь правилом второго закона Кирхгофа: алгебраическая сумма падений напряжений на всех резисторах, принадлежащих контуру, от всех без исключения контурных токов, которые по ним проходят, равна алгебраической сумме ЭДС источников, содержащихся в рассматриваемом контуре. Каждый контур обходят по направлению его контурного тока.
Метод узловых потенциалов основан на применении первого закона Кирхгофа и обобщенного закона Ома, в следствии чего количество составляемых уравнений равно числу независимых узлов электрической цепи. Согласно этому методу потенциал одного ив узлов, называемого базисным, принимают равным нулю. Для нахождения потенциалов остальных узлов составляют уравнения применительно к каждому из них.
Рисунки к таблице № 12
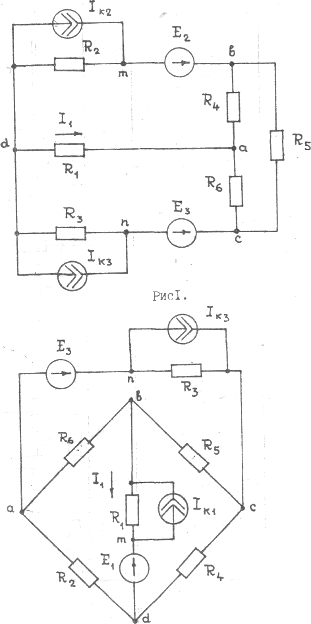 |
Рис.2
Продолжение таблицы 1.2.
| N | Рисунок | Rl | R2 | R3 | R4 | R5 | R6 | El | E 2 | E 3 | J 1 | J2 | J3 |
| O м | В | А | |||||||||||
| 51 | 9 | 3,5 | 6 | 2 | 4,5 | 7,5 | 4 | 7 | 5 | 0,5 | 0 | ||
| 52 | 18 | 15 | 20 | 11 | 5 | 7 | 25 | 7,5 | 7,5 | 0,2 | 0 | ||
| 53 | 12 | 7,5 | 6 | 5 | 4,5 | 4 | 3,5 | 3,5 | 10 | 0,4 | 0 | ||
| 54 | 4 | 6 | 17,5 | 11 | 3 | 5 | 7,5 | 6,5 | 6 | 0,2 | 0 | ||
| 55 | 13 | 2 | 3,5 | 5 | 6 | 10 | 2,75 | 6,5 | 10 | 1 | 0 | ||
| 56 | 5 | 2 | 5,5 | 2.5 | 6 | 3,5 | 4 | 10,5 | 5 | 1 | 0 | ||
| 57 | 14 | 4,5 | 10 | 8 | 20 | 15 | 11 | 10 | 9 | 0,5 | 0 | ||
| 58 | 6 | 2,5 | 5 | 6 | 3,5 | 4 | 7,5 | 6 | 12,5 | 0,3 | 0 | ||
| 59 | 17 | 2,5 | 3,5 | 5 | 2 | 7,5 | 10 | 7 | 15 | 0,2 | 0 | ||
| 60 | 2 | 4 | 6 | 3 | 7,5 | 10,5 | 13 | 10,5 | 10 | 0,5 | 0 | ||
| 61 | 15 | 26 | 10 | 18 | 14 | 20 | 8 | 20 | 24 | 0 | 2 | ||
| 62 | 1 | 26 | 10 | 4 | 16 | 22 | 30 | 24 | 32 | 0 | 2 | ||
| 63 | 16 | 8 | 16 | 12 | 20 | 26 | 20 | 60 | 24 | 0 | 0,5 | ||
| 64 | 11 | 40 | 160 | 200 | 70 | 300 | 80 | 200 | 200 | 0 | 1,5 | ||
| 65 | 17 | 20 | 36 | 10 | 20 | 16 | 12 | 40 | 40 | 0 | 3 | ||
| 66 | 3 | 8 | 26 | 18 | 20 | 10 | 12 | 32 | 11 | 0 | 0,5 | ||
| 67 | 7 | 260 | 80 | 120 | 160 | 220 | 90 | 24 | 34 | 0 | 0.2 | ||
| 68 | 10 | 12 | 10 | 16 | 28 | 14 | 16 | 40 | 12 | 0 | 2 | ||
| 69 | 8 | 110 | 160 | 200 | 80 | 140 | 240 | 50 | 22 | 0 | 0,04 | ||
| 70 | 10 | 220 | 120 | 90 | 300 | 160 | 100 | 50 | 22 | 0 | 0,05 | ||
| 71 | 9 | 14 | 24 | 8 | 18 | 30 | 16 | 40 | 12 | 0 | 1 | ||
| 72 | 18 | 60 | 80 | 44 | 20 | 28 | 100 | 46 | 8 | 0 | 0,5 | ||
| 73 | 12 | 30 | 24 | 20 | 18 | 16 | 14 | 26 | 28 | 0 | 0,5 | ||
| 74 | 4 | 24 | 70 | 44 | 12 | 20 | 30 | 40 | 19,6 | 0 | 0,1 | ||
| 75 | 13 | 8 | 14 | 20 | 24 | 40 | 11 | 40 | 10 | 0 | 1,5 | ||
| 76 | 5 | 8 | 22 | 10 | 24 | 14 | 16 | 50 | 16,6 | 0 | 0,2 | ||
| 77 | 14 | 18 | 40 | 32 | 80 | 60 | 44 | 60 | 28 | 0 | 0,25 | ||
| 78 | 6 | 10 | 20 | 24 | 14 | 16 | 30 | 30 | 38 | 0 | 0,5 | ||
| 79 | 14 | 10 | 14 | 20 | 8 | 30 | 40 | 30 | 20 | 0 | 2 | ||
| 80 | 2 | 16 | 20 | 12 | 30 | 42 | 52 | 50 | 34 | 0 | 0,5 | ||
| 81 | 15 | 32,5 | 12,5 | 22,5 | 17,5 | 25 | 10 | 20 | 75 | 0,4 | 0 и | ||
| 82 | 1 | 32,5 | 12,5 | 5 | 20 | 27,5 | 37,5 | 25 | 50 | 0,4 | 0 | ||
| 83 | 16 | 10 | 20 | 15 | 25 | 32,5 | 25 | 35 | 37,5 | 2 | 0 | ||
| 84 | 11 | 50 | 200 | 250 | 87 | 375 | 100 | 150 | 625 | 0,5 | 0 | ||
| 85 | 17 | 25 | 45 | 12,5 | 25 | 20 | 15 | 32 | 87,5 | 0,4 | 0 | ||
| 86 | 3 | 10 | 32,5 | 22,5 | 25 | 12,5 | 15 | 27 | 25 | 0,4 | 0 | ||
| 87 | 7 | 325 | 100 | 150 | 200 | 275 | 112 | 17 | 62,5 | 0,04 | 0 | 0 | |
| 88 | 10 | 15 | 12,5 | 20 | 35 | 17,5 | 20 | 25 | 55 | 2 | 0 | ||
| 89 | 8 | 137 | 200 | 250 | 100 | 175 | 300 | 34,5 | 37,5 | 0,14 | 0 | ||
| 90 | 10 | 275 | 150 | 112 | 375 | 200 | 225 | 24 | 35 | 0,14 | 0 | ||
| 91 | 9 | 17,5 | 30 | 10 | 22,5 | 37,5 | 20 | 26 | 25 | 0,8 | 0 | ||
| 92 | 18 | 75 | 100 | 55 | 25 | 35 | 125 | 32,5 | 37,5 | 0,25 | 0 | ||
| 93 | 12 | 37,5 | 30 | 25 | 22,5 | 20 | 17,5 | 25 | 50 | 0,2 | 0 | ||
| 94 | 4 | 30 | 87,5 | 55 | 15 | 25 | 37,5 | 15 | 30 | 0,4 | 0 | ||
| 95 | 13 | 10 | 17,5 | 25 | 30 | 50 | 137,5 | 15 | 50 | 2 | 0 | ||
| 96 | 5 | 10 | 27,5 | 12,5 | 30 | 17,5 | 20 | 32,5 | 25 | 3 | 0 | ||
| 97 | 14 | 22,5 | 50 | 40 | 100 | 75 | 55 | 35 | 45 | 0,8 | 0 | ||
| 98 | 6 | 12,5 | 25 | 30 | 17,5 | 20 | 37,5 | 35 | 62,5 | 0,1 | 0 | ||
| 99 | 16 | 12,5 | 17,5 | 25 | 10 | 37,5 | 50 | 30 | 75 | 0,6 | 0 | ||
| 100 | 2 | 20 | 25 | 15 | 37,5 | 52,5 | 65 | 50,5 | 50 | 0,6 | 0 |
1.4. Пример расчета цепи постоянного тока
В процессе работы над заданием, необходимо выполнить
следующее;
1) Составить на основании законов Кирхгофа систему
уравнений для расчета токов во всех ветвях схемы.
2) Определить токи во всех ветвях схемы методом контурных токов,
3) Определить токи во всех ветвях схемы методом узловых
потенциалов,
4) Результаты расчета токов, проведенного двумя метода
ми, свести в таблицу и сравнить между собой.
5) Составить баланс мощностей в исходной схеме (схеме с
источником тока), вычислив суммарную мощность источников и
суммарную мощность нагрузок (сопротивлений).
6) Определить ток Ц в заданной схеме с источником тока, используя метод эквивалентного генератора.
7)Начертить потенциальную диаграмму для любого замкну
того контура, включающего обе ЭДС
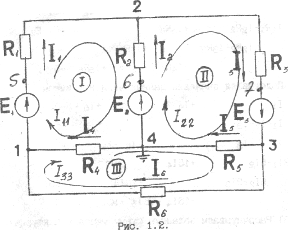
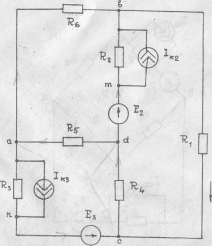
Рис.1.2.
Дано: E=20В; Е2=15В; Е3=50В
R1=3Ом; R2=5Ом; R3=2Ом;
R4=15Ом; R5=20Ом; R6=10Ом.
Решение.
1)Задаемся произвольно направлениями токов в ветвях.
2)Составляем систему уравнений расчета токов в ветвях.
Поскольку неизвестны шесть токов , система должна содержать
шесть уравнений. Сначала составляем уравнения, основанные на
первом законе Кирхгофа, затем составляем уравнения на основа
нии второго закона Кирхгофа. Так как в заданной схеме 4 узла,
на основании первого закона Кирхгофа может быть составлено три
независимых уравнения (выбираем узлы 1,2,3).
Недостающие 3 уравнения составляют для независимых контуров I, II, III (направление обхода выбираем по часовой стрелке).
Система уравнений записывается в виде, удобном для решения матричным методом.
-I1 +I4 +I6 -0;
I1+I2-I3 -0;
I3 -I5 -I6 -0;
I1R1-I2R2 +I4R4 -E1-E2
I2R2+I3R3 +I5R5 -E2+E3
-I4R4 –I5R5 +I6R6 -0
Подставляя значения данных величин, имеем:
-I1 +I4 +I6 -0;
I1+I2-I3 -0;
I3 -I5 –I6 -0;
3I1-5I2 +20I5 -65;
-15I4 -20I5+I6 -0.
3) Рассчитываем заданную схему методом контурных токов.
Выбираем произвольно направление контурных токов 1ц, 122» 1зз
(Рис.1.2).
Система уравнений для схемы , содержащей 3 контура , в общем
Таблица 1. 2.
| N | Рисунок | R1 | R2 | R3 | R4 | R5 | R6 | E1 | Е2 | E3 | J1 | J2 | J3 |
| Oм | в | А | |||||||||||
| 1 | 15 | 13 | 5 | 9 | 7 | 10 | 4 | 10 | 21 | 0 | 1 | ||
| 2 | 1 | 13 | 5 | 2 | 8 | 11 | 15 | 12 | 16 | 0 | 2 | ||
| 3 | 16 | 4 | 8 | 6 | 10 | 13 | 10 | 30 | 9 | 0 | 1 Л. 1 | ||
| 4 | 11 | 20 | 80 | 100 | 35 | 150 | 40 | 100 | 150 | 0 | 1 | ||
| 5 | 17 | 10 | 18 | 5 | 10 | 8 | 6 | 20 | 30 | 0 | 1 | ||
| 6 | 3 | 4 | 13 | 9 | 10 | 15 | 6 | 16 | 8,2 | 0 | 0,2 | ||
| 7 | 7 | 130 | 40 | 60 | 80 | 110 | 45 | 12 | 13 | 0 | 0,3 | ||
| 8 | 30 | 6 | 5 | 3 | 14 | 7 | 8 | 20 | 14 | 0 | 1 | ||
| 9 | 8 | 55 | 80 | 100 | 40 | 70 | 120 | 25 | 10 | 0 | 0,05 | ||
| 10 | 10 | 110 | 60 | 45 | 150 | 80 | 50 | 10 | 8 | 0 | 0,1 | ||
| 11 | 9 | 7 | 12 | 4 | 9 | 15 | 8 | 20 | 8 | 0 | 0,5 | ||
| 12 | 18 | 30 | 40 | 22 | 10 | 14 | 50 | 23 | 9,5 | 0 | 0,25 | ||
| 13 | 12 | 15 | 12 | 10 | 9 | 8 | 7 | 13 | 14 | 0 | 0,5 | ||
| 14 | 4 | 12 | 35 | 22 | 6 | 10 | 15 | 20 | 7,6 | 0 | 0,2 | ||
| 15 | 13 | 4 | 7 | 10 | 12 | 20 | 5,5 | 20 | 10 | 0 | 1 | ||
| 16 | 5 | 4 | 11 | 5 | 12 | 7 | 8 | 25 | 4,5 | 0 | 0,5 | ||
| 17 | 14 | 9 | 20 | 16 | 40 | 30 | 22 | 30 | 10 | 0 | 0,5 | ||
| 18 | 6 | 5 | 10 | 12 | 7 | 8 | 15 | 15 | 13 | 0 | 1 | ||
| 19 | 18 | 5 | 7 | 10 | 4 | 15 | 20 | 15 | 20 | 0 | 1 | ||
| 20 | 2 | 8 | 10 | 6 | 15 | 21 | 26 | 25 | 14 | 0 | 1 | ||
| 21 | 15 | 19,5 | 7,5 | 13,5 | 10,5 | 15 | 6 | 9 | 45 | 0,8 | 0 | ||
| 22 | 1 | 91,5 | 7,5 | 3 | 12 | 16,5 | 22,5 | 12 | 30 | 0.8 | 0 | ||
| 23 | 16 | 6 | 12 | 9 | 15 | 19,5 | 15 | 21 | 22,5 | 2 | 0 | ||
| 24 | 11 | 30 | 120 | 150 | 52,5 | 225 | 60 | 90 375 | 0.5 | 0 | |||
| 25 | 17 | 15 | 27 | 7,5 | 15 | 12 | 9 | 16,5 | 52.5 | 0.5 | 0 | ||
| 26 | 3 | 6 | 19,5 | 13,5 | 15 | 7,5 | 9 | 16,2 | 15 | 0,4 | 0 | ||
| 27 | 7 | 195 | 60 | 96 | 120 | 165 | 67,5 | 10,2 | 37,5 | 0,04 | 0 | ||
| 28 | 10 | 9 | 7,5 | 12 | 21 | 10,5 | 12 | 15 | 33 | 2 | 0 | ||
| 29 | 8 | 82,5 | 120 | 150 | 60 | 105 | 180 | 22,5 | 22,5 | 0,1 | 0 | ||
| 30 | 10 | 165 | 90 | 67,5 | 225 | 120 | 75 | 21 | 21 | 0,1 | 0 | ||
| 31 | 9 | 10,5 | 18 | 5 | 13, 5 | 22,5 | 12 | 12 | 15 | 1 | 0 | ||
| 32 | 18 | 45 | 60 | 33 | 15 | 21 | 75 | 16,5 | 22,5 | 0,3 | 0 | ||
| 33 | 12 | 22,5 | 18 | 15 | 13.5 | 12 | 10,5 | 15 | 30 | 0,2 | 0 | ||
| 34 | 4 | 18 | 52,5 | 33 | 9 | 15 | 22,5 | 9 | 18 | 0,4 | 0 | ||
| 35 | 13 | 6 | 10,5 | 15 | 18 | 30 | 8,25 | 9 | 30 | 2 | 0 | ||
| 36 | 5 | 6 | 16,5 | 7,5 | 18 | 10,5 | 12 | 25,5 | 15 | 2 | 0 | ||
| 37 | 14 | 13,5 | 30 | 24 | 60 | 45 | 33 | 15 | 27 | 1 | 0 | ||
| 38 | 6 | 7,5 | 15 | 18 | 10,5 | 12 | 22,5 | 15 | 37,5 | 0,5 | 0 | ||
| 39 | 16 | 7,5 | 10,5 | 15 | 6 | 22,5 | 30 | 15 | 45 | 1 | 0 | ||
| 40 | 2 | 12 | 15 | 9 | 22,5 | 31,5 | 39 | 25,5 | 30 | 1 | 0 | ||
| 41 | 15 | 6,5 | 2,5 | 4.5 | 3,5 | 5 | 2 | 4 | 15 | 0,4 | 0 | ||
| 42 | 1 | 6,5 | 2,5 | 1 | 4 | 5,5 и « и) | 7,5 | 5 | 10 | 0,4 | 0 | ||
| 43 | 16 | 2 | 4 | 3 | 5 | 6,5 | 5 | 11 | 7,5 | 1 | 0 | ||
| 44 | 11 | 10 | 40 | 50 | 17,5 | 75 | 20 | 34 | 125 | 0,4 | 0 | ||
| 45 | 17 | 5 | 9 | 2,5 | 5 | 4 | 3 | 8,2 | 17,5 | 0,2 | 0 | ||
| 46 | 3 С | 2 | 6,5 | 5 | 2,5 | 3 | 6,7 | 5 | 0,2 | 0 | |||
| 47 | 7 | 65 | 26 | 30 | 40 | 55 | 22,5 | 4,7 | 12,5 | 0,02 | 0 | ||
| 48 | 10 | 3 | 2,5 | 4 | 7 | 3,5 | 4 | 7,5 | 11 | 1 | 0 | ||
| 49 | 8 | 27,5 | 40 | 50 | 20 | 35 | 60 | 6,5 | 7,5 | 0,15 | 0 | ||
| 50 | 10 | 55 | 30 | 22,5 | 75 | 40 | 25 | 8,1 | 7 | 0,08 | 0 | ||
1.6. Задание для расчета (2 вариант)
Величины сопротивлений, ЭДС, И токов источника топа для каждого варианта даны в табл.1.2.
Указания:
1)Ответвления к источнику тока, ток которого по условию равен нулю, на схемах не показывать.
2)Обозначая на схеме токи в ветвях, необходимо учесть,
что ток через сопротивление/ параллельное источнику тока, от
личается от тока источника тока и тока через источник ЭДС.
3)Перед выполнением пп. 2 и 3 рекомендуется преобразовать источник -тока в источник ЭДС и вести расчет для получен
ной схемы.
4)В п. б при определении входного сопротивления двухполюсника следует преобразовать схему соединения треугольником
в эквивалентную схему соединения звездой.
Указания к выбору варианта в пп. 3 и 7:
Для студентов фамилии которых начинаются с букв А-Е, а нулевой потенциал принять потенциал узла а; с букв Ж-М - потенциал узла b; с букв Н-Т - потенциал узла с; с букв У-Я -потенциал узла д..
5) При отсутствии в строке величины, списывать ближайшее значение вверху или внизу
виде имеет следующий вид
R11 I11 + R12 I22 + R13 I33 = E11;
R21 I11 + R22 I22 + R23 I33 = E22; (1.7)
R31 I11 + R32 I22 + R33 I33 = E33;
или в матричной форме: │R│ │I│-│E│
где
| R11 | R12 | R13 |
| R12 | R22 | R23 |
| R13 | R32 | R33 |
| I11 |
| I12 |
| I13 |
| E11 |
| E22 |
| E33 |
│R│=-│I│= │E│=
Контурный ток Ikk равен
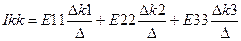 (1.8)
(1.8)
В уравнении (1.8) Δ – определитель системы:
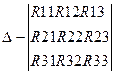
Δkm – алгебраическое дополнение, полученное из путем вычеркивания К-го столбца и m-той строки и умножения полученного определителя на 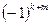
Так как определитель симметричен относительно главной диагонали, то
Δ km – Δ mk.
Решение системы (1.7) может быть найдено также в виде
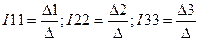
Здесь Δ1 получается из путем замены первого столбца на столбец │E│ правой части уравнения (1.7), Δ2 получаем путем замены второго столбца на │E│из Δ3 получается путем замены третьего столбца на столбец правых частей уравнений (1.7).
Определим величины элементов, входящих в матрицы R и E:
R11 = R1 + R2 + R4 – 3 + 5 + 15 = 23Om;
R22 = R1 + R2 + R5 – 5 + 3 + 20 = 28Om;
R33 = R4 + R5 + R6 – 15 + 20 + 10 = 45Om;
R12 = R21 – R2 = - 5Om.
R13 = R31 = - R4 = – 15Om;
R23 = R32 = – R5 = – 20Om;
E11 = E1 – E2 = 20 – 15 = 5B;
E22 – E2+E3 – 15 + 50 – 65B;
E33 = 0.
Система уравнений (1.7) запишется в виде
25 I11 – 5 I22 – 5 I33 = 5
-5 I11 + 28 I22 – 20 I33 = 65 (1.10)
-15 I11 – 20 I22 + 45 I33 = 0
Решение системы (1.10) необходимо осуществлять с помощью ЭВМ, для которых имеются соответствующие программы.
Решение системы (1.10) дает значения для контурных токов:
I11 = 4.470A; I22 = 6.469A; I33 = 4.365A.
В соответствии с рис. 1.2. искомые точки в ветвях определяются как:
I1 = I11; I2 = I22 – I11; I3 = I22; I4 = I11 – I33;
I5 = I22 – I33; I6 = I33;
I1 = 4.47A; I2 = 1.999A; I3 = 6.469A;
I4 = 0.105A; I5 = 2.104A; I6 = 4.365A.
Если в результате расчетов какой-либо ток окажется отрицательным, это означает, что действительное направление ток обратно принятому на рис. 1.2.
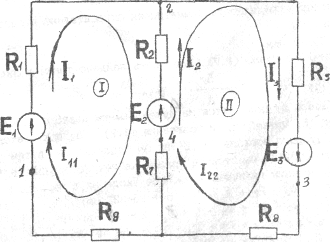
Рис.1.3.
Рисунки к таблице 1.1
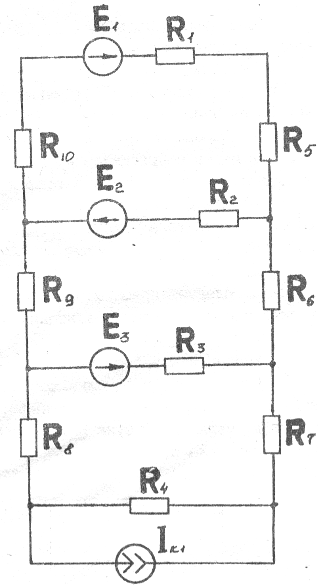
Рис.7
Рисунки к табл. 1. 1.
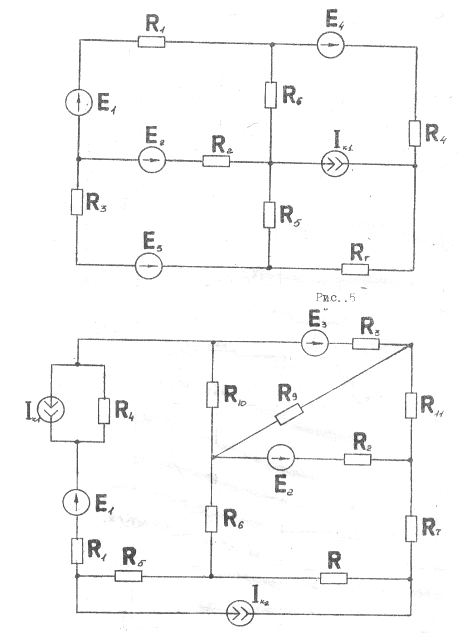
Рис.6
Замечания:
1) Расчет схемы рис.1.2. можно несколько упростить, преобразовав треугольник сопротивлений R4, R5, R6 в звезду.
В этом случае схема рис. 1.2. примет вид, показаний на рис. 1.3
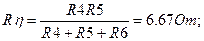
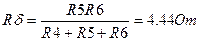 ;
;
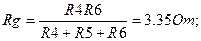
После расчета схемы рис. 1.3. токи в сопротивлениях R4, R5, R6 находятся из условия, что разности потенциалов U41, U34, U31 в схемах рис. 1.2 и рис. 1.3 одинаковы.
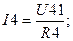
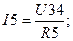
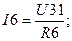
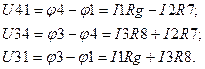
При расчете схемы рис 1.3. решается система из 2-х уравнений, так как схема содержит 2 независимых контура.
2) Если в схеме имеются источники тока, допускается их замена на источник Э.Д.С. Если такая замена затруднена, то выделяется контур с источником тока, причем контурный ток в этом контуре удобно принять равным току источника тока.
3) Рассчитываем схему (рис.1.2.) методом узловых потенциалов. Примем потенциал узла «4» равным 0. φ4 – 0.
Система уравнений, описывающих схему, в общем виде имеет вид:
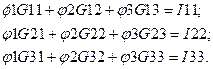
Система (1.11) решается аналогично системе (1.7). Определим коэффициенты и свободные члены в уравнениях системы (1.11).
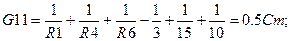
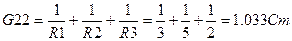
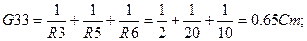
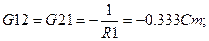
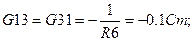
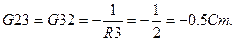
Узловые токи:
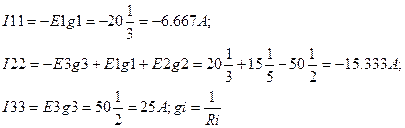
Система уравнений (1.11) примет вид:
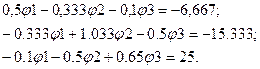
Зная потенциалы узлов φ1, φ2, φ3 и φ4 определяем токи в ветвях, для чего используем закон Ома в т.ч. для ветвей, содержащих Э.Д.С.:
φ1 + E1 – I1R1 = φ2; I1 = (E1+U12) = g1; U12 = φ1 – φ2;
g1= 1/R1
Аналогично: I2 = (E2 + U42) g2; I3 = (E3 + U23) g3;
I4 = U41 g4; I5 = U34 g5; I6 = U31 g6.
При расчетах учитывается, что φ4 = 0.
В рассматриваемом примере:
I1 = -4.466A; I2 = 1.998A; I3 = 6.17A;
I4 = 0.1053A; I5 = 2.133A; I6 = 4.42A.
Рисунки к таблице 1.1.
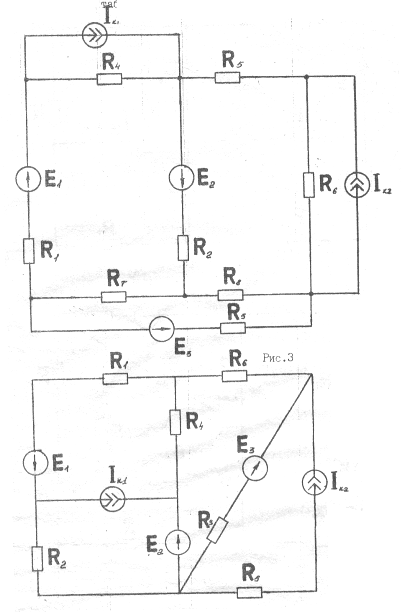
Рис.4
Рисунки к таблице №1.1
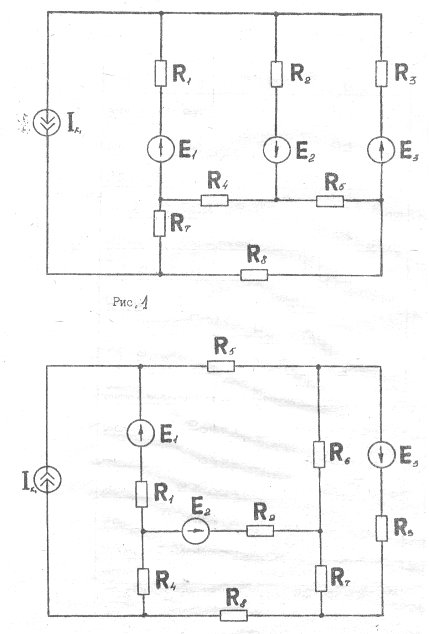
Рис.2
Разница в величинах токов, подсчитанных методами контур-
ных токов и узловых потенциалов, незначительна. Погрешность в расчетах составляет около 1%.
5) Определим ток в сопротивлении Rб методом эквивалентного генератора. В соответствии с этим методом искомый ток определится, как
I6 = U31xx / Rвх + R6
где U31xx - напряжение между узлами 3 и 1 при отброшенной ветви с сопротивлением R6;
Rвх - сопротивление относительно зажимов 3 и 1.
На рис. 1.4 приведена схема для определения U31xx
2
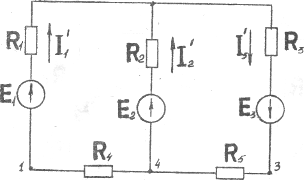
Рис. 1.4.
Применяя метод двух узлов, имеем
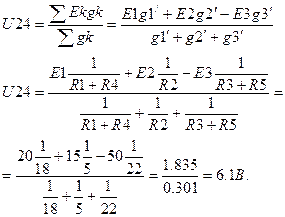
Ток I1´ = (E1 – U24)g1´ = (20 – 6.1) = 1/18 = 0.773A;
Ток I3´ = (E3 + U24)g3´ = (50 + 6.1) = 1/22 = 2.55A;
Ток I2´ = (E2 – U24)g2´ = (15 – 6.1) = 1/5 = 1.78A;
U31xx = I3´ R5 + I1´ R4 = 2.55 · 20 + 0.773 · 1/5 = 62.7B.
Входное сопротивление Rвх определяется относительно зажимов 1 и 3 при закороченных Э.Д.С. (и при разомкнутых источниках тока, если они смеются в схеме).
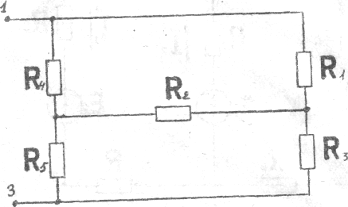 |
Рис.1.5.
Для определения Rвх удобно изобразить рассматриваемую схему так, как это показано на рис.1.5.
Преобразуем треугольник сопротивлений R4, R2, R1 в эквивалентную звезду (рис.1.6.).
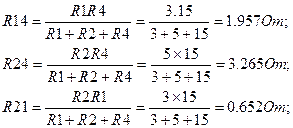
Тогда
|
|
| R11 |
| - - - - - 22 - - - - - - 22 - - - - - - 15 - - - - - - 15 - |
| R10 | - - - - - 18 20 - - - - - 18 25 - - - - - 52 15 - - - - - 55 19 | |
| R9 | - - - - - 17 10 - - - - - 17 18 - - - - - 22 22 - - - - - 22 17 | |
| R8 |
| - 8 13 - - 15 50 - 11 12 - - - 13 - 15 - - - 21 21 - 11 17 - - 21 15 |
| R7 | 8 7 13 - 17 11 40 8 17 9 - - 17 45 9 10 9 - 22 17 70 - 17 13 - 22 17 47 | |
| R6 | 12 12 12 7 15 120 20 12 15 13 17 15 52 45 10 9 8 7,5 12 27 65 15 7 15 32 12 27 22 | |
| R5 | 13 18 11 8 10 100 10 13 8 15 14 100 20 45 13 8 7 6,5 8 25 42 12 0 7 17 8 25 21 | |
| R4 | 7,5 13 8 6 8 17 - 8 7 10 11 12 17 10 - 7 - 5,5 7 22 15 10 11 7 4 7 22 15 | |
| R3 | ||
| R3 | 4 3 5 4 7 8 6 0 7 0 4 3 6 11 4 6 5 4 6 6 3 5 2 6 3 6 6 5 | |
| R2 | Ом | 2 1,5 7 2 7 8 8 3 8 7 3 15 5 13 3 5 5 4 5 4 2 2 8 5 2,5 5 4 2 |
| R1 | 1,5 1,5 0 2 7 0 7 1,5 1,5 1,5 3 15 3 13 0 - 5 4 4 3 3 1 7 4 1,5 4 3 3 | |
| J2 | - - 0 0 4 0 - - - 0 5 0 0 - - - 4 2 0 10 - - - 3 8 5 0 2 | |
| J1 | A | 0 0 2 3 4 0 10 0 1 3 7 0 0 0 0 0 4 10 0 5 7 2 4 5 7 0 5 13 |
| E3 | 6 15 8 18 0 21 13 6 3 8 25 100 45 40 7 5 8 0 100 70 45 6 - 0 0 100 0 0 | |
| E2 | B | 4 18 - 0 0 20 25 4 0 - 0 17 20 15 4 8 - 0 45 0 0 4 17 - 21 0 50 45 |
| E1 | 5 17 7 3 17 15 15 7 7 7 0 18 15 20 8 7 0 3 32 0 22 2 11 7 0 32 70 22 | |
| рисунок
| 1 2 3 4 5 6 7 1 2 3 4 5 6 7 1 2 3 4 5 6 7 1 2 3 4 5 6 7 | |
| №
| 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 | |
| R11 |
| - - - - - 11 - - - - - - 40 - - - - - - 21 - - - - - - 27 - |
| R10 | - - - - - 17 40 - - - - - 20 40 - - - - - 17 25 - - - - - 22 15 | |
| R9 | - - - - - 15 25 - - - - - 17 19 - - - - - 65 20 - - - - - 100 70 | |
| R8 |
| - - 9 - - 10 16 - 21 9 - - 10 10 - 21 21 - - 41 40 - 31 13 - - 72 22 |
| R7 | 21 21 5 - 50 8 15 21 18 7 - 50 5 8 21 13 12 - 75 17 30 7 15 13 - 7 14 70 | |
| R6 | 10 10 4 17 45 6 9 10 17 5 20 83 47 30 10 11 21 17 95 15 8 11 13 12 10 8 13 14 | |
| R5 | 15 15 12 2 40 5 8 15 14 13 18 82 17 25 15 8 20 18 85 2 7 12 17 11 8 10 20 20 | |
| R4 | 6 6 11 3 25 2 7 6 15 11 14 17 13 7 6 7 15 5 75 81 5 6 5 8 7 7 17 7 | |
| R3 | ||
| R3 | 5 5 4 4 12 8.5 2 5 1 4 5 12 6 7 5 4.5 1 7 15 5 4 5 4 5 2 1 15 10 | |
| R2 | Ом | 2 2 8 5 15 7,5 2 2 2 8 3 12 6 7 2 3 3 1 15 3 4 3 7 0 2 2 3 10 |
| R1 | 3 3 7 7 10 7 2 3 1 7 3 12 5 7 3 4 2 0,5 15 3 4 4 7 7 2 2 3 10 | |
| J2 | - - 0 0 0 0 - - - 7 8 0 - - - 7 4 30 7 - - - 0 0 0 2 - | |
| J1 | A | 0 3 3 0 0 0 0 3 0 0 0 50 7 5 3 5 3 2 20 0 10 2 3 2 0 2 15 15 |
| E3 | 6 8 15 13 170 110 75 2 3 15 15 170 110 80 6 7 15 0 200 110 80 0 0 7 15 15 110 0 | |
| E2 | B | 7 7 - 15 150 220 70 7 15 - 0 0 0 70 0 0 - 0 0 220 0 3 16 - 5 0 0 70 |
| E1 | 5 0 20 20 100 115 72 0 1 20 17 100 115 0 5 4 0 30 0 0 80 7 15 7 3 3 0 80 | |
| рисунок
| 1 2 3 4 5 6 7 1 2 3 4 5 6 7 1 2 3 4 5 6 7 1 2 3 4 5 6 7 | |
| №
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 | |
Задание для расчета (1 вариант)
Величины сопротив., ЭДС, и токов источника для каждого варианта в табл.1.1.
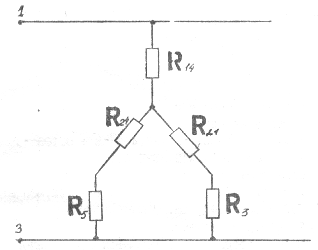
Рис.1.6.
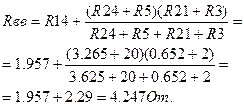
Определяем ток I6 в соответствии с (9):
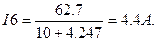
6). Составим энергетический баланс для схемы рис.1.2.
Уравнение энергетического баланса записывается в виде
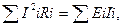
где i – 1, 2, 3……….n, - номер ветвей.
При наличии в схеме источника токов уравнение энергетического баланса примет вид:
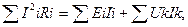
где Uk – напряжение между узлами, к которым подключен источник тока;
Ik – ток источника тока.
Для рассматриваемой схемы уравнение (1.14) в развернутом виде запишется в виде:
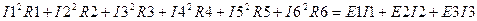 Подставляя рассчитанные значения токов, например, по методу контурных токов и значения сопротивлений, имеем:
Подставляя рассчитанные значения токов, например, по методу контурных токов и значения сопротивлений, имеем:
левая часть уравнения (1,16)
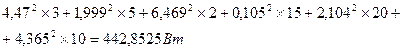
Правая часть уравнения (1.16)
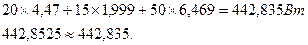
7). Построим потенциальные диаграммы для контуров Ι, ΙΙ, ΙΙΙ. По оси абсцисс откладывают сопротивления вдоль контура, по оси ординат – потенциалы.
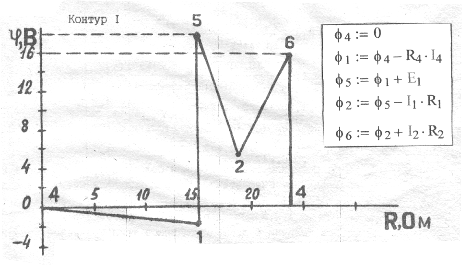
Рис. 1.7.
φ1= -1,58В; φ2= 5,01В; φ4= 0; φ5= 18,24В; φ6= 15В;
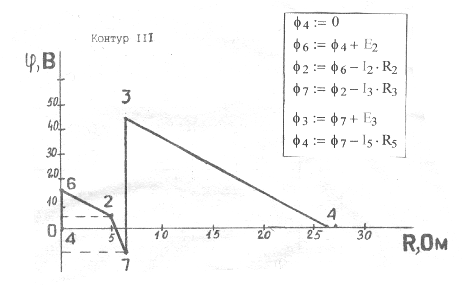
Рис.1.8.
φ7= -7,928В; φ3= 42,67В.
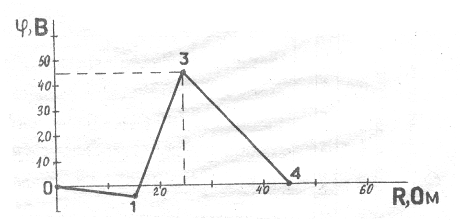
Рис. 1.9.
φ1= -1,58В; φ3= 42,67В; φ4= 0