Задание на практическую часть
Выполнить разработку цифрового фильтра с заданными характеристиками и решить следующие задачи
1) Выбрать класс фильтра;
2) Определить порядок фильтра;
3) Определить постоянную фильтра τ;
4) Провести дискретизацию передаточной функции аналогового фильтра-прототипа;
5) Определить на основании системной функции вид фильтра;
6) Определить частотный коэффициент передачи;
7) Если фильтр рекурсивный, провести проверку на его устойчивость;
8) Определить алгоритм функционирования цифрового фильтра;
9) Определить структурную схему фильтра.
Пример синтеза второго порядка
Исходные данные
Канал миографии (контроль мышечной системы легких)
1. Параметры информативного сигнала:
- амплитудное значение информативного сигнала, U k ………............…………............0,5-3 мВ
- рабочая полоса частот, DFu ……………………………......................................................1 - 20 Гц
- погрешность восстановления сигнала, DUk ……......................................…..............................3%
2. Параметры помехи:
- уровень помех, Ua………………………………............................................................0,3-0,5 мВ
- спектр помех, DFa ………………………………………….............................................10-150 Гц
2.1. Расчет параметров цифрового фильтра
1.Выбираем класс фильтра. В соответствии с рекомендациями класс фильтра выбираем в виде апериодического фильтра, описываемого уравнением (3.13).
2. Определяем порядок фильтра. Принимаем в соответствии с рекомендациями преподавателя порядок фильтра n=2.
3. Определяем постоянную фильтра τ в соответствии со следующими уравнениями, полученными путем преобразования неравенств:
1/(τ12·DFumax 2+1)n/2≤αx (2.1)
1/(τ22·(DFa max )2+1)n/2 ≥ А1,
Получаем:
[(n/2√(1/αx-1) / (DFumax) 2]1/2 ≤ τ1, (2.2)
[(n/2√(1/А1-1) / (DFa max )2]1/2 ≥ τ2,
где n - порядок фильтра; αx – отношение допустимой погрешности Δх, вносимой в полезный сигнал, к максимальному уровню помехи в сигнале; А1 - минимальное допустимое значение АЧХ фильтра при максимальной рабочей частоте DFumax; DFa max – частота помехи; τ1 – нижнее граничное значение постоянной фильтра; τ2 – верхнее граничное значение постоянной фильтра.
А1 и αx определяются следующим образом:
А1 = (U k max - D Uk доп)/U k max, (2.3)
αx = σ∆Uк /U k max, (2.4)
где U kmax – максимальное значение сигнала; D Uk доп – допустимая погрешность сигнала; σ∆Uк – случайная составляющая сигнала (см.лаб.раб.№1 стр.30).
∆ U kдоп = 0,3 мВ,
σ ∆ Uk доп = 0,1 мВ;
Подставив в выражения (2.2) и (2.3) исходные данные, получаем:
А1 = (3 мВ – 0,3 мВ)/3 мВ = 0.9;
αx = 0.1 мВ /3 мВ = 0.033.
Определим постоянную фильтра τ, подставив полученные значения А1 и αx в выражение (2.2)
[(1/0.033 -1)/(150 Гц)2]1/2 ≤ τ1,
[(1/0.9-1)/(10 Гц )2]1/2 ≥ τ2,
0.033≤ τ1 τ2 ≤ 0.036.
Таким образом, имеем следующий диапазон допустимых значений постоянной фильтра τ:
0.033≤ τ ≤ 0.036.
Выбираем постоянную фильтра τ = 0.035.
4. Проводим дискретизацию передаточной функции Wф(S)=1/(τ · s+1)2 путем перехода от передаточной функции к системной, сделав следующую замену:
s = (1-z-1)/Δ, (2.5)
где Δ = 0.00606 с (см.лаб.раб.№1 стр.32)
После преобразований получаем системную функцию:
H ( z )=1/[(0.035·(1 - z -1)/0.00606)+1]2 =(0.00606)2/(0.041 - 0.035·z -1)2=
= 0.022/(0.00169-0.00287·z -1+0.00123·z -2),
H ( z ) = 0.0023/(1-1.7·z -1+0.73·z -2). (2.6)
5. Определяем на основании системной функции H ( z ) вид фильтра
Вследствие того, что полученная системная функция (2.6) имеет следующий вид:
m n
H(z)=(∑ ak·z - k)/(1-∑ bk·z - k),
k =0 k =0
где m=0, n=2, a0=0.022, b1=1,7, b2=0.73, делаем вывод, что цифровой фильтр является рекурсивным.
6. Определяем частотный коэффициент передачи по следующей формуле:
m n
k(jwΔ)=( ∑ ak·e - jwkΔ)/(1-∑ bk· e - jwkΔ).
k=0 k=0
Получаем:
k(jwΔ) = 0.022/(1-1.7· e - jwΔ + 0.73· e -2 jwΔ).
7. Проводим проверку фильтра на устойчивость. Для этого приведем уравнение (2.6) к виду:
H(z)=А·[(z-1-β1)· (z-1-β2)…(z-1-βm)]/[(1-γ1·z-1)·(1-γ2·z-1)...(1-γ n·z-1)].
Получаем:
H(z) = 0.022/(1-0,82·z -1)·(1+0,486·z -1).
Проведем проверку фильтра на устойчивость, исходя из следующего условия: рекурсивный цифровой фильтр называют устойчивым, когда модули полюсов (корней характеристического уравнения) его системной функции меньше 1.
Поскольку γ1=0.82<1 и γ2=0.486<1, рекурсивный фильтр устойчив.
8. Определяем алгоритм функционирования фильтра. Для этого подставим в выражение (1.8) коэффициенты и получим разностное уравнение, определяющее алгоритм функционирования рекурсивного фильтра:
y(iΔ)= 0.022·x(iΔ)+ 1.7·у(iΔ-Δ)+ 0.73·у(iΔ-2Δ).
9. Ввиду того, что мы получили фильтр с системной функцией вида:
H ( z ) = 0.022/(1-1.7·z -1+0.73·z -2),
структурная схема полученного цифрового рекурсивного фильтра принимает следующий вид (рис.1)
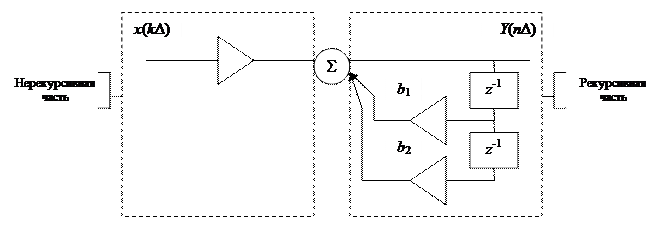
Рис.1. Структурная схема цифрового рекурсивного фильтра 2 порядка
Значения коэффициентов: а0 = 0.022; b1=1.7; b2=0.73.
Выводы
1. В ходе разработки цифрового фильтра были получены:
- тип цифрового фильтра: рекурсивный фильтр второго порядка (устойчивый);
- параметры цифрового фильтра: постоянная времени τ=0.035 и интервал дискретизации Δ=0.00606 с.
2. В ходе расчетов были получены:
- системная функция:
H ( z ) = 0.022/(1-1.7·z -1+0.73·z -2);
- частотный коэффициент передачи:
k(jwΔ) = 0.022/(1-1.7· e - jwΔ + 0.73· e -2 jwΔ);
- разностное уравнение фильтра:
y(iΔ)= 0.045·x(iΔ)+ 1.5875·у(iΔ-Δ)+ 0.625·у(iΔ-2Δ).
Из выражения (2.6) видно, что фильтр является нерекурсивным в том случае, если знаменатель этого выражения равен 1. А это возможно только при равнении нулю всех корней характеристического уравнения знаменателя (полюсов). Определяя их значения (два корня, т.к. фильтр второго порядка), получили γ1=0.82 и γ2=0.486, соответственно фильтр рекурсивный. Причем модули обоих корней – меньше единицы, что свидетельствует об устойчивости фильтра.
Литература
1. Расчет и проектирование измерительно-вычислительных систем медицинского назначения: Учебное пособие / А.А.Порунов, В.М.Солдаткин Казань: Изд-во Казан. гос. техн. ун-та, 1997. 128с.








