3. Рассчитываем проводимости ветвей схемы
.
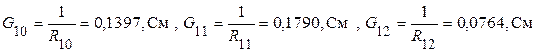4. Используя основную формулу метода, определяем узловое напряжение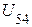 
.
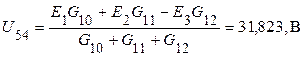Знак слагаемых числителя определяется несовпадением (+) или совпадением
(–) положительного направления 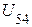и положительного направления ЭДС рассматриваемой ветви.
5. Рассчитываем неизвестные токи в ветвях, используя обобщенный закон Ома
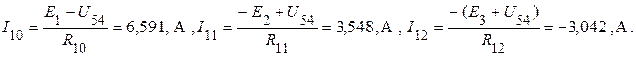
Проанализируем результаты расчета. На рис. 5 в каждой ветви источник ЭДС и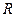 
-элементы соединены последовательно. Поэтому токи в этих ветвях равны рассчитанным. Однако участки схемы в окрестности источников не были охвачены преобразованием. Следовательно, в соответствии с условием эквивалентности преобразования участков схем величина этих токов должна остаться такой же, как и до преобразования. Сравниваем по модулю значения токов, рассчитанных настоящим методом и методом контурных токов
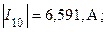
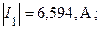
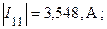
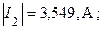
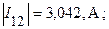
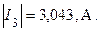
Видно, что значения токов практически совпадают. Следовательно, оба расчета проведены корректно. Третий пункт задания выполнен.
IV. Выполнение четвертого пункта задания [].
1. Разрываем шестую ветвь и произвольно задаем положительное направление токов в остальных ветвях, положительное направление напряжения холостого хода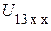 
и напряжения 
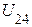между узлами 
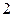и 
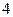(рис. 7).
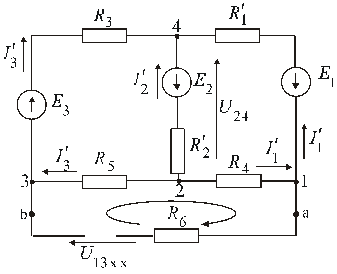
Рис.7.
2. Определяем величину 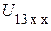. Для этого предварительно рассчитываем 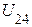методом двух узлов.
.
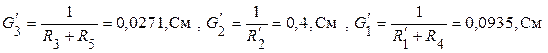Используя основную формулу метода, определяем узловое напряжение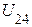
.
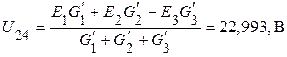Рассчитываем ток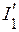и 
и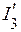 
, используя обобщенный закон Ома
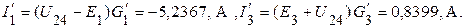
Для контура, включающего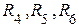 
, составляем уравнение по второму закону Кирхгофа (направление обхода контура указано круглой стрелкой) и рассчитываем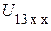
,
.
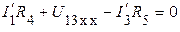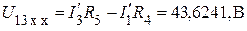3. Определяем входное сопротивление схемы со стороны зажимов разомкнутой ветви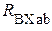 
. Для этого эквивалентно преобразуем участок схемы 
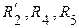, соединенный звездой, в участок, соединенный треугольником 
.
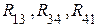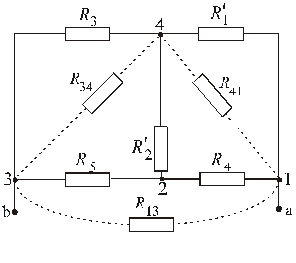
Рис. 8.
Преобразованная схема будет иметь вид (рис. 9)
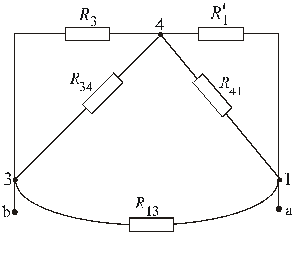
Рис. 9
.
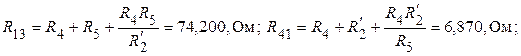
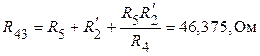Используя свойства параллельного последовательного соединения 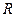- элементов, определяем
;
.
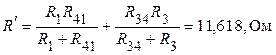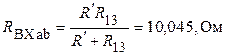4. Определяем искомый ток, используя закон Ома для замкнутой цепи
.
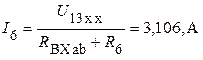Аналогичный ток, рассчитанный методом контурных токов, составляет
.
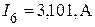Они практически совпадают. Расчет проведен верно. Четвертый пункт задания выполнен.
V. Выполнение пятого пункта задания
Составим уравнение баланса мощностей для преобразованной схемы (рис. 2) с учетом выбранного на ней положительного направления токов
1. Определяем режим работы каждого активного элемента, руководствуясь правилом. Если истинное положительное направление тока, протекающего через источник ЭДС (которое можно определить только в результате расчета), совпадает с положительным направлением ЭДС этого источника, то активный элемент работает в режиме генератора. В противном случае он работает в режиме приемника.
Сопоставляя на рис. 2 заданное положительное направление токов, знаки рассчитанных токов и положительное направление ЭДС активных элементов, определяем их режим работы
Источник ЭДС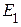 
- генератор, 
;
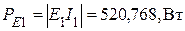источник ЭДС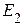 
- приемник, 
;
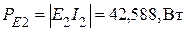источник ЭДС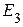 
- генератор, 
.
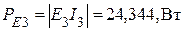2. Составляем и численно проверяем корректность уравнения баланса мощностей (значения токов берем посчитанными методом контурных токов; мощность на пассивных приемниках определяем по закону Джоуля-Ленца)
,
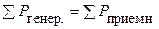где
.
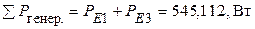
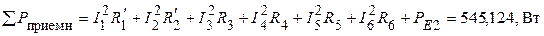Видно, что значения суммарных мощностей практически совпадают. В то же время на примере баланса мощностей покажем проверку корректности расчета любого параметра, указанного в задании. Воспользуемся абсолютным значением относительной погрешности
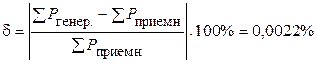
Расчет считается корректным, если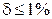 
. Итак пятый пункт задания и все задание выполнены.
Задание №2
Расчет цепи синусоидального тока
Задана эквивалентная схема цепи синусоидального тока (рис. 1) и ее параметры.
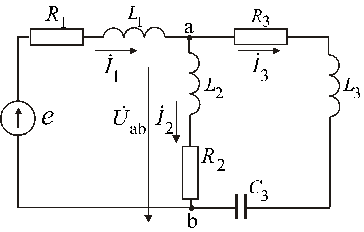
Рис. 1
.
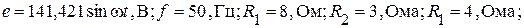
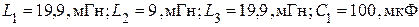Выполнить следующие действия:
1. Рассчитать токи в ветвях и напряжения на элементах схемы;
2. Составить и проверить баланс полных, активных и реактивных мощностей;
3. Построить векторную диаграмму токов для узла а.
Расчет проводим символическим методом в следующем порядке:
1. Рассчитываем сопротивление всех элементов схемы (учитываем, что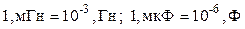 
)
.
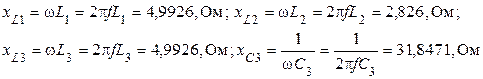2. Представляем ЭДС источника в виде комплекса действующего значения. Определяем комплексные сопротивления и проводимости ветвей
.
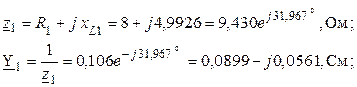
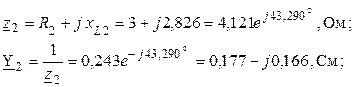
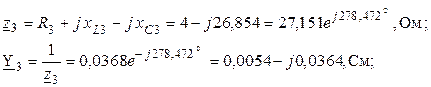
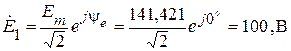3. Рассчитываем токи в ветвях методом двух узлов. Задаем произвольно положительное направление токов в ветвях и положительное направление узлового напряжения. Используя основную формулу метода, рассчитываем узловое напряжение
.
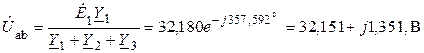Определяем токи в ветвях, используя обобщенный закон Ома
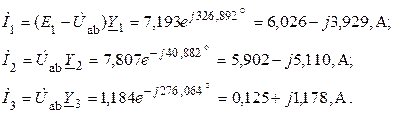
Проверяем корректность промежуточных расчетов, составив уравнение по первому закону Кирхгофа для узла а
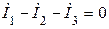
Комплексная абсолютная погрешность расчета составляет
.
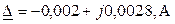Определяем ее модуль
.
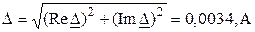Рассчитываем относительную погрешность определения токов
.
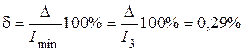Поскольку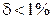 
, расчет токов корректен. Первый пункт задания выполнен.
4. Составляем и проверяем баланс мощностей
Рассчитываем полную комплексную мощность, развиваемую источником, а также его активную и реактивную мощность. При этом используем закон Джоуля-Ленца в комплексной форме записи
,
.
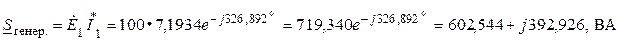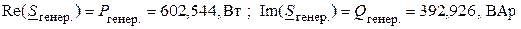Определяем суммарную активную и реактивную мощность на приемниках. При этом также используем закон Джоуля-Ленца
;
.
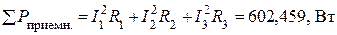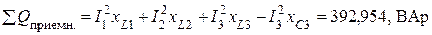Рассчитываем суммарную полную комплексную мощность на приемниках
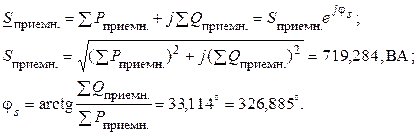
Проверяем корректность расчета, рассчитав модуль относительной погрешности определения полных мощностей
.
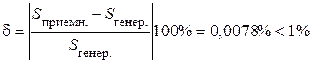Расчет проведен корректно. Второй пункт задания выполнен.
4. Строим векторную диаграмму токов на комплексной плоскости, используя их действительные (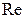 
) и мнимые ( 
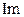) составляющие. Задаемся масштабом по току 
,
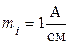делим указанные составляющие токов на масштаб и откладываем получающиеся отрезки в сантиметрах вдоль осей комплексной плоскости (с учетом знаков составляющих)
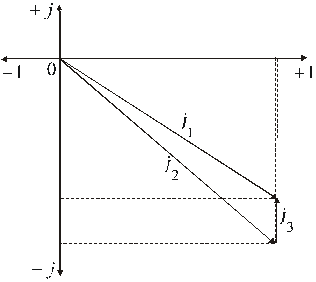
Рис. 2.
Результаты построения (рис. 2) наглядно иллюстрируют корректность проведенных расчетов. Итак, третий пункт и все задание выполнены.
Задание №3
Расчет трехфазной цепи
Заданы эквивалентная схема замещения трехфазного приемника и ее параметры, а также задано линейное напряжение со стороны приемника
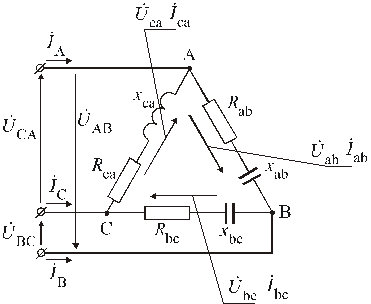
Рис. 1.
.
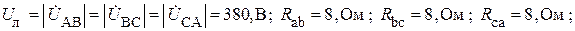
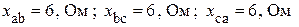Выполнить следующие действия:
1. Определить линейные токи, фазные токи и фазные напряжения;
2. Рассчитать активную, реактивную мощность на всем приемнике и на каждой фазе в отдельности;
3. Построить на комплексной плоскости векторную диаграмму токов и напряжений.
Расчет проводим в следующем порядке:
1. Определяем комплексы действующих значений фазных ЭДС
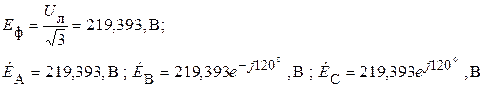
2. Определяем комплексы действующих значений линейных и фазных напряжений
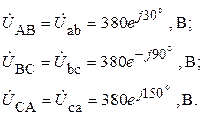
3. Рассчитываем комплексные сопротивления фаз приемника
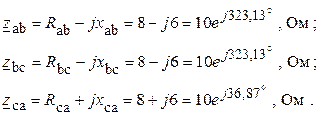
4. По закону Ома определяем фазные токи
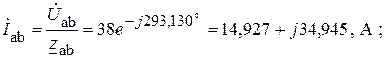
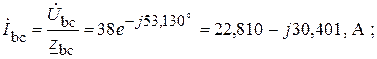
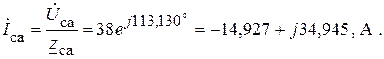
5. Рассчитываем линейные токи, используя первый закон Кирхгофа
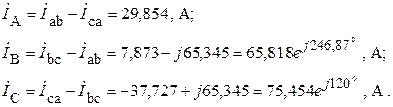
6. Определяем полные комплексные, полные, активные и реактивные мощности каждой фазы и эти же мощности на всем трехфазном приемнике
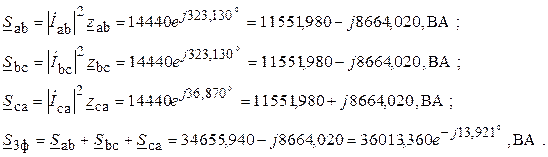
При этом
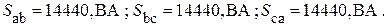
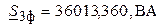
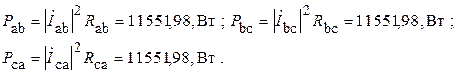
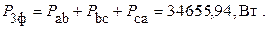
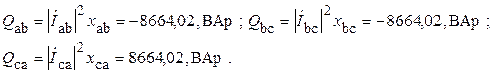
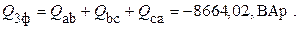
Без специальной проверки видно, что баланс мощностей подтверждается. Следовательно расчеты проведены корректно.
7. Строим векторную диаграмму токов, напряжений и ЭДС. Задаемся масштабами по току и по напряжению
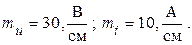
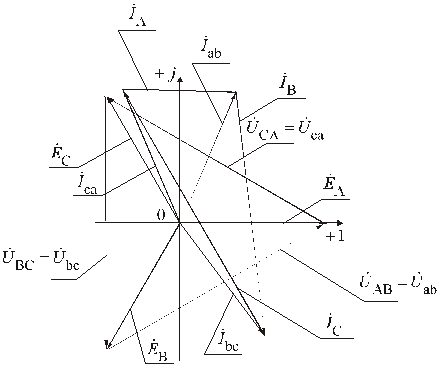
Рис. 2.
Третий пункт и все задание выполнено.
Рекомендуемая литература
Основная
1. Касаткин А.С., Немцов М.В. Электротехника. – М.: Издательский центр «Академия», 2003.