5. Полученную систему упорядочиваем
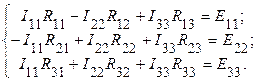
и представляем в матричной форме записи, подставив численные значения составляющих системы контурных уравнений
.
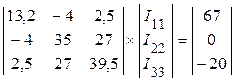6. Решаем полученную систему контурных уравнений, используя правило Крамера []:
6.1. Вычисляем главный определитель системы, разворачивая квадратную матрицу контурных сопротивлений по первой строке (следует заметить, что величина определителя не зависит от того, по какой строке или столбцу его разворачивают)
;
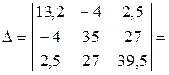
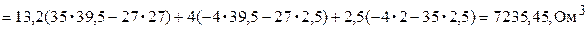6.2. Вычисляем дополнительные определители системы, последовательно заменяя столбцы матрицы контурных сопротивлений матрицей-столбцом контурных ЭДС. Каждый дополнительный определитель рассчитываем, разворачивая его по первой строке аналогичным образом
;
;
;
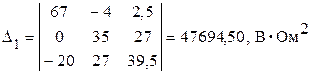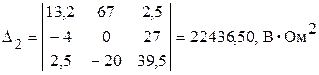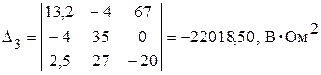6.3. Определяем контурные токи
; 
; 
.
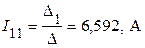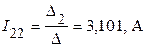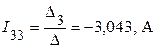7. Используя рассчитанные контурные токи, определяем реальные токи в ветвях схемы. Руководствуемся правилом: реальные токи в независимых ветвях схемы (принадлежащих только одному контуру) определяются только контурным током рассматриваемого контура
.
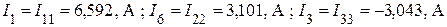Реальные токи в общих ветвях между смежными контурами определяются по принципу наложения: алгебраической суммой смежных контурных токов. При этом знак каждого контурного тока определяется совпадением (+) или несовпадением (–) его направления с заданным положительным направлением реального тока в рассматриваемой ветви.
.
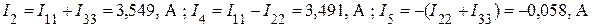Второй пункт задания выполнен.
III. Выполнение третьего пункта задания.
Рассматриваемая схема замещения содержит четыре узла, поэтому к заданной схеме метод двух узлов непосредственно не применим.
1. Используя эквивалентное преобразование участка схемы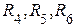 
, соединенного по схеме «треугольник», в участок 
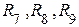, соединенный по схеме «звезда» (отмечен на рис. 4 пунктиром), приводим начальную схему к схеме, содержащей два узла (рис.5).
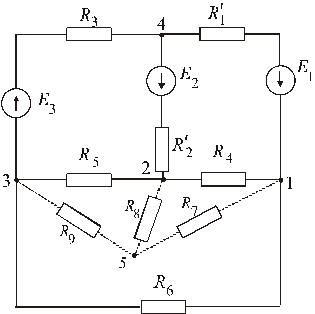
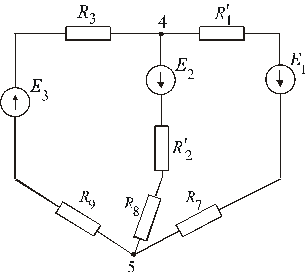
Рис. 4 Рис. 5
При этом
.
.
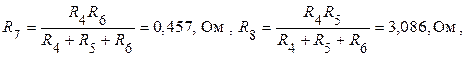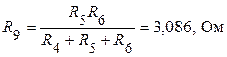Эквивалентно объединяя последовательно соединенные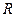 
-элементы в каждой ветви, получаем исходную схему для расчета методом двух узлов (рис. 6).
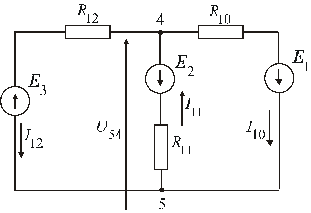
Рис. 6
При этом
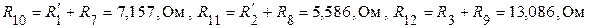
2. Произвольно задаем положительное направление токов в ветвях схемы и положительное направление узлового напряжения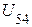 
(рис. 6)