Определение скорости звука в воздухе
И ПОКАЗАТЕЛЯ АДИАБАТЫ ВОЗДУХА МЕТОДОМ
СТОЯЧЕЙ ВОЛНЫ
Цель работы: исследование упругих и тепловых свойств воздуха.
Оборудование: труба с подвижной стенкой на одном из концов, звуковой генератор, электронный осциллограф, термометр.
Введение
Скорость распространения звуковых волн в среде определяется, в первую очередь, упругими свойствами этой среды. Газы обладают только объемной упругостью. Поэтому в них могут распространяться только продольные волны, в которых чередуются области сгущения и разрежения газа. Скорость звука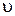 
в общем случае определяется выражением
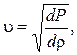(1)
где P – давление в газе;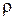 
– плотность газа.
Лаплас установил, что в звуковой волне в газе колебания происходят настолько быстро, что теплообмен между областями разрежения и сгущения не имеет места. Распространение звука в газе – адиабатический процесс. Уравнение Пуассона для адиабатического процесса:
РV γ = const, (2)
где γ = Cp / Cν – показатель адиабаты; Cp – теплоемкость при постоянном давлении; Cv – теплоемкость при постоянном объеме; V – объем. Если учесть, что плотность 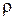пропорциональна 1/ V, то для дифференциала левой части (2) получается
γРdρ – ρdР = 0. (3)
Отсюда скорость звука в газе
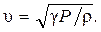(4)
Из уравнения состояния идеального газа в форме
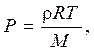(5)
(где M – молярная масса газа; R – универсальная газовая постоянная, Т – абсолютная температура) и соотношения (4) следует формула для показателя адиабаты
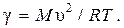(6)
Формула (6) используется в данной лабораторной работе для определения показателя адиабаты воздуха.
Скорость звука определяется методом стоячей волны. Стоячая волна образуется, например, при положении двух плоских гармонических волн, бегущих в противоположных направлениях по оси X:
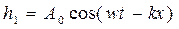и 
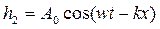, (7)
где h1, h2 – смещение частиц среды в первой волне и во второй волне соответственно; A0 – амплитуда колебаний;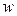 
– циклическая частота; k – волновое число. Результирующая волна имеет вид
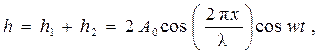(8)
где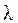 
– длина звуковой волны.
Это стоячая волна, которая характеризуется, как следует из формулы (8), чередующимися пучностями и узлами. В местах расположения пучностей амплитуда стоячей волны максимальна, в местах расположения узлов амплитуда стоячей волны равна нулю. Расстояние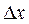 
между соседними узлами и между соседними пучностями одинаково и равно
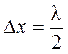. (9)