Лабораторная работа № 1-10
ОПРЕДЕЛЕНИЕ МОДУЛЯ ЮНГА МЕТОДОМ
РАСТЯЖЕНИЯ ПРОВОЛОЧНЫХ ОБРАЗЦОВ
Цель работы: исследование зависимости деформации металлов от приложенного напряжения в области других деформаций.
Оборудование: лабораторная установка для растяжения образцов, масштабная линейка, штангенциркуль или микрометр, технические весы и разновесы.
Введение
Под действием приложенных сил тела деформируются, т.е. изменяют свою форму или объем. Деформации делятся, главным образом, на упругие и пластические. Упругими называются такие деформации, которые исчезают полностью после прекращения действия на твердое тело сил. Если тело остается деформированным и при отсутствии сил, то такие деформации называются пластическими, или остаточными. Степень деформации характеризуется величиной ε - относительной деформацией. Для однородного стержня, прямолинейного отрезка проволоки и т.д. относительную деформацию можно определить как отношение удлинения стержня D l к величине первоначальной длины l0 : ε = D l / l0. В этом случае напряжение определяется как отношение величины растягивающей силы Fn, приложенной перпендикулярно к поперечному сечению стержня, к площади поперечного сечения стержня Sn : s = Fn / Sn. При упругих деформациях существует однозначная зависимость между напряжением и относительной деформацией. При пластических деформациях такая однозначная связь отсутствует.
При малых упругих деформациях, которые встречаются наиболее часто, связь между напряжением и деформацией описывается законом Гука
s = E ε, (1)
где E - модуль Юнга, важнейшая постоянная, характеризующая упругие свойства вещества. Модуль Юнга зависит от типа твердого тела и его физического состояния (например температуры). В данной лабораторной работе и определяется модуль Юнга различных металлов.
Описание установки
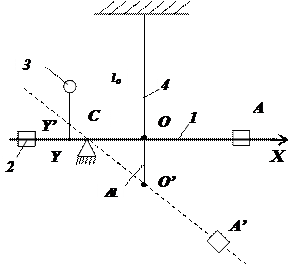
Для определения модуля Юнга используется установка, схема которой представлена на рисунке. Установка состоит из рычага 1, закрепленного в шарнире в точке С, неподвижного груза 2, регулирующего первоначальную нагрузку, подвижного груза А, задающего величину напряжения в данной установке, и измерительного инструмента 3, в точке Y соприкасающегося с рычагом. Проволочный образец 4 одним концом жестко закрепляется в неподвижной стойке (на рисунке не показано), а другим, к которому прикладывается растягивающая сила, в точке O прикрепляется к рычагу 1. На рисунке сплошным отрезком YA показано положение рычага, когда образец не растянут и показание индикатора N (в миллиметрах) равно нулю. Пунктирным отрезком Y’ A’ показано положение рычага, когда из-за смещения A напряжение отлично от нуля и образец 4 растягивается на величину D l. Из подобия треугольников COO’ и CYY’ следует
.
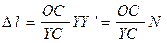Отсюда для относительной деформации имеем
.
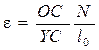Величина растягивающей силы Fn определяется разностью приложенных сил к проволочному образцу в точке O для двух положений подвижного груза A и A’ , т.е. Fn = F’ – F.
По правилу рычага в равновесии имеем
; 
,
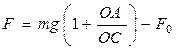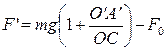где m - масса подвижного груза A, F0 - добавка, обусловленная влиянием неподвижного груза 2. Окончательно для силы растягивания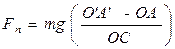 
, а для напряжения
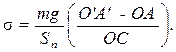
Из приведенной формулы следует, что на данной установке возможно изменение величины s простым способом: изменением величины разности O ’ A ’ – OA , что и используется в лабораторной работе. Для удобства расчетов вводится ось OX вдоль рычага, как показано на рисунке. Тогда, обозначив OA через X0, а O ' A ' через X , получим:
, 
.
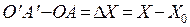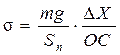Порядок выполнения работы
1. Настроить установку. Для этого груз A располагают так, чтобы OA (X0) равнялось 5 – 6 см. Конец O проволочного металлического образца вставляют в пазы рычага и стойки. Устанавливая груз 2, добиваются того, чтобы показание индикатора 3 равнялось нулю.
2. Измерить параметры установки: величины отрезков OC , YC и массу груза A.
3. Измерить параметры образца: l0 (первоначальная длина) и d (диаметр).
4. Изучить зависимость ε от s. Для этого перемещать груз A от начального положения X0 до конца рычага 1 (нагрузка) и обратно (разгрузка) к первоначальному положению ступенчато через 2 см, занося результаты измерений в таблицу. В таблицу также рекомендуется заносить и результаты расчетов D l , Fn, ε, s .
| № п/п | Положение груза D X, см | Показание индикатора N, деления | Удлинение D l , м | Растягивающая сила Fn, Н | ε = D l / l 0 | s = Fn / Sn , , Н/м2 |
| 1 2 . . |
5. Построить график зависимости ε от s. Проанализировать полученную зависимость.
6. Выделить на графике прямолинейный участок, и для экспериментальных точек, составляющих этот участок, методом наименьших квадратов (см. “Элементарная обработка результатов физического эксперимента”) найти модуль Юнга металлического образца.
7. Вставить новый проволочный образец из другого металла. Выполнить пп. 3 – 6.
8. Сравнить и проанализировать полученные значения модуля Юнга, ход зависимости ε от s для разных металлов.
Контрольные вопросы
1. Чем характеризуется область деформаций, соответствующих закону Гука?
2. Почему начальное положение X0 груза A выбирается отличным от нуля?
3. Почему на графике зависимости ε ( s ) часть экспериментальных точек не ложится на прямолинейный участок?
4. От чего зависит величина модуля Юнга твердого тела?
Список рекомендуемой литературы
1. Сивухин Д.В. Общий курс физики: В 5 т. Т. 1. Механика. М.: Наука, 1979. § 73. – 519 с.
2. Стрелков С.П. Механика. – М.: Наука, 1965. § 81. – 560 с.
3. Методические указания к лабораторным работам по физике. Механика / Под ред. Н.Г. Конопасова. Владим. политехн. ин-т. – Владимир, 1983. – 45 с.
2. Молекулярная физика
в лабораторных работах данного раздела физики учащиеся знакомятся с особенностями процессов, протекающих в молекулярных системах, и осваивают методы определения важнейших параметров, характеризующих жидкое и газообразное состояния вещества. Студентам рекомендуется четко разделять при действии установок стационарные процессы, неравновесные процессы и равновесные состояния.
Лабораторная работа № 2-2