2. Сквайрс Дж. Практическая физика. – М.: Мир, 1971. – 248 с.
Министерство образования Российской Федерации
Владимирский государственный университет
Кафедра общей и прикладной физики
ФИЗИКА
Методические указания к комплексу лабораторных работ
по физике для студентов-заочников (механика, молекулярная физика, электричество и магнетизм, колебания и волны,
оптика)
Под редакцией А.А. Кулиша
Владимир 2004
УДК 53 (07)
Составители:
А.Ф. Галкин, Е.В. Дмитриева, А.А. Кулиш, В.С. Плешивцев
Рецензент
Кандидат физико-математических наук, доцент
Владимирского государственного педагогического университета
А.В. Гончаров
Печатается по решению редакционно-издательского совета
Владимирского государственного университета
Физика. Методические указания к комплексу лабораторных работ по физике для студентов-заочников (механика, молекулярная физика, электричество и магнетизм, колебания и волны, оптика) / Владим. гос. ун-т; Сост.: А.Ф. Галкин и др.; Под ред. А.А. Кулиша. Владимир 2004. 108 c.
Комплекс лабораторных работ по физике соответствует требованиям государственных стандартов инженерно-технических специальностей вузов. Методические указания состоят из вводной части, введения к каждому разделу и описания 21 лабораторной работы. В данном издании выделены основные части полного лабораторного практикума и важнейшие типы лабораторных работ по механике, молекулярной физике, электромагнетизму, колебаниям и волнам, оптике.
Методические указания направлены на организацию самостоятельной работы студентов заочной формы обучения при подготовке и выполнении лабораторных работ.
Предназначены для студентов заочной формы обучения. Могут быть использованы студентами дневной и вечерней форм обучения.
Вводная часть, разд. «Механика» и «Молекулярная физика» подготовлены доцентом А.А. Кулишом, разд. «Электричество и магнетизм», «Колебания и волны» – доцентом В.С. Плешивцевым и ассистентом Е.В. Дмитриевой, разд. «Оптика» – доцентом А.Ф. Галкиным.
Табл. 11. Ил. 56. Библиогр.: 26 назв.
| |
УДК 53 (07)
ПРЕДИСЛОВИЕ
В основе заочной формы обучения лежит самостоятельная работа студентов. Изучение физики самостоятельно – кропотливый, многогранный труд. Учебная работа по физике – комплексная: это изучение теории, решение задач и, что особенно важно, практическая проверка законов при выполнении лабораторных работ. По заочной форме обучения учебных аудиторных часов немного, поэтому с целью оптимизации учебного процесса в данном издании выделены основные части лабораторного практикума и важнейшие типы лабораторных работ. Выполнение представленных лабораторных работ позволяет, в целом, достаточно широко охватить физический практикум по механике, молекулярной физике, электромагнетизму, колебаниям и волнам, оптике и составить целостное представление о методах физического исследования и практического проявления законов физики.
Описание лабораторных работ основано на методических материалах для очной формы изучения физики с достаточно большим числом аудиторных часов. Поэтому мы позволили себе оставить соответствующую нумерацию лабораторных работ. Студенты-заочники при необходимости могут обращаться к описанию полного лабораторного практикума, в составлении которого также принимали участие преподаватели кафедры общей и прикладной физики: М.И. Андреева, О.Я. Бутковский, Л.В. Грунская, В.В. Дорожков, В.Н. Кунин, В.П. Кондаков, А.А. Шишелов.
Нами оставлены также дополнительные задания, позволяющие студентам заочной формы обучения выполнять лабораторные работы с элементами научного исследования и использовать компьютеры.
ВВЕДЕНИЕ
Физика – наука опытная: главная роль в установлении физических закономерностей принадлежит эксперименту. Эксперимент – система логически связанных целенаправленных действий. В физике в основе опытов лежат методы измерений величин и поэтому центральным является понятие методики проведения измерений.
При измерениях физических величин выполняются три последовательные операции: 1) создание экспериментальных условий, 2) наблюдение, 3) отсчет.
Создание экспериментальных условий, при которых проводятся измерения (постоянная величина напряжения или давления, значительный перепад температур, малые крутильные колебания и т.д.), осуществляется с помощью приборов, специализированных установок, электрических схем и т.п.
Отсчет следует за наблюдением и производится, как правило, по шкале с некоторым масштабом. В результате появляются “первичные экспериментальные данные”. Обработка результатов эксперимента и позволяет определить измеряемую величину.
ЭЛЕМЕНТАРНАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ
ФИЗИЧЕСКОГО ЭКСПЕРИМЕНТА
Под измерением понимается сравнение измеряемой величины с другой величиной, принятой за единицу измерения.
Измерения делятся на прямые и косвенные.
При прямых измерениях определяемая величина сравнивается с единицей измерения непосредственно или при помощи измерительного прибора, проградуированного в соответствующих единицах. Примеры: измерение длины линейкой, измерение масс с помощью набора разновесов на рычажных весах, измерение силы электрического тока амперметром.
При косвенных измерениях измеряемая величина вычисляется из результатов прямых измерений других величин, которые связаны с измеряемой величиной определенной функциональной зависимостью. Примеры: измерение скорости тела v с использованием формулы v = s / t , где s – пройденный телом путь за время t при равномерном прямолинейном движении; измерение скорости свободного падения g при колебаниях математического маятника по известной формуле 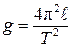 , где ℓ – длина математического маятника, Т – период колебаний математического маятника. Величины s, t, ℓ, T определяются в прямых измерениях.
, где ℓ – длина математического маятника, Т – период колебаний математического маятника. Величины s, t, ℓ, T определяются в прямых измерениях.
Физические величины являются вполне определенными, неслучайными (толщина пластины, разность температур, время между двумя событиями). Однако в процессе измерения из-за влияния различных случайных факторов (колебания почвы, перепады температуры и давления, изменение положения экспериментатора при отсчете по шкале и т.д.) результаты измерения – случайные величины. Основная задача при проведении измерений – указать наиболее точное значение измеряемой величины и ошибку (погрешность) измерения. Например, при измерении фокусного расстояния линзы f получено: f = (81 + 1) мм. Это означает, что наиболее точное значение фокусного расстояния равно 81 мм, а ошибка определения f – 1 мм.
Величина погрешности используется при сравнительном анализе экспериментальных данных, позволяющем сделать обоснованный вывод. Например, необходимо установить, зависит ли сопротивление проволочной катушки от температуры. Измеренное сопротивление катушки оказалось равным 18,22 Ом при температуре 15°С и 18,31 Ом при 25°С. Следует ли придавать значение разнице этих величин? Если ошибка составляет 0,01 Ом, то разница значима, если ошибка равна 0,10 Ом, то – незначима. Для первого случая вывод: сопротивление катушки зависит от температуры. Во втором случае вывод: сопротивление катушки не зависит от температуры в пределах погрешности измерения.
Ошибки (погрешности) измерения делятся на два типа: систематические и случайные.
Систематическая ошибка – ошибка, которая остается постоянной на протяжении всей серии измерений. Систематические погрешности, как правило, обусловлены: 1) неисправностью измерительных приборов, 2) ошибочностью выбранного метода измерений, 3) упущениями со стороны наблюдателя. Их можно уменьшить, относясь критически к методам измерения и строго следя за исправным состоянием приборов. Если на измерительном инструменте не указана погрешность измерения, то за величину систематической ошибки принимается половина цены деления шкалы.
Случайная ошибка – ошибка, которая изменяется произвольным образом от одного измерения к другому, в равной степени может быть как положительной, так и отрицательной. Случайные ошибки оцениваются методами математической статистики. Рассмотрим некоторые положения этой теории.
Прямые измерения
Обозначим истинное значение некоторой физической величины через x. Результаты n отдельных измерений – х 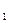 , х
, х 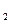 ,…, х
,…, х  (случайные величины). Тогда абсолютной ошибкой D х i i-го измерения называется разность: Dх
(случайные величины). Тогда абсолютной ошибкой D х i i-го измерения называется разность: Dх 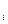 = х – х
= х – х 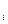 . Абсолютные ошибки также являются случайными величинами. Огромное количество опытных фактов, накопленных в экспериментальной физике, позволяет установить два основополагающих предположения относительно абсолютных ошибок измерения:
. Абсолютные ошибки также являются случайными величинами. Огромное количество опытных фактов, накопленных в экспериментальной физике, позволяет установить два основополагающих предположения относительно абсолютных ошибок измерения:
1. При большом числе измерений случайные абсолютные ошибки одинаковой величины, но разного знака встречаются одинаково часто.
2. Большие (по абсолютной величине) погрешности встречаются реже, чем малые, т.е. вероятность появления погрешности уменьшается с ростом величины погрешности.
Эти два предположения лежат в основе теории ошибок.
Найдем наиболее точную оценку величины х. С этой целью проведем ряд преобразований. Величины отдельных измерений можно выразить так:
х 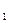 = х - Dх1;
= х - Dх1;
х 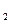 = х - Dх2;
= х - Dх2;
……………
х n = х - Dх n .
Почленное сложение всех равенств дает: 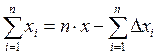 .
.
Отсюда для х получим
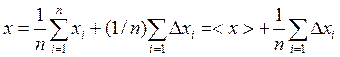 ,
,
где 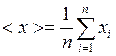 – среднее арифметическое из n измерений.
– среднее арифметическое из n измерений.
Из предположения 1 при n® ¥ следует: 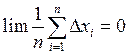 .
.
Поэтому при бесконечно большом числе измерений x = < x >. Однако в реальном эксперименте число измерений всегда ограничено, т.е. x @ < x >. При обработке результатов измерений в качестве наиболее точного значения величины х принимается среднее арифметическое из n измерений.
Для оценки отклонения истинного значения х от среднего арифметического рассмотрим некоторые понятия теории вероятности.
Случайная величина может быть дискретной (выпадение герба монеты или какой-либо грани кубика при подбрасывании), т.е. принимать ряд дискретных значений, или непрерывной (температура в помещении).
Для дискретной величины: если в N опытах случайная величина появляется N i раз, то вероятность Р появления этой величины равна
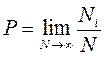 .
.
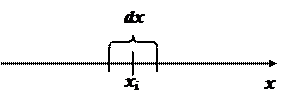 Пример. Если подбросить монету 10 раз, то пусть герб выпадет 3 раза и vi = 0,3 (vi = Ni / N – относительная частота появления герба в опыте). Но если подбросить монету 105 раз, то vi будет очень близко к 0,5. Если подбросить 1010 раз, то vi будет еще ближе к 0,5. Таким образом, величина 0,5 – вероятность появления герба в опыте. Понятие вероятности справедливо для случайных процессов. Мы не знаем, появится ли данное событие (выпадение герба) в опыте, но мы характеризуем появление этого события понятием вероятности и численным значением вероятности.
Пример. Если подбросить монету 10 раз, то пусть герб выпадет 3 раза и vi = 0,3 (vi = Ni / N – относительная частота появления герба в опыте). Но если подбросить монету 105 раз, то vi будет очень близко к 0,5. Если подбросить 1010 раз, то vi будет еще ближе к 0,5. Таким образом, величина 0,5 – вероятность появления герба в опыте. Понятие вероятности справедливо для случайных процессов. Мы не знаем, появится ли данное событие (выпадение герба) в опыте, но мы характеризуем появление этого события понятием вероятности и численным значением вероятности.
Если случайная величина х – непрерывная, то ставится вопрос: какова вероятность того, что случайная величина окажется в опыте в определенном бесконечно малом интервале dx около некоторого значения х i .
Эта вероятность пропорциональна ширине интервала dx и зависит от значения xi , т.е. dP ( x ) = y ( x ) dx . За вероятность появления случайной величины х в интервале dx около значения xi dP ( xi ) = y ( xi ) dx принимают относительную частоту появлений этой величины в интервале dx около значения xi, когда число измерений стремится к бесконечности.
Главную роль в описании случайной величины, распределенной непрерывно, играет функция y ( x ), которая называется функцией распределения вероятностей.
В математической статистике показано, что при выполнении предположений 1 и 2 функция распределения имеет вид (на рис.1 представлен график этой функции): 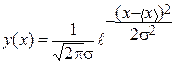 , где s2 – дисперсия распределения.
, где s2 – дисперсия распределения.
Распределение случайной величины такого типа называется нормальным распределением, или распределением Гаусса.
Как видно из рис. 1, дисперсия показывает, насколько широко разбросаны значения случайной величины относительно среднего значения.
Из теории математической статистики следует, что при n измерениях наиболее точную оценку дисперсии дает выражение
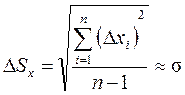 .
.
Величина DSx называется среднеквадратичной погрешностью отдельного измерения.
Среднеквадратичная погрешность отдельного измерения характеризует разброс результатов единичных измерений около среднего значения. Но главная цель – оценить, насколько среднее значение близко к истинному. Если для этого рассмотреть серии измерений из n1 опытов, n2 и т.д., то в каждой серии можно определить < x1>, < x2>, < x3> и т.д. Эти средние значения будут отличаться друг от друга, и, более того, совокупность этих средних значений представляет собой набор случайных величин. Эти случайные величины также распределены по нормальному закону, который и будет характеризовать отличие < x > от истинного, но с другой дисперсией <s2>. В теории математической статистики показано, что наилучшей оценкой <s> распределения средних значений является величина
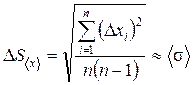 .
.
Величина 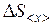 называется среднеквадратичной погрешностью среднего. Величины s и <s> связаны соотношением
называется среднеквадратичной погрешностью среднего. Величины s и <s> связаны соотношением 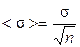 , причем s – величина постоянная, так как характеризует разброс результатов отдельных измерений. Поэтому, чем больше число измерений, тем меньше среднеквадратичная погрешность среднего <s> и тем меньше различие между <х> и истинным значением х. При выполнении лабораторных работ число измерений обычно равно 5 ¸ 10.
, причем s – величина постоянная, так как характеризует разброс результатов отдельных измерений. Поэтому, чем больше число измерений, тем меньше среднеквадратичная погрешность среднего <s> и тем меньше различие между <х> и истинным значением х. При выполнении лабораторных работ число измерений обычно равно 5 ¸ 10.
Характеристикой того, как сильно среднее арифметическое значение отличается от истинного, служит доверительный интервал, для которого известно, с какой вероятностью истинное значение может находиться внутри этого интервала. Величина этой вероятности выбирается экспериментатором и называется надежностью. При выполнении лабораторных работ рекомендуется надежность a, равная 0,95. Величина доверительного интервала Dх с заданной надежностью a равна
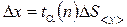 ,
,
где ta( n ) – коэффициент Стьюдента, который можно найти в таблице для n измерений и надежности a. Окончательный результат записывается в форме х = <х> + Dх с надежностью a. При заметной величине систематической погрешности ошибки объединяют по формуле
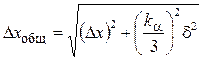 ,
,
где 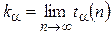 ; d – систематическая погрешность прибора.
; d – систематическая погрешность прибора.
Часто для оценки погрешности используют относительную ошибку Е, которая определяется выражением 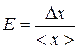 или в процентах:
или в процентах: 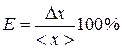 .
.
Косвенные измерения
В математической статистике показано, что результат косвенных измерений < z > и погрешность косвенных измерений Dz (доверительный интервал), если зависимость имеет вид z = f ( x , y ,…), определяются выражениями
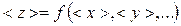 ,
,
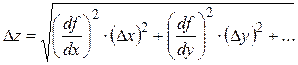 ,
,
где <х>, <у>, … – результат прямых измерений; Dx, Dy, … – доверительные интервалы величин x, y, …, полученных в прямых измерениях. Результаты косвенных измерений записываются окончательно в виде z = < z > ± Dz, 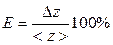 .
.
Ниже в табл. 1 представлены выражения < z > и Dz для ряда наиболее часто встречающихся зависимостей.
Таблица 1
| Вид функции | Среднее значение | Погрешность (Dz либо Dz/z) |
| z = x ± y | <z> = <x> ± <у> |  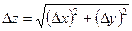
|
| z = x × y z = x/y, z = y/x | <z> = <x> × <у> <z> = <x>/<у>, <z> = <у>/<x> | 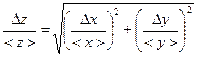
|
| z = xn | <z> = (<x>)n | 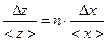
|
| z = ℓn x | <z> = ℓn <x> | 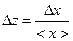
|
| z = ℓx | ázñ = ℓáxñ | 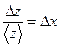
|
Представление экспериментальных результатов
Полученные в опыте значения измеряемой величины заносятся, как правило, в таблицу либо представляются в виде графика.
В табл. 2 указываются единицы измерения физических величин и десятичный множитель.
Таблица 2
| № п/п | Материал | s, Н/м2 | Dℓ/ℓ0 | Е×10-10, Н/м2 |
| 1 | Латунь | |||
| 2 | Алюминий |
 Представление результатов измерений в виде графиков необходимо для наглядности и определения ряда величин. Масштаб выбирается таким, чтобы, во-первых, экспериментальные точки не сливались, во-вторых, обозначался простыми числами (10, 100, 0,1 и т.д. единиц соответствовали 1 см), в-третьих, занимал размеры около страницы. По осям откладываются деления и указываются символы величин и их единицы измерения. Погрешности изображаются в виде отрезков длиной в доверительный интервал. На рис. 2 представлен график зависимости углового ускорения ε от момента внешних сил М маятника Обербека, полученный в лабораторной работе “Изучение динамики вращательного движения твердого тела”.
Представление результатов измерений в виде графиков необходимо для наглядности и определения ряда величин. Масштаб выбирается таким, чтобы, во-первых, экспериментальные точки не сливались, во-вторых, обозначался простыми числами (10, 100, 0,1 и т.д. единиц соответствовали 1 см), в-третьих, занимал размеры около страницы. По осям откладываются деления и указываются символы величин и их единицы измерения. Погрешности изображаются в виде отрезков длиной в доверительный интервал. На рис. 2 представлен график зависимости углового ускорения ε от момента внешних сил М маятника Обербека, полученный в лабораторной работе “Изучение динамики вращательного движения твердого тела”.
В физике широко распространена линейная зависимость между величинами, в том числе и между теми, которые изучаются экспериментально. В этом случае наилучший вид аппроксимирующей прямой может быть выбран методом наименьших квадратов. Рассмотрим этот метод.
Пусть в эксперименте в n измерениях получены пары значений ( x1, y1), ( x2, y2), … , ( xn , yn ), отвечающие зависимости y = ax + b, параметры a и b которой должны быть найдены. Предполагается, что с погрешностями определена лишь совокупность значений y. Тогда отклонение в каждом i-м изменении значения аппроксимирующей прямой от экспериментально полученного yi составляет: yi – axi – b. Наилучшие значения a и b выбираются так, чтобы сумма квадратов ошибки 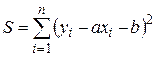 была минимальной. Из условия минимума следует
была минимальной. Из условия минимума следует
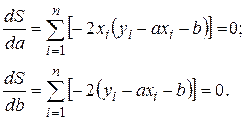
Для определения a и b получается система из двух уравнений
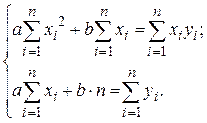
Отсюда вытекают формулы для искомых a и b
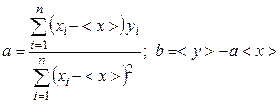 .
.
Приближенные вычисления
Результат измерений представляет собой приближенное число, точность которого определяется ошибкой.
Пусть, например, в опыте с математическим маятником погрешность определения ускорения свободного падения равна 0,05 м/с2, а g равно 9,83 м/с2. Результат записывается в виде g = 9,83 ± 0,05 м/с2. Очевидно, что вычислять результат опыта с точностью до тысячных долей не имеет смысла, так как ошибка составляет сотые доли, и тем более бесполезно указывать тысячные доли при записи результата.
Полученное число (результат измерений) – приближенное, последняя цифра – сомнительная, а остальные верные. Так получается при любых измерениях.
При записи окончательного результата оставляют только значащие цифры (верные и сомнительную цифры). Если приближенное число входит в расчетную формулу, в нем сохраняют одну “неверную” цифру. Далее пользуются правилами вычислений с приближенными числами и правилами округления.
Контрольные вопросы
1. Как определяется величина систематической ошибки?
2. Как определяется величина случайной ошибки прямых измерений? На что указывает величина доверительного интервала?
3. Выразить доверительный интервал величины z, полученной при косвенных измерениях, через доверительные интервалы величин x, y, t, r, u, v, h, полученных в прямых измерениях для следующих зависимостей:
а) z = p r2 × h; б) z = r ( x2 – y2)/ t4( u2 – v2); в) z = x2× cos y.
4. Как изобразится на графике погрешность величины, отложенной вдоль оси абсцисс?
Список рекомендуемой литературы
1. Деденко Л.Г., Керженцев В.В. Математическая обработка и оформление результатов эксперимента. – М.: МГУ, 1977. – 112 с.
2. Сквайрс Дж. Практическая физика. – М.: Мир, 1971. – 248 с.
3. Физический практикум. Механика и молекулярная физика / Под ред. В.И. Ивероновой. – М.: Наука, 1967. – 352 с.
4. Лабораторный практикум по физике. Механика / Под. ред. А.А. Кулиша; Владим. политехн. ин-т. – Владимир, 1992. – 68 с.
5. Методические указания к лабораторным работам по физике. Молекулярная физика / Под ред. А.А. Кулиша; Владим. политехн. ин-т. – Владимир, 1992. – 40 с.
ОФОРМЛЕНИЕ ОТЧЕТА
Отчет студента по лабораторной работе составляется по следующей схеме: 1. Титульный лист. 2. Цель работы. 3. Оборудование. 4. Теоретическое введение. 5. Методика проведения эксперимента. 6. Экспериментальная часть. 7. Обработка результатов измерения. 8. Выводы.
Титульный лист оформляется на первой странице отчета. В центральной части этой страницы указываются номер лабораторной работы и ее название. Ниже (справа) фамилия исполнителя, номер группы и дата проведения измерений. В правом нижнем углу – три короткие строчки для подписи преподавателя: “к работе допущен”, “работа выполнена”, “работа защищена”. Со второй страницы следует описание остальных разделов отчета. Пункты 1 – 5 выполняются до начала выполнения лабораторной работы, пункт 6 – в лаборатории, пункты 7 – 8 после получения экспериментальных данных.
Теоретический материал, схемы, рисунки должны быть представлены в отчете в объеме, необходимом для осмысленного выполнения лабораторной работы. Рисунки и схемы выполняются с применением чертежных принадлежностей. Графики представляются на миллиметровой бумаге и вклеиваются в отчет.
По заочной форме обучения на выполнение лабораторных работ выделяется малый объем учебных аудиторных часов. Поэтому студентам-заочникам необходимо самостоятельно до начала занятий детально изучить описание лабораторной работы, используя дополнительно список рекомендуемой литературы. Качество своей подготовки студенты должны проверять, отвечая на контрольные вопросы. Домашняя самостоятельная подготовка студента-заочника “отражается” письменно в той части отчета, которая оформляется до начала выполнения лабораторной работы (пункты 1 – 5).
1. МЕХАНИКА
В лаборатории механики учащиеся применяют разнообразные измерительные инструменты в сочетании с действием автоматизированных установок. Лабораторные работы по механике направлены на освоение студентами методов статистической обработки данных физического эксперимента, методов исследования основных закономерностей поступательного и вращательного движения тел. Также изучаются свойства ряда важнейших механических величин.
Лабораторная работа № 1-1
Исследование распределения результатов физических измерений
Цель работы: определение параметров распределения результатов измерений и получение приближенного вида функции распределения.
Оборудование: микрометр, штангенциркуль, набор цилиндров.
Введение
Набор цилиндров (100 … 200 шт.), используемый в данной лабораторной работе – это совокупность одинаковых объектов, изготовленных в одинаковых условиях. Поэтому при измерении высоты (или диаметра) цилиндров, казалось бы, должна получаться одна и та же физическая величина. Однако в силу влияния большого количества причин, действующих случайно, совокупность высот цилиндров представляет собой набор случайных величин, моделирующих разброс результатов отдельных измерений в физическом эксперименте.
Это распределение характеризуется параметрами:
1) среднее арифметическое значение высоты 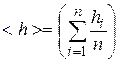 ;
;
2) дисперсия 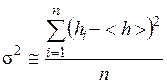 ;
;
3) среднеквадратичная погрешность 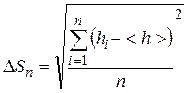 (где n – число измерений).
(где n – число измерений).
Если бы число измерений было бесконечно большим, то < h > совпадало бы с истинным значением высоты цилиндра, а D Sn c s. График распределения отдельных значений hi относительно < h > имел бы вид, подобный рис. 1. на с. 8. Число измерений ограничено, но и в этом случае удается получить приближенный вид функции распределения результатов измерений, построив гистограмму (столбчатую диаграмму).
Для построения гистограммы необходимо отрезок hmax – hmin (где hmax – максимальное из измеренных значений высот цилиндра, hmin – минимальное из измеренных значений высот цилиндра) разбить на N равных интервалов величины Dh, подсчитать число “попаданий” ni значений высот цилиндров в каждый интервал и относительную частоту попаданий в каждый интервал fi = ni / n .
Если значение высоты цилиндра попадает на границу интервалов, то этот цилиндр учитывается в правом интервале. Для количественного сравнения кривой Гаусса с гистограммой в последней по оси ординат необходимо отложить величину оценки плотности вероятности каждого интервала 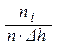 . Проделанные разбиения и расчеты в табличной форме имеют вид:
. Проделанные разбиения и расчеты в табличной форме имеют вид:
| Число интервалов | Интервал | ni | 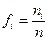
| ni/(n·Δh) |
| 1 | hmin ¸ h1 | n1 | f1 | f1/Δh |
| 2 | h1 ¸ h2 | n2 | f2 | f2/Δh |
| . | …………. | … | … | … |
| № | hN-1 ¸ hmax | nN | fN | fN/Δh |
 По значениям, представленным в таблице, строится гистограмма (см. рисунок). Как видно из рисунка, гистограмма – это совокупность прямоугольников, у которых одна сторона у всех равна ширине интервала Δh, а вторая – частоте попадания значений высот цилиндров в соответствующий интервал.
По значениям, представленным в таблице, строится гистограмма (см. рисунок). Как видно из рисунка, гистограмма – это совокупность прямоугольников, у которых одна сторона у всех равна ширине интервала Δh, а вторая – частоте попадания значений высот цилиндров в соответствующий интервал.
Порядок выполнения работы
1. Измерить высоты 100 … 200 цилиндров и результаты внести в отчет.
2. Определить по полученным значениям высот цилиндров: максимальное из измеренных значений высот цилиндров, минимальное из измеренных значений высот цилиндров, среднее значение высоты цилиндров, дисперсию распределения, среднеквадратичную погрешность распределения.
3. Разбить отрезок hmax – hmin на 6 ¸ 8 интервалов. Определить число попаданий и относительную частоту попаданий для каждого интервала. Полученные значения представить в табличной форме подобно таблице выше.
4. Построить гистограмму для распределения относительной частоты попаданий fi на миллиметровой бумаге.
5. Построить гистограмму оценки плотности вероятности ni/(n·Δh). Изобразить пунктиром там же Гауссову кривую по рассчитанным в п.2 значениям < h > и s2, воспользовавшись формулой 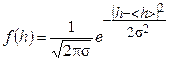 .
.
6. Сравнить Гауссову кривую с гистограммой оценки плотности вероятности и проанализировать полученные результаты.
Контрольные вопросы
1. Как построить гистограмму?
2. Чем определяется число интервалов, на которое разбивается отрезок hmax – hmin при построении гистограммы?
3. Как в эксперименте добиться того, чтобы гистограмма точнее отображала функцию распределения результатов эксперимента.








