Построение распределения для двух полос
По программе рассчитывается распределение интервалов t для заданного оператором числа nп полос. Расчет сводится к уменьшению в nп раз интервалов t. Результаты расчета берем из столбца файла, который обозначен символом tnпп, и следующего (справа) столбца со значениями вероятностей. Строим график распределения вероятностей интервалов в одном направлении движения (рис. 5).
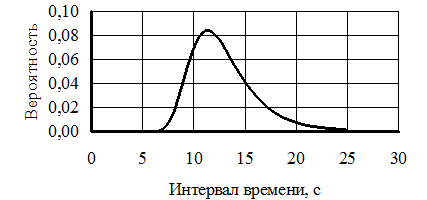
Рис. 5. Расчетное распределение интервалов по двум полосам
Слияние потоков
Рассмотрим, имеют ли место ограничения на интенсивность потока, входящего в обследованный поток.
Для расчета используем среднюю зависимость пространственных интервалов lп, м от скорости /1/, приведенную на рис. 6. Скорость V потока принимаем ориентировочно, по согласованию с преподавателем. По скорости V находим интервал lп, вычисляем временной интервал t, и по значениям s находим число вливающихся в поток автомобилей.
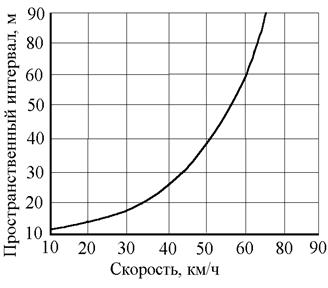
Рис. 6. Зависимость пространственных интервалов lП от скорости
Используем рассчитанные значения s накопленной вероятности, выведенные в конец файла rezpu.dat. Строим график функции s(V), показанный на рис. 7. Дополнительно составляем таблицу 4 со значениями интервалов t и вероятностями s.
Таблица 4
Распределение накопленной вероятности интервалов
| t | 12,5 | 13,1 | 13,8 | 14,7 | 15,6 | 16,6 | 17,8 | 19,2 | 20,8 |
| s | 0,0001 | 0,0004 | 0,0016 | 0,0048 | 0,0131 | 0,0321 | 0,0704 | 0,1388 | 0,2451 |
| t | 22,7 | 24,9 | 27,7 | 31,2 | 35,6 | 41,5 | 49,8 | 62,3 | 83,1 |
| s | 0,3881 | 0,5528 | 0,7130 | 0,8426 | 0,9283 | 0,9737 | 0,9925 | 0,9984 | 0,9997 |
Для используемого примера примем скорость потока V = 70 км/ч. Найден по графику (рис. 6) интервал: lп = 90 м. Вычислим временной интервал: t = 3,6 × lп/V = 3,6 × 90/70 = 4,6 с.
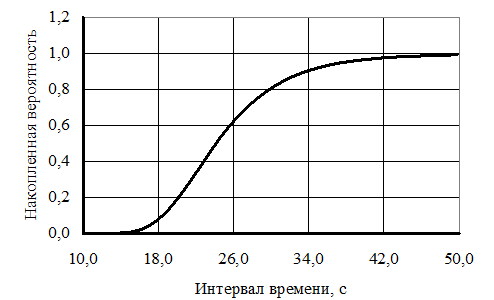
Рис. 7. Распределение накопленной вероятности интервалов
Получаем, что с большой вероятностью между любой парой автомобилей дополнительно может вместиться еще один автомобиль.
Выводы по работе
Обследованный поток имеет интенсивность движения 145 авт/ч и относится к свободному потоку уровня удобства A. Средний временной интервал t = 24,9 c. Экспериментальное распределение интервалов t удовлетворяет закону Пуассона. Законом Пуассона можно выразить распределение интервалов между автомобилями для потока интенсивностью 190 авт/ч, являющегося суммой двух потоков.
Автомобили движутся с большими интервалами t, и на процесс слияние потоков не накладываются ограничения.
3 ЛАБОРАТОРНАЯ РАБОТА №3
ИЗМЕРЕНИЕ И РАСЧЕТ ПАРАМЕТРОВ ТРАНСПОРТНОГО ПОТОКА ПО ЗАКОНУ ПИРСОНА
Цель работы: изучение методик измерения параметров транспортного потока и обработки результатов по закону Пирсона III типа.
Используемое оборудование: автомобиль-лаборатория, секундомеры.
Основные положения
Лабораторная работа №3 является продолжением работы №2, и в ней используются положения и параметры, выше изложенные в работе №2.
Для описания связанных потоков применяют закон распределения Пирсона III типа. По закону Пирсона вероятность p появления интервалов t, c между автомобилями описывается формулой:
p(t) = ak × e–a × t × tk–1/Г(k),
где k, a – коэффициенты функции; Г(k) – гамма функция. Дисперсия s и средний интервал tср выражаются через коэффициенты функции p(t) формулами: tср = k/a, s = k/a2. Значение гамма функции является в формуле константой, и вычисляется численным интегрированием:
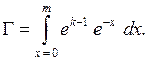
При интегрировании максимальное значение m переменной x обычно ограничивают величиной 50.
Распределение Пирсона обычно применяют при интенсивностях до 325 авт/ч (по одной полосе).
Методика измерения
Методика измерения включает 4 пункта, и отличается от методики, описанной в лабораторной работе №2, лишь тем, что закон Пирсона применяется для потоков, относящихся к уровням удобства Б и В.
Обработка сводки наблюдений
Обработка включает 3 пункта и аналогична методике, описанной лабораторной работе №2.
Определение диапазона изменения интервалов t.
По формуле (1) вычисляют среднее значение интервала tср. Минимальное значение диапазона принимают равно нулю. Максимальное значение принимают равно наибольшему интервалу t i и округляют в большую сторону до целого числа.
Разбиение диапазона на интервалы.
Первый участок диапазона (примерно 1/2 часть максимального значения диапазона) разбивают на небольшие интервалы (1 … 3 с), а второй участок – на интервалы в 2 раза больше (3 … 6 с). Начало и конец интервалов указывают в столбце 2 таблицы 5, средние значения времени tсj – в столбце 3, длины интервалов – в столбце 4.
В качестве примера в таблице 5 приведены данные, полученные на магистрали пр. Мира г. Омска, имеющей 4 полосы.
Расчет вероятностей. Расчет вероятностей и заполнение таблицы выполняются так же, как в лабораторной работе №2.
Таблица 5
Пример обработки сводки наблюдений
| j | tНj … tКj | tcj | Dt j | Aj | a j | p j |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 0 … 1 | 0,5 | 1 | 1 | 0,01 | 0,010 |
| 2 | 1 … 2 | 1,5 | 1 | 15 | 0,15 | 0,150 |
| 3 | 2 … 4 | 3 | 2 | 36 | 0,36 | 0,180 |
| 4 | 4 … 6 | 5 | 2 | 22 | 0,22 | 0,110 |
| 5 | 6 … 8 | 7 | 2 | 16 | 0,16 | 0,080 |
| 6 | 8 … 10 | 9 | 2 | 4 | 0,04 | 0,020 |
| 7 | 10 … 15 | 12,5 | 5 | 3 | 0,03 | 0,006 |
| 8 | 15 … 20 | 17,5 | 5 | 3 | 0,03 | 0,006 |
| Сумма | 100 | 1 |
Обработка результатов измерений
Строим график (рис. 8), отражающий экспериментальное распределение интервалов t j, используя значения tcj и p j.
Обрабатываем данные по программе obpir.exe (директория obpir). Для этого создаем файл isx.dat, записывая в него сначала число n интервалов, затем пары значений tcj и p j (см. пример – файл primer.dat). Файл isx.dat копируем в директорию obpir.
По программе вычисляется средний интервал tср и интенсивность движения l. Рассчитываются коэффициенты k , s и a, вычисляется средний интервал tср и отклонение S. Результаты обработки выводятся в файл rezpir.dat.
Рисунок 8 дополняем графиком расчетного распределения. Данные берем из файла rezpir.dat. Для используемого примера имеем:
tср = 4 c, l = 903 авт/ч, k = 3,07, a = 0,77, s = 5,17 с.
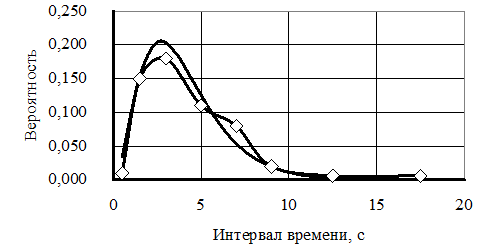
Рис. 8. Экспериментальное (à) и расчетное (––) распределение
интервалов по закону Пирсона
Получаем удовлетворительное соответствие расчетного распределения экспериментальному распределению (см. рис. 8), что подтверждается небольшим значением 0,0171 среднего отклонения S.








