Методика измерения
Методика измерения включает 4 пункта.
Выбор участка дороги. Закон Пуассона применяется для потоков, относящихся к уровню удобства A. Измерения выполняют на дорогах, имеющих 4 … 6 полос. Интервалы измеряют на одной полосе. Полосу дороги и сечение выбирают в соответствии с решаемыми задачами ОДД. При выполнении лабораторной работы они указываются преподавателем. Число замеров N обычно принимают равно 100.
Обеспечение случайного порядка измерений. Для исключения систематических погрешностей измеряют, например, интервал между автомобилем, находящимся ближе всех к сечению, и следующим за ним автомобилем.
Подготовка сводки наблюдений. Сводка наблюдений представляет собой таблицу, имеющую три столбца. В столбцы записываются номер пары автомобилей, интервал времени и диапазон, в котором располагается интервал.
Выполнение замеров. При прохождении через сечение бампера первого автомобиля пары запускают секундомер, и останавливают его при прохождении второго автомобиля. Записывают номер пары и интервал t i в сводку наблюдений. Повторяют измерения до достижения числа замеров N.
Обработка сводки наблюдений
Обработка включает 3 пункта.
Определение диапазона изменения интервалов t.
По формуле (1) вычисляют среднее значение интервала tср. Минимальное значение диапазона принимают равно tср/2. Максимальное значение принимают равно наибольшему интервалу t i, и округляют в большую сторону до целого числа.
Разбиение диапазона на интервалы.
Пусть tНj и tКj начало и конец интервала номер j. Поскольку функция распределения является нелинейной, то применяют интервалы разной величины. В начале и конце диапазона используют большие интервалы (5 … 10 с), а в середине диапазоны величину интервалов берут меньше (2 … 4 с). Общее число интервалов не должно превышать 20. Начало и конец интервалов указывают в столбце 2 таблицы 3. Средние значения времени tсj = (tНj + tКj)/2 на интервалах записывают в столбец 3, длины интервалов Dtj = tКj – tНj записывают в столбец 4 таблицы.
В качестве примера в таблице 3 приведены данные, полученные на междугородней дороге, имеющей 4 полосы.
Расчет вероятностей.
В сводке наблюдений находят автомобили, для которых интервалы t i располагаются в диапазонах Dtj: ti > tНj, ti £ tКj. Заполняют столбец 3 сводки. Подсчитывают частоты Aj, и записывают их в столбец 5 таблицы 3. Контролируют сумму частот (она равна N). Вычисляют частости a j = Aj/N, заполняют столбец 6 таблицы 3. Вычисляют вероятности p j = a j/Dtj, и заполняют столбец 7 таблицы 3.
Таблица 3
Пример обработки сводки наблюдений
| j | tНj … tКj | tcj | Dt j | Aj | a j | p j |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 10 … 15 | 12,5 | 5 | 1 | 0,01 | 0,002 |
| 2 | 15 … 20 | 17,5 | 5 | 15 | 0,15 | 0,020 |
| 3 | 20 … 23 | 21,5 | 3 | 36 | 0,36 | 0,097 |
| 4 | 23 … 26 | 24,5 | 3 | 22 | 0,22 | 0,080 |
| 5 | 26 … 29 | 27,5 | 3 | 16 | 0,16 | 0,053 |
| 6 | 29 … 32 | 30,5 | 3 | 4 | 0,04 | 0,043 |
| 7 | 32 … 37 | 34,5 | 5 | 3 | 0,03 | 0,008 |
| 8 | 37 … 42 | 39,5 | 5 | 3 | 0,03 | 0,004 |
| 9 | 42 … 50 | 46 | 8 | 0,0013 | ||
| Сумма | 100 |
Обработка результатов измерений
Строим график (рис. 4), отражающий экспериментальное распределение временных интервалов, используя значения tcj и p j.
Обрабатываем данные по программе obpua.exe, которая находится в директории obpuac. Для этого создаем файл isx.dat, записывая в него сначала число n интервалов, затем пары значений tcj и p j (см. пример – файл primer.dat). Для составления файла используем редактор Блокнот. Программа позволяет вводить данные вручную и редактировать их.
Результаты обработки выводятся программой в файл rezpu.dat. По программе вычисляется средний интервал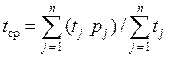 
и интенсивность движения l по формуле (1), рассчитывается поправка m. Вычисляется среднее квадратичное отклонение S расчетных данных от экспериментальных данных.
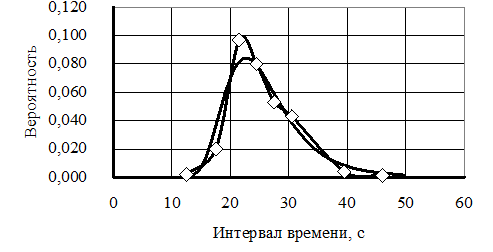
Рис. 4. Экспериментальное (à) и расчетное (––) распределение интервалов
Рисунок 4 дополняем расчетным распределением. Данные берем из столбца файла, который обозначен символом t1п и крайнего (справа) столбца со значениями вероятностей p.
Для используемого примера имеем: tср = 24,9, m = 1,126, l = 145, S = 0,0096. Экспериментальное распределение соответствует расчетному (см. рис. 4), что подтверждается небольшим значением отклонения S.