Обработка сводки наблюдений
Обработка включает 4 пункта.
Определение диапазона изменения скоростей. Находят максимальное Vmax значение скорости в сводке и округляют его в большую сторону с шагом 10 км/ч. Минимальное значение принимают равно нулю.
Разбивка диапазона на интервалы VНj … VКj. Диапазон скоростей разбивают на интервалы VНj … VКj. Например: 0-40, 40-50, 50-60, …, 100-110 (Vmax = 110).
Заполнение таблицы и расчет вероятностей. Заполняют столбцы 1 и 2 таблицы 1. Вычисляют средние скорости VСj на интервалах и заполняют столбец 3 таблицы. Находят длины DV j интервалов, записывают их в столбец 4 таблицы.
Подсчитывают автомобили, скорости которых располагается в интервалах DV j: V i > VНj, V i £ VКj. Заполняют столбец 3 сводки наблюдений. Подсчитывают частоты Aj, и записывают их в столбец 5 таблицы. Контролируют сумму частот (она равна N).
Вычисляют вероятности. Сначала вычисляют частости a j и заполняют столбец 6 таблицы. Контролируют сумму частостей (сумма равна 1). Вычисляют накопленные частости s j, заполняют столбец 7. Затем вычисляют вероятности p j, и заполняют столбец 8.
Таблица 1
Пример обработки сводки наблюдений
| j | VНj … VКj | Vcj | DV j | Aj | a j | s j | p j |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 0 … 40 | 20 | 40 | 2 | 0,02 | 0,02 | 0,0005 |
| 2 | 40 … 50 | 45 | 10 | 6 | 0,06 | 0,08 | 0,006 |
| 3 | 50 … 60 | 55 | 10 | 20 | 0,20 | 0,28 | 0,020 |
| 4 | 60 … 70 | 65 | 10 | 36 | 0,36 | 0,64 | 0,036 |
| 5 | 70 … 80 | 75 | 10 | 22 | 0,22 | 0,86 | 0,022 |
| 6 | 80 … 90 | 85 | 10 | 10 | 0,10 | 0,96 | 0,010 |
| 7 | 90 … 100 | 95 | 10 | 4 | 0,04 | 1,00 | 0,004 |
| Сумма | 100 | 1 |
Обработка результатов измерений
Строят график p = f(V) экспериментального распределения скоростей (рис. 1), используя значения Vcj и p j.
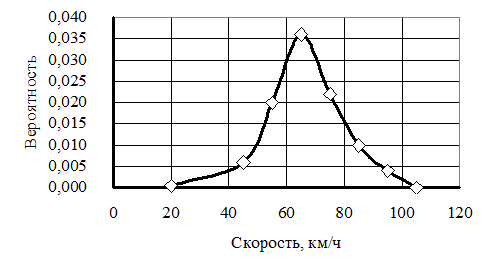
Рис. 1. Экспериментальное распределение скоростей
Экспериментальные данные обрабатывают по программе normr.exe. Данные записывают в файл isx.dat (в директории obnz имеется пример – файл primer.dat). Сначала записывают число n интервалов, затем пары значений Vcj и p j. Для составления файла используют редактор Блокнот. Программа позволяет вводить данные вручную и редактировать их.
Обработка данных по программе включает два шага.
На первом шаге рассчитываются параметры Vср и s, вычисляются вероятности pрj и накопленные вероятности sрj для скоростей Vc, нарастающих с шагом 5 км/ч.
На втором шаге из исходных данных исключают вклад, вносимый дисциплинированными водителями, и снова рассчитываются параметры Vср и s. Для исключения оператор задает отрицательное значение p j, обычно соответствующее скорости Vср = 65 км/ч. Повторно вычисляются вероятности pкj и накопленные вероятности sкj. Результаты расчетов выводятся в файл reznz.dat.
Для рассматриваемого примера (ул. Волгоградская, г. Омск) получаем на первом шаге Vср = 66,0 км/ч, s = 11,6 км/ч, среднее отклонение S = 0,002. Берем из файла исходные данные, рассчитанные вероятности, и заполняем столбцы 2 … 6 таблицы 2.
На втором шаге опускаем значение 0,036 при j = 4. Получаем иные параметры: Vср = 66,3 км/ч, s = 13,4 км/ч, S = 0,0015. Берем из файла рассчитанные вероятности, заполняем столбцы 7, 8 таблицы 2.
Таблица 2
Распределение скоростей автомобилей
| j | Vcj | p j | s j | pрj | sрj | pкj | sкj |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 20 | 0,0005 | 0,02 | 0,000 | 0,000 | 0,000 | 0,001 |
| 2 | 45 | 0,0060 | 0,08 | 0,007 | 0,055 | 0,008 | 0,079 |
| 3 | 55 | 0,0200 | 0,28 | 0,022 | 0,231 | 0,021 | 0,254 |
| 60 | 0,030 | 0,381 | 0,027 | 0,387 | |||
| 4 | 65 | 0,0360 | 0,64 | 0,034 | 0,552 | 0,030 | 0,535 |
| 70 | 0,032 | 0,713 | 0,029 | 0,679 | |||
| 5 | 75 | 0,0220 | 0,86 | 0,025 | 0,841 | 0,024 | 0,800 |
| 80 | 0,017 | 0,924 | 0,018 | 0,888 | |||
| 6 | 85 | 0,0100 | 0,96 | 0,009 | 0,969 | 0,011 | 0,944 |
| 90 | 0,004 | 0,989 | 0,006 | 0,976 | |||
| 7 | 95 | 0,0040 | 1,00 | 0,002 | 0,997 | 0,003 | 0,991 |
| 100 | 0,000 | 0,999 | 0,001 | 0,997 |
На рисунке 2 изображаем два распределения pр = f(V) и pк = f(V) по скорости. На рисунке 3 изображаем два графика sр = f(V) и sк = f(V) для накопленной вероятности.
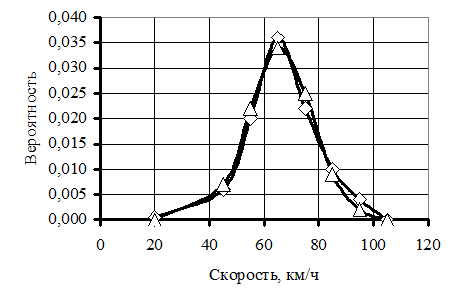
Рис. 2. Распределения вероятностей скоростей: D – pр, à – pк
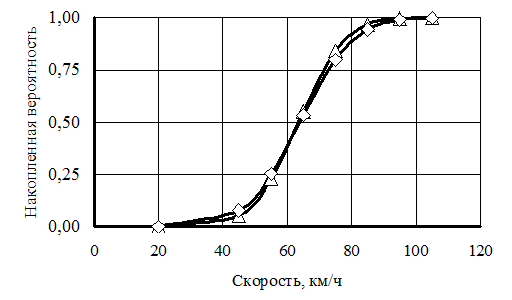
Рис. 3. Распределения накопленных вероятностей скоростей:
D – sр, à – sк
Анализ результатов
Анализ результатов включает 3 пункта.
Оценка соблюдения водителями правил дорожного движения (ПДД) по скорости.
Графики на рис. 1 и рис. 2 не имеют существенных различий. Среднее квадратичное отклонение расчетных и экспериментальных данных небольшое: S = 0,002. Следовательно, фактическое распределение скоростей удовлетворяет нормальному закону. Автомобили движутся так же, как в свободном потоке, скорость потока равна 65 км/ч. Действия водителей сводятся поддержанию среднего значения скорости, а не к ограничению ее величиной 70 км/ч.
Скорость 60 км/ч превышают 62% водителей (Vc = 60, sр = 0,381, см. табл. 2). Наибольшую (формально разрешенную) скорость 70 км/ч превышают 29% водителей (Vc = 70, sр = 0,713). Скорость 90 км/ч превышают 1,1% водителей (см. Vc = 90, sр = 0,989), которые создают опасные ситуации.
Расчет числа дисциплинированных водителей.
По таблице 2 находим частоту для водителей, специально выдерживающих скорость в диапазоне 60 … 70 км/ч:
DV4 (p4 – pк4) = 10 × (0,036 – 0,03) = 0,06.
Получаем: 6% водителей намеренно выдерживают скорость в диапазоне DV4.
Назовем условно «свободными» водителями тех водителей, которые поддерживают среднее значение скорости. Доля таких водителей составляет (1 – 0,06) × 100 = 94%. По таблице 2 находим: скорость 70 км/ч превышают 32% «свободных» водителей (Vc = 70, sк = 0,679), из них скорость 90 км/ч превышают 2,4% (Vc = 90, sр = 0,976).
Эффективность контроля скорости службой ГИБДД.
Контроль скоростей движения на магистрали считаем неудовлетворительным, так как 29% водителей нарушают правила ПДД.
2 ЛАБОРАТОРНАЯ РАБОТА №2
ИЗМЕРЕНИЕ И РАСЧЕТ ПАРАМЕТРОВ ТРАНСПОРТНОГО ПОТОКА ПО ЗАКОНУ ПУАССОНА
Цель работы: изучение методик измерения параметров транспортного потока и обработки результатов по закону Пуассона.
Используемое оборудование: автомобиль-лаборатория, секундомеры.
Основные положения
В транспортном потоке автомобили движутся с разными временными интервалами t, с между автомобилями. Движение потока отражает средний интервал tср. Средний интервал tср связан с интервалами t i и интенсивностью потока l, авт/ч формулами:
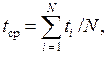
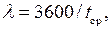 (1)
(1)
где N – число замеров.
Число автомобилей n, проходящих через сечение дороги за время t, c, зависит от интенсивности движения: n = t/tср. Параметры потока n и t являются случайными величинами. Распределения их значений описываются законами, разработанными в теории вероятностей. Однако не существует универсальных законов, описывающих распределения с приемлемой точностью при различной интенсивности l. Поэтому при решении практических задач организации движения (ОДД) используют разные законы, а также их комбинации.
Распределение Пуассона часто применяется в практике. Закон Пуассона описывает вероятность p прохождения n автомобилей через сечение дороги за время измерения t. Функция распределения p(n) выражается формулой:
p(n) = e–l × t × (l × t)n/n!,
где n! = 1 × 2 × … × n, (0! = 1).
В формулу подставляют целые числа n и рассчитывают вероятность p. Размерность времени измерения приводят к часам. По значениям n находят интервалы t =t/n и получают функцию p(t) распределения временных интервалов t.
Вычисляют интегралы функции p(t) для различных значений интервала t и получают функцию s(t) накопленной вероятности s. Функция s(t) описывает вероятность прохождения через сечение дороги автомобилей, движущихся с интервалами менее или равно t.
Распределение Пуассона справедливо при небольших интенсивностях движения l до 100 авт/ч (по одной полосе). Для расширения области применения закона применяют поправку m:
p = e–m × l × t × (m × l × t)n/n!,
где m » 0,5 … 1,5. Значение m задает смещение функции в сторону больших (m < 1) или меньших (m > 1) интервалов.
Распределение Пуассона с поправкой применяют при интенсивности движения до »150 авт/ч (по одной полосе).








