Представляет большой интерес вывод времени релаксации из условий стационарного необратимого, процесса- например, из условий стационарного течения вязкой среды.
Этот случай был рассмотрен в пункте 2 параграфа 4. Там было установлено, что при стационарном течении вязкой среды величина тангенциального упругого напряжения сдвига в каждой точке среды остается неизменной во времени и равной
δ=ⴄ 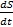 =ⴄ
=ⴄ 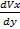
При этих условиях в среде существует запас потенциальной энергии упругого напряжения сдвига δ.
Если взять простейший случай, когда δ не только постоянно во времени, но и одинаково во всех точках среды, т.е. когда градиент скорости, перпендикулярный к потоку dVx/dy=const.., то объемная плотность упругой энергии текущей среды (см. формулу 15 §5).
Uупр= 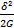
С другой стороны, легко доказать, что энергия, рассеиваемая ежесекундно в 1 см³ среды, т.е. мощность диссипативного процесса.
Wдисс= 
Целесообразно вывести новую меру «сопротивления» упруго-вязкой среды диссипативному процессу, измеряемую отношением Uупр /Wдисс.
Чем больше плотность упругой энергии Uупр и чем меньше отвечающая ей Wдисс, тем больше указанное «сопротивление среды».
Легко, однако, убедиться в том, что это «сопротивление диссипации энергии» не что иное, как время релаксации для упругой энергии. Действительно:
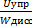 =
= 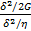 =
= 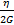 =τэн=
=τэн=  τδ
τδ
(см. формулу 16 §5)
Из формулы (19) вытекает новое определение понятия времени релаксации энергии τэн и напряжения τδ , устанавливаемое на основе стационарного диссипативного процесса.
Согласно формуле (19), время релаксации для энергии τэн равно отношению плотности упругой энергии и мощности энергии, рассеиваемой в см³/сек в данной среде при U = const .
Величина времени релаксации τδ равна удвоенной величине только что названного отношения.
Введенное нами понятие «сопротивляемости диссипативному процессу» Uупр/Wдисс совпадает с понятием времени релаксации только для простейшего типа процессов, для которых Uупр/Wдисс=const.,т.е. для таких процессов, для которых величина рассеяния энергии прямо пропорциональна упругой энергии, или, говоря более широко, величине энергетического отклонения среды от равновесного состояния. Мы встретимся в других разделах курса с примерами именно таких процессов (например, ток в металлическом проводнике; обладающем сопротивлением).
Однако перед нами возникнут и другие, более общие и сложные случаи, при которых величина Wдисс не является прямо пропорциональной Uупр. Эти процессы, выходящие из пределов теории Максвелла, могут называться нелинейными релаксационными процессами.
§7. Релаксационные представления и жидкость
Ещё сравнительно недавно большинство физиков и физико-химиков придерживались той старой точки зрения, что жидкости отличаются от твердых тел отсутствием упругости по отношению к сдвигу.
Относящиеся сюда старые и новые представления будут рассматриваться нами в разделе «Молекулярная физика».
Сейчас нам необходимо рассмотреть выдвинутый вопрос только с точки зрения релаксационной картины, пока, ничего не говоря о молекулярной стороне поставленного вопроса.
Объёмная упругость жидкостей вблизи точки плавления незначительно отличается от объёмной упругости соответствующих твёрдых тел. Это значит, что для того, чтобы сжать объём жидкости на определенную долю (например, на 1%), необходимо давление, лишь немногим отличающееся от того, которое необходимо приложить к твердому телу для того, чтобы произвести такую же относительную деформацию объёма.
Отсюда следует, что силы, действующие между частицами жидкости и твёрдого тела, лишь немного различаются вблизи температуры плавления. Так как время релаксации τ=  ? то коэффициент вязкости ⴄ= G·τ/
? то коэффициент вязкости ⴄ= G·τ/
Для маловязких жидкостей, таких, как вода, спирты, ⴄ= 0,01 пауза или даже меньше (см. §3.)
Из только что написанной формулы следует, что низкое значение ⴄ, т.е. высокая текучесть жидкостей, может обуславливаться либо малой величиной модуля сдвига G , либо малой величиной времени релаксации τ.
В XIX и в начале XX века большинство физиков стояло на первой из указанных точек зрения, т.е. полагало, что для жидкостей G очень мало.
Однако это положение было трудно согласовать со всеми другими свойствами жидкостей, из которых вытекало, что межмолекулярные силы в жидкостях мало отличаются от их величины в твердых телах.
Упомянутое малое различие объёмных упругостей для жидкого и твёрдого состояния у одного того же вещества- это лишь одно из подобных свойств.
В результате за последние десятилетия возникла и окрепла, в особенности благодаря трудам советских ученых, современная теория жидкого состояния, базирующаяся на второй точке зрения: у жидкостей величина модуля сдвига G, мало отличается от той же величины величины для твёрдых тел.
Однако время релаксации τ для твёрдых тел очень велико, и иногда τ→ꝏ, тогда как для таких легколетучих жидкостей, как вода, оно имеет порядок 10ˉ1³ сек.
Модуль сдвига G твёрдых тел имеет порядок величины 1011, 1012 дин/cм2 (см. таблицу)
| Вещество | G дин/см2 |
| Al | 2,67·1011 |
| Au | 2,77·1011 |
| Cu | 4,55·1011 |
| Pt | 6,10·1011 |
| Ag | 2,87·1011 |
| Сталь | 8,12·1011 |
| Стекло | 2,6-3,2·1011 |
| Крон | 2,6-3,2·1011 |
| Флинт | 2,0-2,5·1011 |
Отсюда именно и следует, что время релаксации τ для маловязких жидкостей τ=G/ⴄ очень мало.
В случае расплавленных стёкол и жидких высокополимеров при понижении температуры время релаксации τ быстро возрастает. В особенности быстро растет время при процессе переохлаждения. В то же время величина модуля сдвига с понижением температуры также растет, однако изменение её очень незначительно.
Для многих высокополимеров и стекол величина времени релаксации в области переохлаждения изменяется на протяжении нескольких десятков градусов в десятки и сотни миллионов раз.
Опыт показывает, что стекло становится твёрдым при той температуре, при которой величина его вязкости достигает 1013 пуаз.
Если исходить из приведённых в таблице значений модуля сдвига 2,5·1011 дин/см2 для стекла, то можно сделать заключение, что при охлаждении стеклорасплава до его отвердевания (застеклование) время релаксации возрастает до
τ=  =1013/2,5·1011=40 сек.
=1013/2,5·1011=40 сек.
1958 год март.








