Она равна времени, за которое начальное напряжение убывает в («е») раз, и представляет собою отношение коэффициента вязкости ⴄ к модулю сдвига G .

Дата: 2025-05-01; Просмотры: 2

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

3. Переход к частному случаю релаксации напряжения при постоянной величине деформации

Если вязко-упругую среду подвергнуть деформации, остающейся неизменной по свой величине (S=const), то при конечной величине вязкости, т.е. при ⴄ≠ꝏ, будет наблюдаться процесс релаксации упругого напряжения, при котором начальная величина напряжения, обусловленная заданной величиной деформации, постепенной уменьшатся (релаксирует), асимптотически стремясь к нулю.

Исследуем закон ослабления величины напряжения в функции от времени.

Для этого вообразим, что участок упруго-вязкой среды АВСД подвергнут деформации сдвига

S= 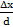= const, т.е., что точки приложения силы F закреплены неподвижно (рис.6)/

В этом случае, отвечающая заданной деформации S= 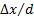начальная величина ( в момент времени t=0) сдвигового напряжения δ̊=GS подвергается релаксации.

Следует, однако, заметить, что и при всякого рода других деформациях, например, при деформации сжатия или растяжения за счет сил F-F или F ́-F ́(рис.7) в реальном упруго-вязком теле также будет происходить релаксация нормальных и тангенциальных напряжений.

Как показывает теория упругости, при деформации сжатия или растяжения в теле возникает, помимо нормального упругого напряжения, также и тангенциальная (сдвиговая) деформация и отвечающая ей величина тангенциального напряжения.

Эти нормальные и тангенциальные упругие напряжения взаимно связаны по законам теории упругости.

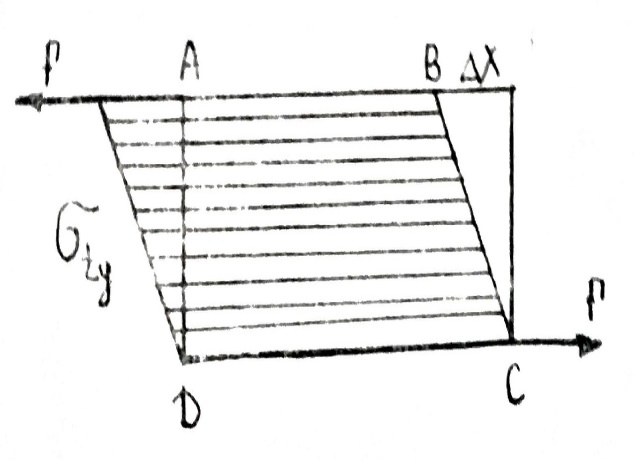
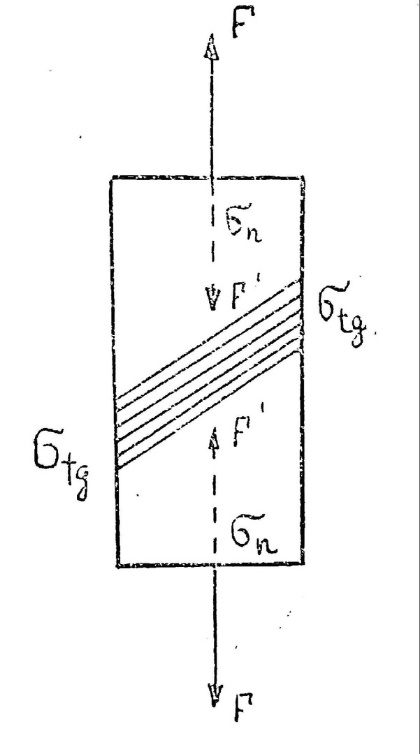
Рис. 6. Рис. 7.

Реологические свойства упруго-вязкой среды, т.е. среды с конечной (а не бесконечно большой) величиной коэффициента вязкости, проявляются в том, что благодаря наличию какой-то степени текучести происходит релаксация тангенциальных, т.е. сдвиговых напряжений. Но из этого следует, что данное условие текучести (ⴄ≠ꝏ) достаточно и для релаксации всех других (например, нормальных) составляющих тензора упругого напряжения, т.к. все составляющие напряжения, как нормальные, так и тангенциальные, взаимно связаны.

Рассмотрим уравнение Максвелла (12)

При S= const , т.е. при 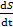=0

Уравнение (12) принимает для этого важного частного случая вид

0= · +

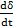Или

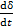- = δ (13)

Т.е. скорость убыли или скорость величины тангенциального напряжения (- dδ / dt ) в любой момент времени прямо пропорциональна действующей в этот момент величине напряжения δ.

Таково выражение дифференциального закона для релаксации в упруго-вязкой среде по Максвеллу.

Из уравнения (13) легко найти зависимость упругого напряжения δ, как явную функцию времени, т.е. найти решение дифференциального уравнения (13).

Оно имеет вид

δ=δ ̥e^{- ·t} (14)

Легко убедиться, что это так, если из уравнения (14) найти производную δ по времени t.

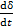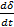= -δ · е^{- ·t}= - ·δ или - = - δ;

т.е. из (14) снова получается уравнение (13). Следовательно, уравнение (14) является решением или, как говорят, интегралом дифференциального уравнения (13).

Закон, выражаемый уравнением (14), есть закон экспоненциального изменения величины упругого напряжения со временем t.

Он представлен графически на рис. 8.

Из формулы (14) следует, что начальная величина напряжения убывает в «е» раз (т. Е. в 2,718 . . . раза) за время t=τ= .

Действительно, если положить, что от начала деформации протекло время, равное τ=ⴄ/G сек, ( вспомним, что (ⴄ) выражается в 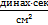, а (G)- в 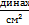, то уравнение (14) превращается в следующее

δ_τ = δ ̥е^-1= =

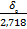
Мы видим, что упругое напряжение релаксирует тем менее, чем больше величина τ= , называемая временем релаксации.

Она равна времени, за которое начальное напряжение убывает в («е») раз, и представляет собою отношение коэффициента вязкости ⴄ к модулю сдвига G .

Таким образом, релаксация протекает тем быстрее, чем больше упругость среды.

В деформированной упругой среде имеется запас потенциальной упругой энергии.

На лекции о потенциальной энергии мы узнали, что для среды,

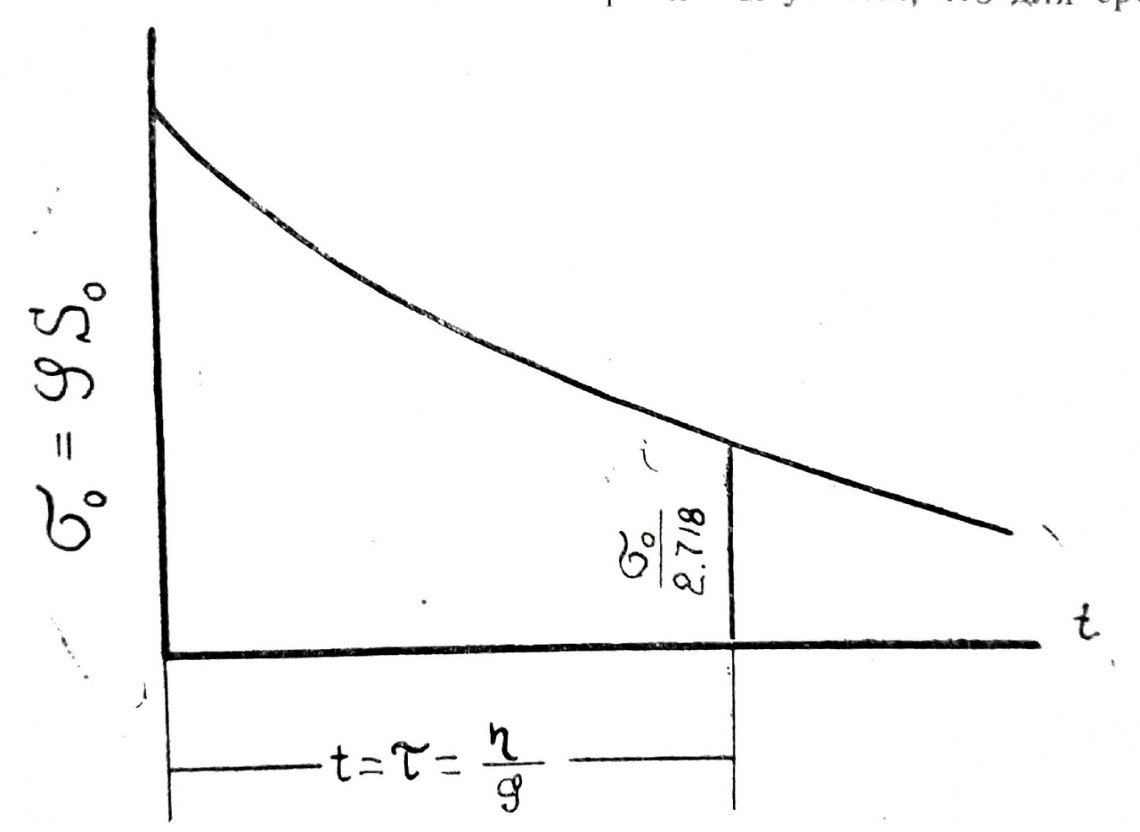
Рис. 8.

подчиняющейся закону Гука, упругая потенциальная энергия U_pot выражается формулой

U_pot =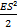

Для деформации растяжения или сжатия.

Соответственно, для деформации сдвига она будет равна

U_упр =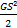

Но т.к. по закону Гука S²= 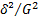, то

U_упр= 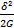(15)

Это выражение показывает, что при заданной величине напряжения сдвига упругая энергия прямо пропорциональна квадрату упругого напряжения и обратно пропорциональна модулю сдвига.

В абсолютной системе (см· г· сек) величины δ и G выражаются в динах·смˉ².

Поэтому величина Uупр. тоже должна выражаться в динах·смˉ².

= =

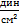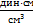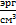
Таким образом величина Uупр в формуле (15) показывает, какова энергия упругой деформации, заключенной в единице объёма среды.

Эту величину иногда называют объёмной плотности упругой энергии деформации сдвига.

Пользуясь этой формулой и законом релаксации напряжения (формула 14), найдём закон для релаксации энергии упругой деформации.

Из формулы (14) следует, что

δ²=δ ̥²·е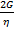^{- ·t}

А на сновании формулы (15) теперь можем написать

U_pot= 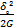·e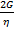^{- ·t}= U⁰_pot·e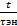^- (16)

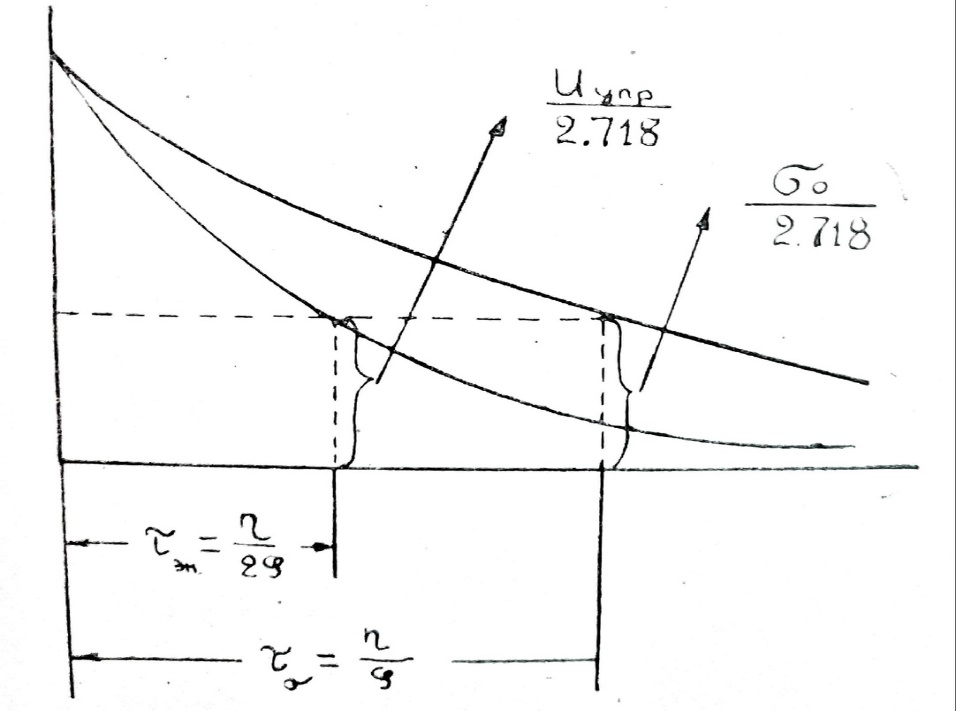
Рис. 9.

Этот последний результат показывает, что упругая энергия как величина, пропорциональна квадрату упругого напряжения, релаксирует быстрее, чем само напряжение.

При этом время релаксации для упругой энергии τэн= 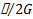вдвое меньше, чем время релаксации для напряжения τδ= .

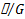τ_эн= τ_δ (17)

τ_эн- есть время, за которое запас потенциальной энергии в упруго-вязкой среде убывает в е-2,718 . . . раза.

Это время вдвое меньше того, за которое в 2,718 раза убывает упругое напряжение.

Это соотношение изображено на рис.9 (стр.16).

Очень важно подчеркнуть, что релаксация упругой энергии в упруго-вязкой среде есть типичный приме диссипативного процесса, при котором рассеяние упругой энергии происходит за счет работы сил внутреннего трения. При этом убыль упругой энергии измеряется количеством теплоты q, выделяющейся при работе сил трения.

Из уравнения (15) и (16) следует, что

Q=U⁰_упр- U^t_pot= 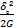- 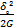·е 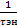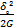^- = (1- е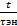^- ) (18)

§5. Обратимые и необратимые процессы в механике

Наличие диссипации энергии с необратимостью процессов в механических системах.

Понятие о необратимых процессах вообще вводится в термодинамике. Оно будет затрагиваться нами далее в разделе курса «Молекулярная физика и термодинамика». Однако сейчас нам следует обратить внимание на частный случай необратимых процессов, а именно процессов, сопровождаемых диссипацией энергии.