Критерии согласия для проверки гипотез
Критерии согласия применяются для проверки гипотезы о законе распределения исследуемой случайной величины. Во многих практических задачах точный закон распределения неизвестен. Поэтому выдвигается гипотеза о соответствии имеющегося эмпирического закона, построенного по наблюдениям, некоторому теоретическому. Данная гипотеза требует статистической проверки, по результатам которой будет либо подтверждена, либо опровергнута.
Критерий согласия Пирсона - χ2 – один из основных, который можно представить как сумму отношений квадратов расхождений между теоретическими и эмпирическими частотами к теоретическим частотам:
χ2 = 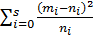
- s – число групп, на которые разбито эмпирическое распределение,
- mi – наблюдаемая частота признака в i-й группе,
- ni – теоретическая частота.
Для распределения χ2 составлены таблицы, где указаны критические значения критерия согласия χ2 для выбранного уровня значимости α и степеней свободы k.
Число степеней свободы k определяется как число групп в ряду распределения (s) минус число связей: k = s – r. Под числом связей понимается число показателей эмпирического ряда, использованных при вычислении теоретических частот, т.е. показателей, связывающих эмпирические и теоретические частоты. Например, при выравнивании по кривой распределения Эрланга или нормального распределения имеется три связи. Поэтому число степеней свободы определяется как k = s – 3. Для распределения Пуассона число k = s – 2.
При полном совпадении теоретического и эмпирического распределений
χ2 = 0, в противном случае χ2 > 0. Если χ2расч > χ2табл, то при заданном уровне значимости и числе степеней свободы гипотезу о несущественности (случайности) расхождений отклоняем. В случае, если χ2расч< χ2табл гипотезу принимаем и с вероятностью Р можно утверждать, что расхождение между теоретическими и эмпирическими частотами случайно.
Пример. Проверим гистограмму, полученную в занятии 9 для 9-и канального устройства, на соответствие распределению Эрланга. В данном случае число групп в ряду распределения (число интервалов гистограммы) равно 10. Поэтому эмпирические и расчётные данные сводим в таблицу 1.
Таблица 1
| i | Pi | ni | mi | ni - mi | (ni - mi)2 | (ni - mi)2/ni |
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| 5 | ||||||
| 6 | ||||||
| 7 | ||||||
| 8 | ||||||
| 9 | ||||||
| 10 | ||||||
| χ2 = Σ |
Эмпирические данные для данной таблицы mi берутся непосредственно из отчёта модуля 9. Расчётные значения вычисляются как ni = Pi * N, где Pi определяется по формуле Эрланга (можно воспользоваться программой erlangcalc), а N соответствует длине прогона (число, устанавливаемое при команде Start).
После этого проверяется гипотеза по таблице 2 о соответствии гистограммы распределению Эрланга. В нашем случае число степеней свободы
k = s – 3 =10 – 3 = 7. Пусть в результате расчета по таблице 1 оказалось, что χ2 = 2,5. Тогда по таблице 2 для k = 7 находим, что 2.17< χ2<2.83, и делаем вывод о том, что с вероятностью Р, лежащей между 0.9 и 0.95, гипотеза о соответствии эмпирического распределения распределению Эрланга является правдоподобной.
Таким образом, любой критерий согласия не подтверждает однозначно правильность гипотезы о законе распределения исследуемой случайной величины. Критерий лишь определяет вероятность правильности гипотезы. А при проверке нескольких гипотез (например, соответствие эмпирического распределения нормальному или эрланговскому) можно принять более вероятную.
Таблица 2. Значения квантили χα2 в зависимости от уровня вероятности и числа степеней свободы k
| k | Вероятность P(χ2 > χα2) | ||||||||
| 0.99 | 0.95 | 0.90 | 0.7 | 0.50 | 0.3 | 0.10 | 0.05 | 0.01 | |
| 1 | 0.00016 | 0.0039 | 0.016 | 0.148 | 0.455 | 1.074 | 2.71 | 3.84 | 6.63 |
| 2 | 0.020 | 0.103 | 0.211 | 0.713 | 1.39 | 2.41 | 4.61 | 5.99 | 9.21 |
| 3 | 0.115 | 0.352 | 0.584 | 1.424 | 2.37 | 3.66 | 6.25 | 7.81 | 11.3 |
| 4 | 0.297 | 0.711 | 1.06 | 2.20 | 3.36 | 4.88 | 7.78 | 9.49 | 13.3 |
| 5 | 0.554 | 1.15 | 1.61 | 3.00 | 4.35 | 6.06 | 9.24 | 11.1 | 15.1 |
| 6 | 0.872 | 1.64 | 2.20 | 3.83 | 5.35 | 7.23 | 10.6 | 12.6 | 16.8 |
| 7 | 1.24 | 2.17 | 2.83 | 4.67 | 6.35 | 8.38 | 12.0 | 14.1 | 18.5 |
| 8 | 1.65 | 2.73 | 3.49 | 5.53 | 7.34 | 9.52 | 13.4 | 15.5 | 20.1 |
| 9 | 2.09 | 3.33 | 4.17 | 6.39 | 8.34 | 10.66 | 14.7 | 16.9 | 21.7 |
| 10 | 2.56 | 3.94 | 4.87 | 7.27 | 9.34 | 11.78 | 16.0 | 18.3 | 23.2 |
| 11 | 3.05 | 4.57 | 5.58 | 8.15 | 10.3 | 12.90 | 17.3 | 19.7 | 24.7 |
| 12 | 3.57 | 5.23 | 6.30 | 9.03 | 11.3 | 14.01 | 18.5 | 21.0 | 26.2 |
| 13 | 4.11 | 5.89 | 7.04 | 9.93 | 12.3 | 15.12 | 19.8 | 22.4 | 27.7 |
| 14 | 4.66 | 6.57 | 7.79 | 10.82 | 13.3 | 16.22 | 21.1 | 23.7 | 29.1 |
| 15 | 5.23 | 7.26 | 8.55 | 11.72 | 14.3 | 17.32 | 22.3 | 25.0 | 30.6 |
| 16 | 5.81 | 7.96 | 9.31 | 12.62 | 15.3 | 18.42 | 23.5 | 26.3 | 32.0 |
| 17 | 6.41 | 8.67 | 10.1 | 13.53 | 16.3 | 19.51 | 24.8 | 27.6 | 33.4 |
| 18 | 7.01 | 9.39 | 10.9 | 14.44 | 17.3 | 20.6 | 26.0 | 28.9 | 34.8 |
| 19 | 7.63 | 10.1 | 11.7 | 15.35 | 18.3 | 21.7 | 27.2 | 30.1 | 36.2 |
| 20 | 8.26 | 10.9 | 12.4 | 16.27 | 19.3 | 22.8 | 28.4 | 31.4 | 37.6 |
Список использованной литературы
1. Шрайбер Т.Дж. Моделирование на GPSS. M. Машиностроение. 1980.
2. Руководство пользователя по GPSS World. /перевод с английского/. – Казань: Изд-во «Мастер Лайн», 2002. – 384 стр.
3. Нерсесянц А.А. Моделирование систем и сетей связи. Методическое пособие по дисциплине: «Моделирование систем и сетей связи». Ростов-на-Дону: СКФ МТУСИ, 2013. – 86 с.:








