Вопросы к экзамену по математическому анализу, I семестр.

Дата: 2025-05-01; Просмотры: 2
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

 

1. Множества и действия над ними. Примеры. Натуральные, рациональные, вещественные числа.

2. Понятие функции. Область определения, область значения функции. Обратная функция, сложная функция. График функции.

  1. Основные элементарные функции и их графики.
  2. Понятие предела функции на бесконечности на языке ε-δ. Примеры.
  3. Определения предельной, изолированной, внутренней точки. Открытое и замкнутое множество. Понятие предела функции в точке на языке ε-δ.
  4. Последовательности. Предел последовательности. Сходящиеся и расходящиеся последовательности. Примеры. Определение предела функции в точке на языке последовательностей.
  5. Односторонние пределы. Теорема о единственности предела. Теорема об односторонних пределах.
  6. Замечательные пределы. Вывод первого замечательного предела.
  7. Замечательные пределы. Вывод 3-5 замечательных пределов.
  8. Бесконечно малые и бесконечно большие величины. Порядок малости, эквивалентность. Теорема о замене функции на эквивалентную.
  9. Точки разрыва I и II-го рода. Непрерывность.
  10. Элементарные функции. Их непрерывность. Действия над непрерывными функциями.
  11. Локальные свойства непрерывной в точке функции: ограниченность, сохранение знака.
  12. Теорема Коши. I-ая и II-ая теоремы Вейерштрасса (одна на выбор с доказательством).
  13. Производная функции в точке. Геометрический и физический смысл.
  14. Производная функция. Свойства производных (5 свойств).
  15. Вычисление табличных производных: 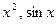. Производная обратной функции.
  16. Дифференцируемая функция. Дифференциал. Геометрический смысл дифференциала.
  17. Приближенные вычисления с помощью дифференциала. Пример. Инвариантность формы 1-го дифференциала. Дифференциалы старших порядков.
  18. Функции, заданные параметрически. Пример. Первая и вторая производная функции, заданной параметрически.
  19. Функции, заданные неявно. Пример. Производная неявной функции. Производные старших порядков.
  20. Возрастание и убывание в точке. Условия возрастания и убывания функции.
  21. Экстремум функции. Теорема Ферма. Геометрический смысл.
  22. Теорема Ролля. Геометрический смысл.
  23. Теорема Лагранжа о конечных приращениях. Геометрический смысл.
  24. Уравнение касательной и нормали к плоской кривой.
  25. Правило Лопиталя. Раскрытие неопределенностей 0/0, ∞/∞, 0∙∞, 1∞, 00, ∞0.
  26. Формула Тейлора для многочлена. Формула Тейлора в произвольной точке. Формула Маклорена. Разложение в ряд Тейлора одной из функций: ex, sin x, cos x, ln(1+x).
  27. Остаточный член формулы Тейлора в форме Пеано и Лагранжа. Разложение в ряд Тейлора одной из функций: ex, sin x, cos x, ln(1+x). Оценка остаточного члена.
  28. Достаточные условия существования экстремума (2 теоремы).
  29. Выпуклость, вогнутость, точки перегиба.
  30. Вертикальные и наклонные асимптоты.
  31. Наибольшее и наименьшее значение. Пример задачи на наибольшее или наименьшее значение.
  32. Понятие кривой в пространстве. Гладкая, регулярная кривая. Уравнение касательной. Касательный вектор. Длина плоской кривой.
  33. Кривизна плоской кривой. Круг кривизны.
  34. Полярные координаты. Примеры кривых, заданных в полярных координатах.