Лекции от 20.03 и от 24.03 – завершающие лекции по теме “Производные”
1)Связь производной с возрастанием и убыванием функции. Локальные экстремумы.
Функция называется возрастающей (убывающей) в точке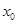 
, если она возрастает (убывает) в некоторой окрестности этой точки (то есть на некотором малом интервале 
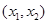, содержащем эту точку).
Утверждение. Если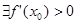 
. то 
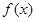возрастает в точке 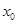. Если 
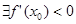. то 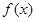убывает в точке .
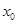Действительно, по формуле Тейлора 1 порядка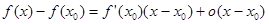 
, откуда следует, что пр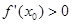и 
и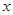 
достаточно близких к 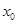приращение функции и приращение аргумента имеют одинаковый знак, то есть функция является возрастающей. Аналогично получается убывание функции при 
.
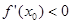Определение. Точка 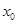называется точкой локального минимума, если для любого 
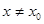из некоторой окрестности этой точки 
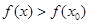. Точка 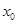называется точкой локального максимума, если для любого 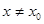из некоторой окрестности этой точки 
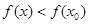. Точка локального минимума или максимума называется точкой локального экстремума.
Утверждение. Если точка 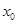является точкой локального экстремума и 
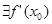, то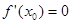 
.
Действительно, в точке локального экстремума функция не является ни убывающей ни возрастающей, поэтому ее производная в этой точке не может быть ни отрицательной ни положительной. Следовательно, остается единственная возможность .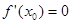
Практически это утверждение можно использовать следующим образом: точки минимума и максимума гладкой функции ищутся среди так называемых стационарных точек, то есть точек, в которых первая производная равна нулю.
Следующие пункты:
2) Теоремы о среднем (Ролля, Коши, Лагранжа);
3) Правило Лопиталя;
4) Формула Тейлора n-го порядка
изложены в пособии “Математический анализ” (файл Мат.ан.2013.pdf), разделы 4.5 - 4.7, стр. 34-38.
5) Связь выпуклости функции и второй производной.
Определение. Функция 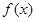называется выпуклой вниз в точке 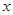, если для всех достаточно малых 
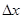выполняется неравенство 
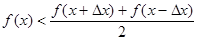(график функции лежит ниже отрезка, соединяющего 2 близкие точки на графике).
Если при этом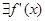 
, то равносильным условием выпуклости вниз является прохождение касательной в точке 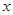ниже графика функции, то есть имеет место неравенство 
.
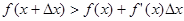Примером функции, которая везде выпукла вниз является парабола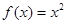 
.
При выполнении противоположных неравенств касательная лежит выше графика функции и функция называется выпуклой вверх в точке 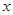(например, парабола 
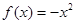везде выпукла вверх).
Определение. Точка, где функция меняет направление выпуклости, называется точкой перегиба.
Утверждение. Пусть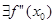 
.
Если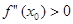 
, то функция выпукла вниз в точке .
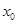Если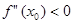 
, то функция выпукла вверх в точке .
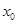Если 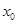- точка перегиба, то 
.
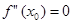Доказательство. По формуле Тейлора 2-го порядка
.
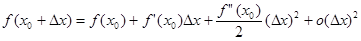Отсюда следует, что при достаточно малых по модулю 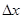и
и 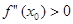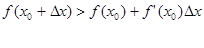функция выпукла вниз в точке .
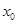Аналогично при достаточно малых по модулю 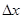и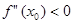
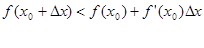и функция выпукла вверх в точке .
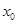Если же 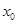- точка перегиба, то функция в этой точке не является выпуклой ни вниз ни вверх, поэтому в этой точке 
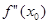не может быть ни отрицательной ни положительной. Следовательно, остается единственная возможность 
.
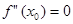Практически это утверждение можно использовать следующим образом: точки перегиба гладкой функции ищутся среди точек, в которых вторая производная равна нулю.