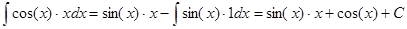Лекция от 07.04. Первообразная и неопределенный интеграл.
Определение. Функция 
называется первообразной для 
, если 
.
Таким образом, операция нахождения первообразной (интегрирования) является обратной к операции нахождения производной (дифференцирования).
Из линейности операции дифференцирования следует, что операция интегрирования также обладает свойством линейности (см. Теорему 6.10 в пособии Мат.ан.2013.pdf, стр. 53).
В отличие от производной первообразная определяется не единственным образом: множество всех первообразных одной функции получается добавлением к одной первообразной произвольной константы С (см. Теорему 6.11 в пособии Мат.ан.2013.pdf, стр. 54).
Определение. Множество всех первоообразных функции 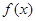называется ее неопределенным интегралом и обозначается 
.
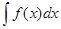Например, при любом вещественном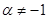 
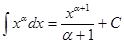
Таблица интегралов для элементарных функций легко получается обращением таблицы производных. Однако, в отличие от дифференцирования, не всякую комбинацию элементарных функций удается проинтегрировать. В некоторых случаях это удается сделать при помощи изложенных ниже приемов.
Основные приемы интегрирования.
Замена переменной
Пусть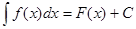 
. Тогда 
.
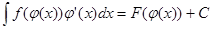Эта формула легко получается путем интегрирования формулы дифференцирования сложной функции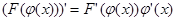 
.
В частности, если внутренняя функция является линейной, то последнюю формулу можно переписать в виде
.
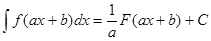Например,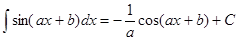 
Интегрирование по частям.
Из формулы дифференцирования произведения следует
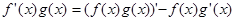
Проинтегрировав обе части этого равенства, получим формулу интегрирования по частям
.
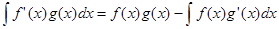Хотя эта формула просто сводит один интеграл к другому, в некоторых случаях она оказывается полезной.
Например, 