Лекция от 02.06. Функции нескольких переменных (ФНП).
ФНП – это функции, область определения которых принадлежит пространству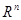 
. ФНП 
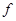каждому элементу 
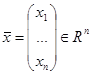ставит в соответствие единственное число 
: 
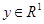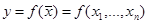. Здесь компоненты вектора 
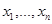называют переменными, от которых зависит функция. Для пространств небольшой размерности их часто обозначают разными буквами.
Если функцию одной переменной геометрически можно представить в виде графика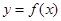 
, то для функций нескольких переменных обычно не удается получить какое-либо графическое представление. Единственный вариант - функция двух переменных: равенство 
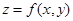определяет поверхность в пространстве. Также кривую на плоскости можно определить в общем случае уравнением вида 
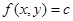, где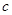 
заданная константа (вспомните уравнения кривых второго порядка). Аналогично поверхность в пространстве можно задать уравнением 
.
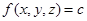Предел ФНП определяется подобно пределу функции одной переменной с заменой в нужных местах абсолютной величины числа на норму вектора (вспомните определение нормы в ).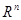
Определение.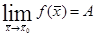 
, если для любого 
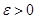существует 
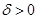, такое что при выполнении неравенства 
( 
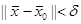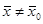) справедливо неравенство 
.
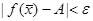Как и в одномерном случае, ФНП называется непрерывной в точке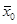 
, если существует 
.
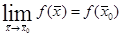Определение. Частной произво
дной функции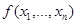 
по переменной 
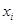называется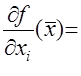 
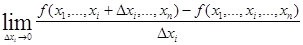. (1)
Из этого определения видно, что частная производная по переменной 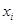вычисляется так же, как обычная производная, если все остальные переменные считать постоянными.
Определение. ФНП называется дифференцируемой в точке 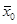, если существует такой вектор 
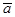, что справедливо представление
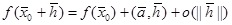при 
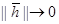(2)
(здесь нужно вспомнить скалярное произведение векторов, определение нормы вектора и символ “o малое”).
Утверждение. Если ФНП дифференцируема в точке 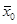, то у нее существуют все частные производные в этой точке, причем 
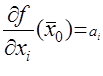(соответствующая компонента вектора ).
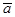Для доказательства этого утверждения достаточно подставить в (2) вектор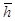 
, у которого i-тая компонента равна 
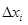, а остальные компоненты равны нулю, выразить из получившегося выражения отношение приращения функции к приращению аргумента и перейти к пределу при 
.
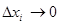Определение. Вектор, состоящий из частных производных ФНП, называется ее градиентом и здесь будет обозначаться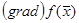 
.
Таким образом, из (2) получается формула Тейлора первого порядка для ФНП:
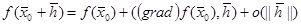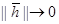при (3)
Известно, что скалярное произведение векторов принимает максимальное значение (при фиксированных нормах векторов), когда векторы идут в одном направлении. Таким образом, из (3) получается геометрический смысл градиента: он показывает в заданной точке пространства переменных направление наиболее быстрого возрастания функции. При этом норма градиента показывает скорость этого возрастания.