Определены все члены функционал ряда.Область сходимости числового ряда это множ-во знач
1)Если каж знач перемнной величины х, принадл некоторому множву Х, соответствует
oдно и только одно знач велич у из множва У, то говорят, что задана ф-я, опред на множве Х со знач в множ У, х назыв аргументом или независ перемнной. Множво Х назыв областью Опред функции, а множво У множвом значений фунции Способы задания: 1.Аналитический(формула),2.Графический (График-множво точ плоскости с координ (х,f(x)) Абсциссы-числа из обл определен,ординаты-соответст знач фуции,3.Табличный,4.Словестный Отношение f, по которому каждому х находящееся соответствие у описывается словесно. Например, y=[x] : x из R (Целой частью х из R называют любое целое число не превосходящее х). Классифф:-алгебраическ(рацион и иррацион(числов и дробные),и трансцендентные (тригонометрич,логарифмич)Если величина y является функцией от u, то есть у = f (u), а u, в свою очередь, функцией от х, то есть u = φ(х), то у является С. ф. от х, то есть y = f [(x)], определённой для тех значений х, для которых значения φ(х) входят в множеств определения функции f (u). В таком случае говорят, что у является С. ф. независимого аргумента х, а u-промежуточным аргументом
2)Чис послед(опред)-если кажд натур числу n Э N постав в соответ Хn Э R,то зад чис посл { Хn} Опред:Число А-предел чис пос {xn},если для любого сколь угод малого полож чис Е найдет такой номер N,что для всех номеров n > N,выполняется нер-во |xn-A|<E.Числ послед, имеющ конечн пред назыв сходящ, в против случ расход. Опред:Пусть фция
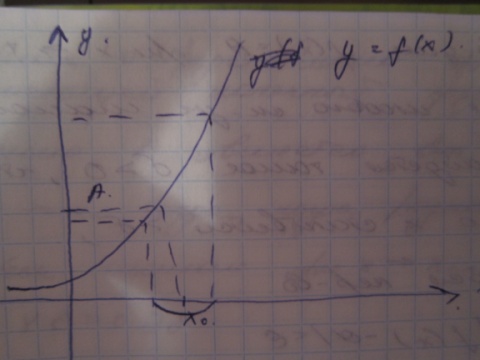
f(x) опред в окрестн х0,кроме точки х0. Число А-пред этой фции при х—х0,если для любого сколь угодно малого Σ>0,найдется δ(дельта)>0,что как только аргумент х удовлетвор нерву 0<|x-x0| <δ,то выпол нерав |f(x)-A|< Σ. И график.
3)Опр:Фунця f(x) бескон малая при х→х0,если ее lim=0 при х→х0.Св-ва:Алгебраич сумма
конечн числа бескон малых фций есть беско малая(это свво вып для конечного числа
б.м. фций, т.е. сумма кон числа б.м. есть б.м.f(х) назыв огран при х→х0 если она огран в нек окрест этой точки.) .Произвед бескон малой фции на огран фцию есть бескон малая.(докво) Следствие: :произвед конеч числа бескон малых явл бескон малой. Об отнош двух б.м. никак общ вывод сдел нел. Опр:Фция f(x) бескон большая при Х→х0,если lim|f(x)|= +∞ при х→х0.Св-ва:Сумма и произвб.б. есть б.б. Произв б.б. на фцию, пред кот=о есть б.б. Отнош б.б. на огран есть б.б. Сумма б.б. и огран.есть б.б. Об
отнош и разнос б.б. общего выв сдел нельз Связь б.б. и б.м.(теорема) велич,обратн б.м. –б.б.и наоб(докво) Связь фции и ее предела: число А это lim(х→х0) f(x) тогда,когда разность f(x)-A-б.м. при х→х0. Сравнение б.м.Пусть α(х) и β(х) –б.м. при х→х0. Если lim(х→х0)α(x)/β(x)=0, то α(х) б.м. более выс порядка, чем β(х). Если этот предел =∞, то β(х) более высокого порядка малости, чем α(х).Если пред равен const, то α(х) и β(х) однопорядк б.м., если пред=1, то α(х) и β(х) эквивал б.м.
4)Теоремы о пред.1)Пред постоянной=постоянной2)Если ф-я имеет кон пред, то он единств(докво) 3)Если фунции f(x) и g(x) име.т кон пред при х→х0, то их сумма, произ, частное тоже имеют кон пред и при этом вып формулы(лист)доква) Пост множ выносит за знак пред(лист)4)Если ф-я f(x) имеет кон пред и в х0 и нек её окрестности сущ корень n-ой степ из f(x), то пред этого корня буд равен корн n-ой степ из f(x) Теоремы о сущ пред:5)Монотонно возраст и огран сверху функция имеет кон предел(то же и с монотонно убыв и огран снизу)6)Теорема о промежуточной ф-ии. Если в нек окрест точки х0 ф-я f(x) заключена между двумя ф-ми g(x) и n(x), кот имеют равн конечн пред, то ф-я f(x) тоже имеет кон пред.(лист) 5)Одност пред:любой интервал (α,х0)назыв лев окрест х0 и наоборот.Если сущ конечн пред ф-ии f(x) при стремлен Х к х0 слева, то этот пред назыв левым пред ф-ии и наоборот(лист) Если для каж ε > 0 сущ такая δ-окрестность точки a, что для всех x, удовл услов |x – a| < δ, x ≠ a, вып нерав |f (x)| > ε,то гов, что ф-я f (x) имеет в точ a беск пред.
6)Замеч пред. 1 зам пред)пред отношен sin бесконеч малой дуги к
самой дуге, выраж в рад=1 :Lim (при α→0) sin α/α=1(докво)(лист)
2 замеч пред) 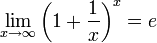
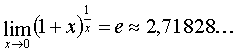
Раскр неопред:(0/0)-разложить на множ числ и знам и сократ члены, стремл к 0
(∞/∞)-разделить числ и знам на х в наивысш степени. Можно применить прав Лоп
(0 -∞) или (∞-∞)- свести к другой неопредел.
7)Фция f(x) непрерывна в т.х0,если есть ее конеч пред при х→х0 и этот пред=знач фции в т.х0 Фция f(x) непрер в т.х0 справа если есть конеч правый пред при х→х0,и этот пред=знач фции в т.х0 и наоборот(слева если есть конечный левый пред).Фция непрер на интервале (а,в) если она непрер в каждой т. этого интервала.Фция непрер на отрезве [а,в],если она просто непрер на интерв (а,в),и в точке а-непрер справа,а в точке в-слева. Необходимое и достат услов непрерыв фции: Для того, чтобы ф-я у = f(х) была непрерыв в х0, необх и дост, чтобы необходимо и достаточно, чтобы пред дельта у, при дельта х стрем к 0, был =0.(лист)
8)Теорема о непре сумм, произв и частн непрерыв ф-ий
Если y=f(x) и y=g(x) непрер в х0, то в этой т непрер ф-ии суммы, произ, частного
этих ф-ий 1). Сумма непрерывных функций есть функция непрерывная.
Доказательство. Пусть фции f(x) и g(x) непрер в точке a. Тогда Lim f(x) при x→a=f(a)
и lim g(x) при х→а = g(a).Согласно свойству пределов фций сущест пределов фций f(x)
и g(x) гарантирует существование предела их суммы. При этом
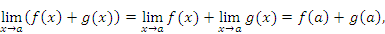 что и требовалось доказать.
что и требовалось доказать.
Докво теорем 2 и 3 аналогично,только сумму мен на произв и частное.
Непрерывность сложной функции: Пусть y=f(x) опред на числ промке U, а y=u(x) опред на Х, тогда, если ф-я u=f(x) непрерыв в т х0, а ф-я y=f(x) непрер в соотв т u0=f(x0), то сложн ф-я y=f(u(x)) непрер в х0.Док-во: Зададим произвольное Σ > 0.Так как f(t) непрерывна в точке b, то γ > 0 такое что, | f(t) - f(b) | < Σ при | t - b | < γ.Отсюда следует, что| f(ϕ (x)) - f(ϕ (a)) | < Σ при | ϕ (x) - ϕ (a) | < γ. (1) Так как ϕ (x) непрерывна в точке a,то для указанного γ существует δ > 0 такое что | ϕ (x) - ϕ (a) | < γ при | x - a | < δ.(2) Из (1) и (2) следует, что | f(ϕ (x)) - f(ϕ (a)) | < Σ, если | x - a | < δ, что и требовалось доказать.
9)Св-ва непрерывных фций:1.Теорема Вейерштрасса: Если функция опред и непрер на отрезке [а, в] , то она ограничена и достигает своего наим. и наиб. Значения на этом отрезке. 2.Теорема Больцано-Коши: Если функция опред. и непрер. на отрезке [а, в] и на его концах принимает значения противоположных знаков, то на интервале (а, в) найдется хоть одна точка С, в которой функция будет = 0. 3.Теорема(3): Если функция опред. и непрер. на [а, в] ,а m и M- наим. и наиб. значения на этом отрезке, то для любой точки С из отрезка [m, M] найдется хотя бы одна точка Сна отрезке [а, в] такая, что
выполняется равенство:f(c)=C Классификац точек разрыва:если в нек. Точке нарушено усл непрерыв, то такую т. назыв Т. разрыва .Опред: если есть конеч односторон пред фции y=f(x) в т.х0 и хотя бы 1 их них не = знач фции в т.х0,то х0 –это точка разрыва 1 р., а величина(дельта)(лист) назыв скачком ф-ии(разность одност пред) Если в т. разрыва 1 р.одностпред равны, то разрыв назыв устран. Если сущ кон прав пред в х0 и он =знач ф-ии в х0, но лев не равен, то в х0 справа непрер-ть, слева-разрыв. Опред:если хотя бы 1 из односторонн lim f(x) в т.х0не существует или обращается в беконечность то х0-это разрыв 2 рода.
10)Пред положен М0М1 при стремлен М1кМо вдоль кривой назыв касательной ф-ии в точке с абсциссой М0(лист)
11)Опред: Производ фции y=f(x) в точке х назыв пред отнош приращ фции к приращ аргумента при стремл послед к 0, если этот пред сущ и конечен(лист) Геометр смысл: tg угла наклона касательной,пров к граф фции в т.х0 = значен произв фции в этой точке: f ’(x0)=k=tg ϕ/ Физич.смысл: скорость движ т. в момент времени= произв пути во времени.Ур-ние касат к граф ф-ии y=f(x0) в точке (х0;у0) имеет вид у-у0=f’((х0)(х-х0) 12)Опр.Если пред(∆x→0)∆y/∆x=±∞,то полагают что произв обращается в беск.Если есть кон пред(∆x→0+0)∆y/∆x,то его назыв левосторонней
произв ф-ии: f ’+(x) .Если есть конеч (∆x→0-0)∆y/∆x,то его назыв правосторон
произв фции: f ’_(x).Опред:фция y=f(x) назыв диф в т.х,если она
имеет в этой точке конечн производн,и назыв недиффер,если произв в точке
не существует или обращается в беск.
13) Т: если ф-я у= f(x) диф в т.х,то она в этой точке непрер.
Док-во: пусть фция у= f(x) деффер в т.х,значит есть и произодн у=lim(∆x→0)∆y/∆x
∆y/∆x=y ’ + α(∆x), lim ∆ y = lim (∆ x → 0)( y ’∆ x +α(∆ x )∆ x )-приращ диффер фции.
lim ∆ y = lim (∆ x → 0)( y ’∆ x +α(∆ x )∆ x )= lim (∆ x → 0) y ’ ∆ x + lim (∆ x → 0) ( |α|∆ x )∆ x ))=0+0
значит ф-я непрер в точке х.Следствие:если фция в точке разрыва,то она не
диф в этой точке и не имеет конеч производн.Обрат не вып,то
есть ф-я м. б. непрер,но диффер-мой не явл.(докво)
14)Теорема:если ф-я u(x) и v(x) диф в т.х,то: 1) алгеб сумма этих
ф-й тоже диф в т.х и выполняется рав-во: (u+v) ’=u ’+ v ’
2)произв этих ф-й тоже диф: (uv) ’=u ’v + uv ’
3)частное этих ф-й тоже диф:(u/v) ’=(u ’ v – uv ’)/v2, но v не = 0
15)Опр:производ фции f(x) назыв lim отношения приращения фции к приращ
независимой переменной при стремлении последнего к 0 (если этот lim есть)
Таблица произ: x ’=1; c’=0; (uα) ’=αuα-1 ;( √x) ’=x ’/2√x ; (1/x) ’= -x ’/x 2;
(ax)’=axlnau ’;(eu) ’=euu ’; (logau) ’=u ’/lnau’; (lnu) ’=u’/u ; (sinu) ’=
=cosuu’ ; (cosu) ’= -sinuu’ ; (tgu) ’=u ’/cos2u ; (ctg) ’= -u’/sin2u ;
(arcsinu) ’=u’/√1-u2 ; (arcos) ’= - u’/√1-u2; (arctgu) ’= u’/1+u2;
(arcctg) ’= - u’/1+u2.Теорема о произв слож ф-ии: Если фция u=ϕ(x) имеет
произ ux’ в точке x, а функция y=f(u) имеет производную yu ’ в соответст точке u=ϕ(x),
то сложная фция y=f(ϕ(x)) имеет произв yx’ в точке x, которая находится по формуле
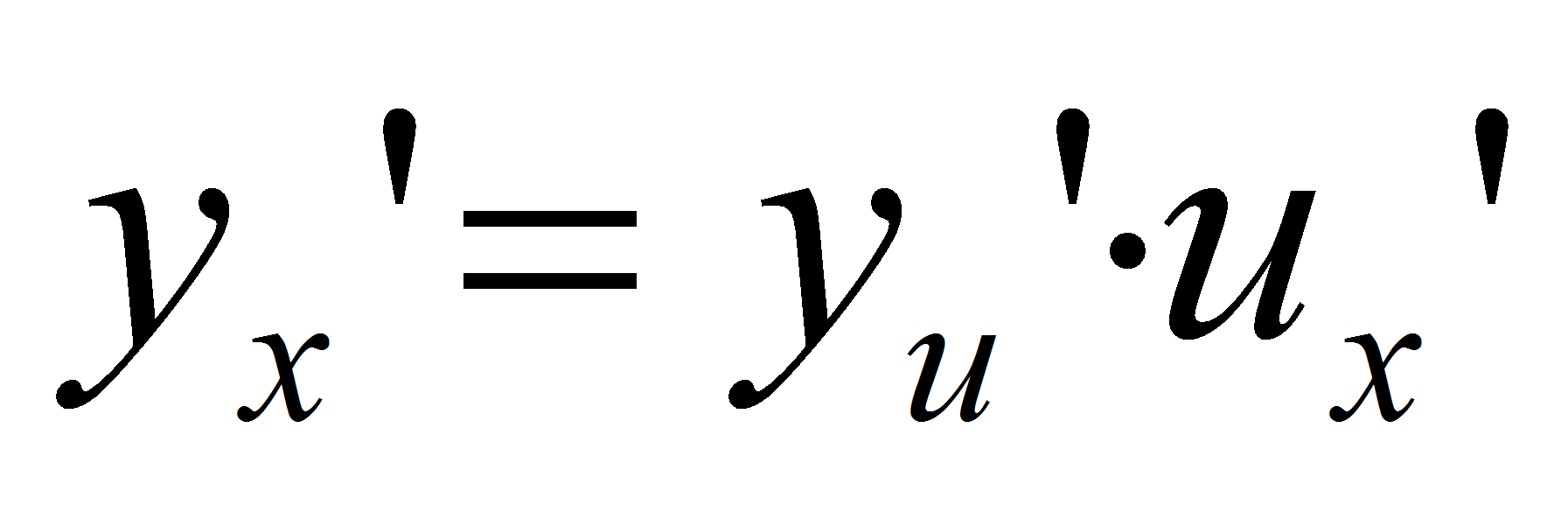 .Док-во:По условию
.Док-во:По условию 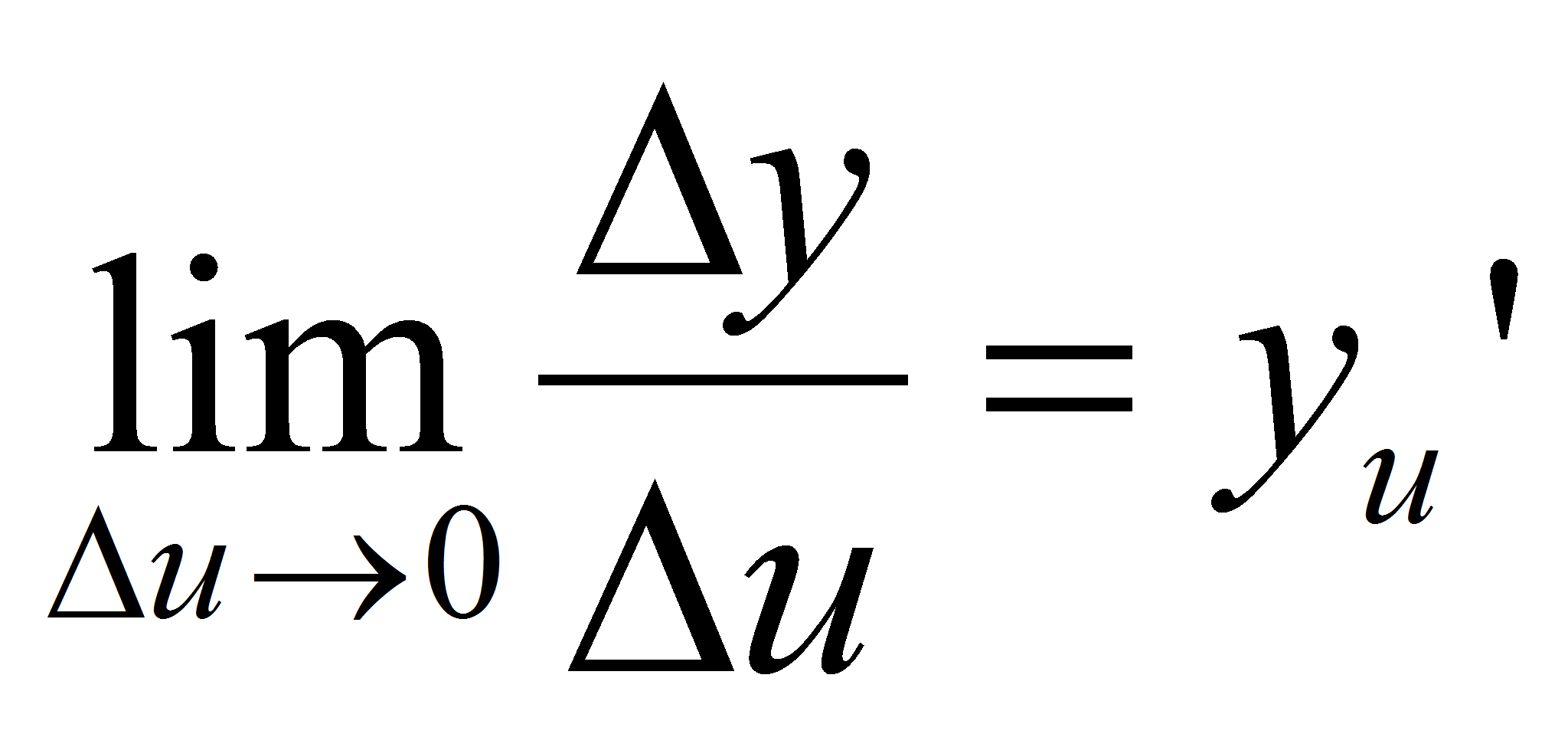 . Отсюда, по теореме о связи
. Отсюда, по теореме о связи
фции, её предела и бесконечно малой фции, имеем 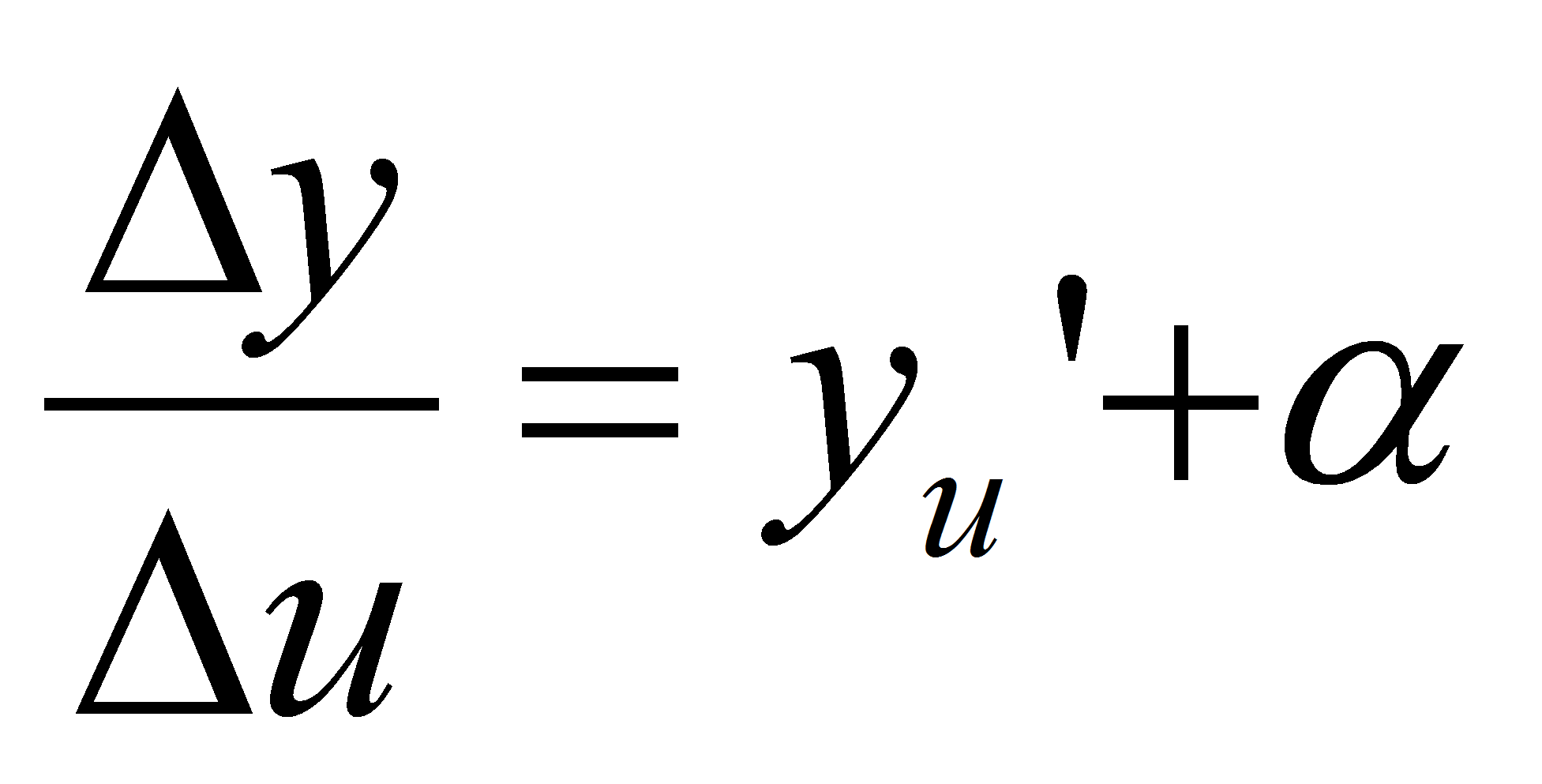 или
или
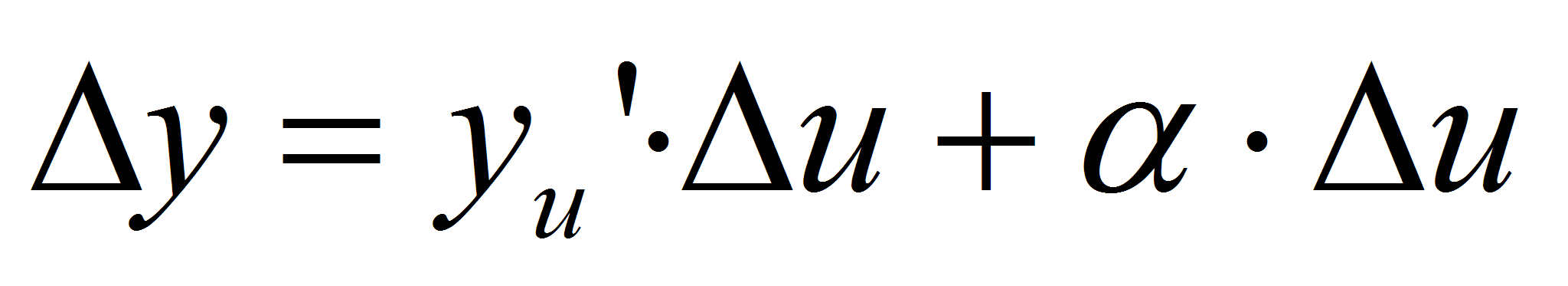 , где a→0 при ∆u→0.Функция u=ϕ(x) имеет производ в
, где a→0 при ∆u→0.Функция u=ϕ(x) имеет производ в
точке x: 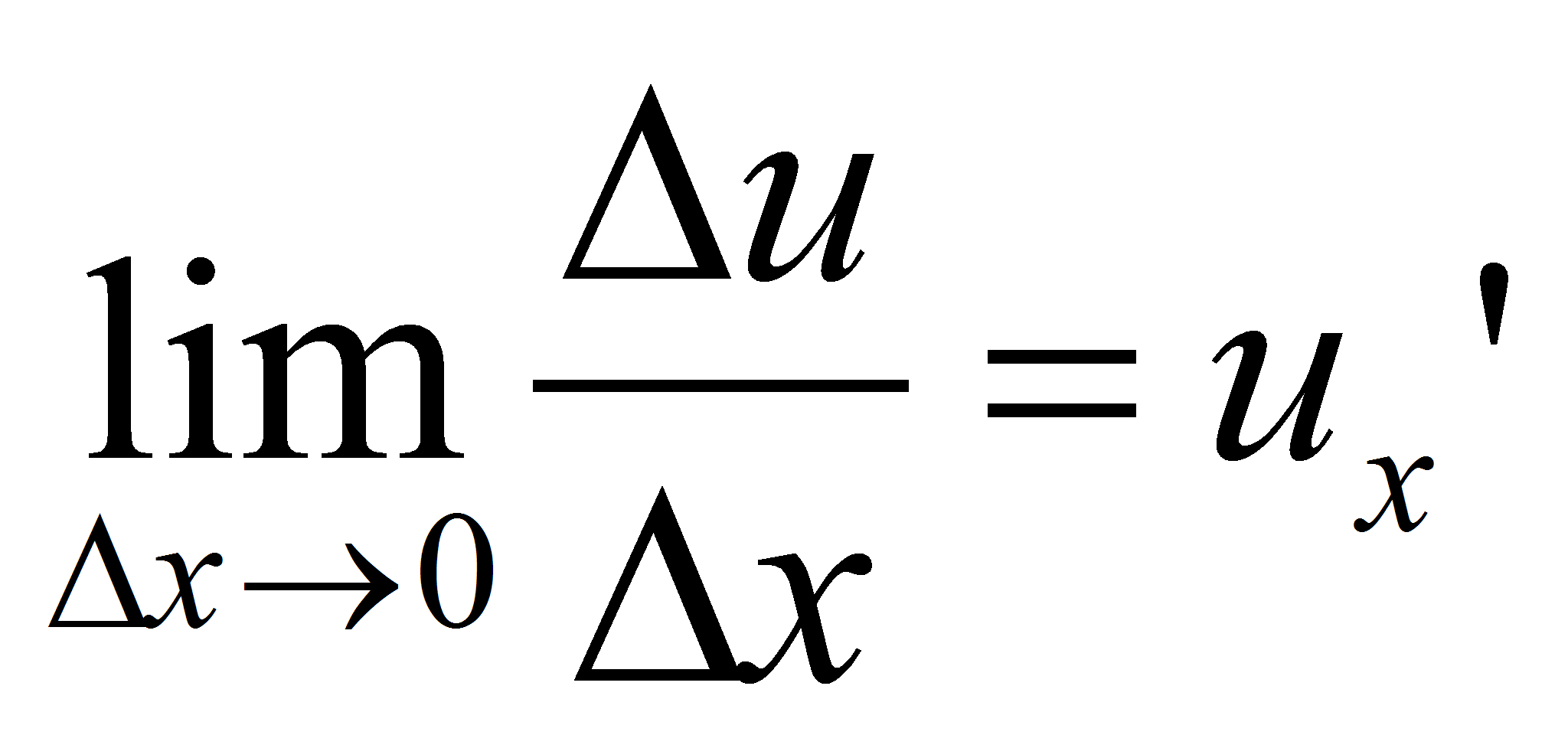 , поэтому:
, поэтому: 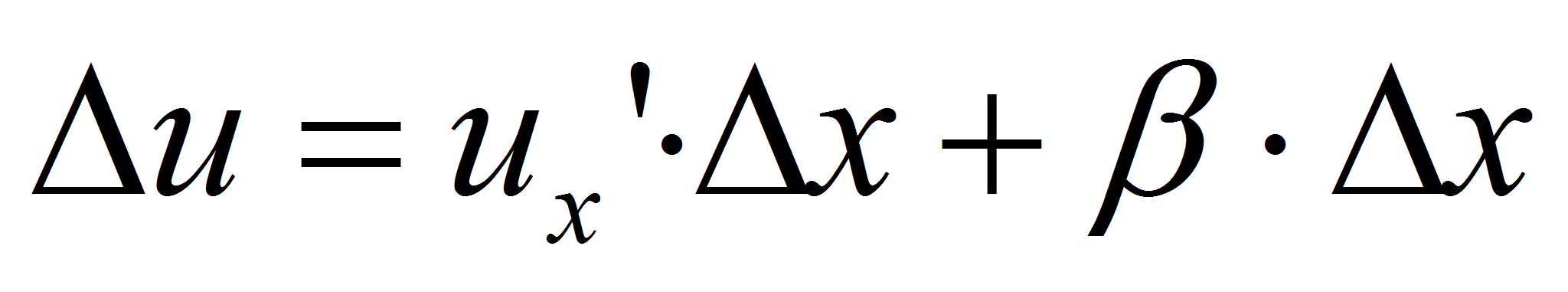 , где β→0 при ∆x→0.
, где β→0 при ∆x→0.
Подставив значение ∆u в равенство 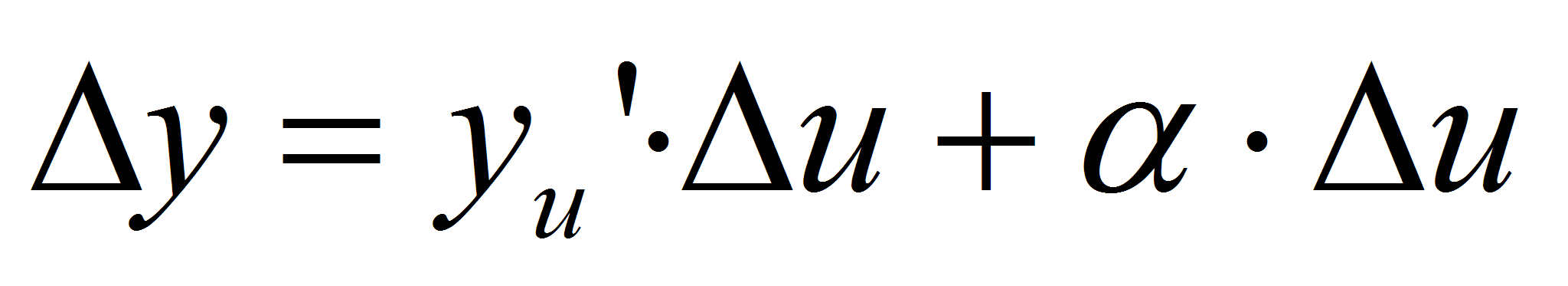 , получим:
, получим:
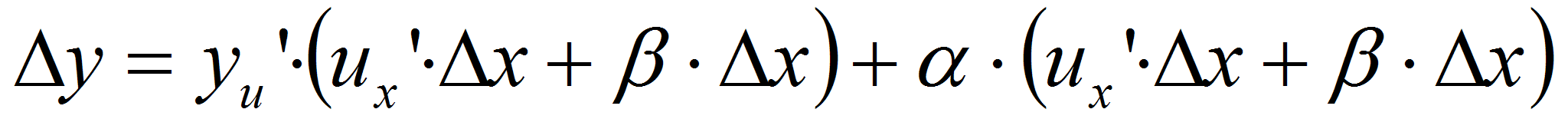 ;
;
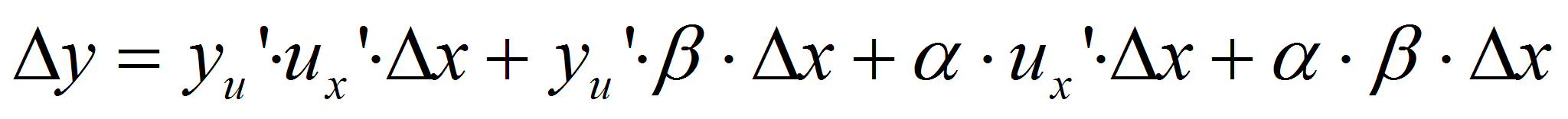 . Разделим получ равен
. Разделим получ равен
на ∆x и перейдя к пределу при ∆x→0, получим 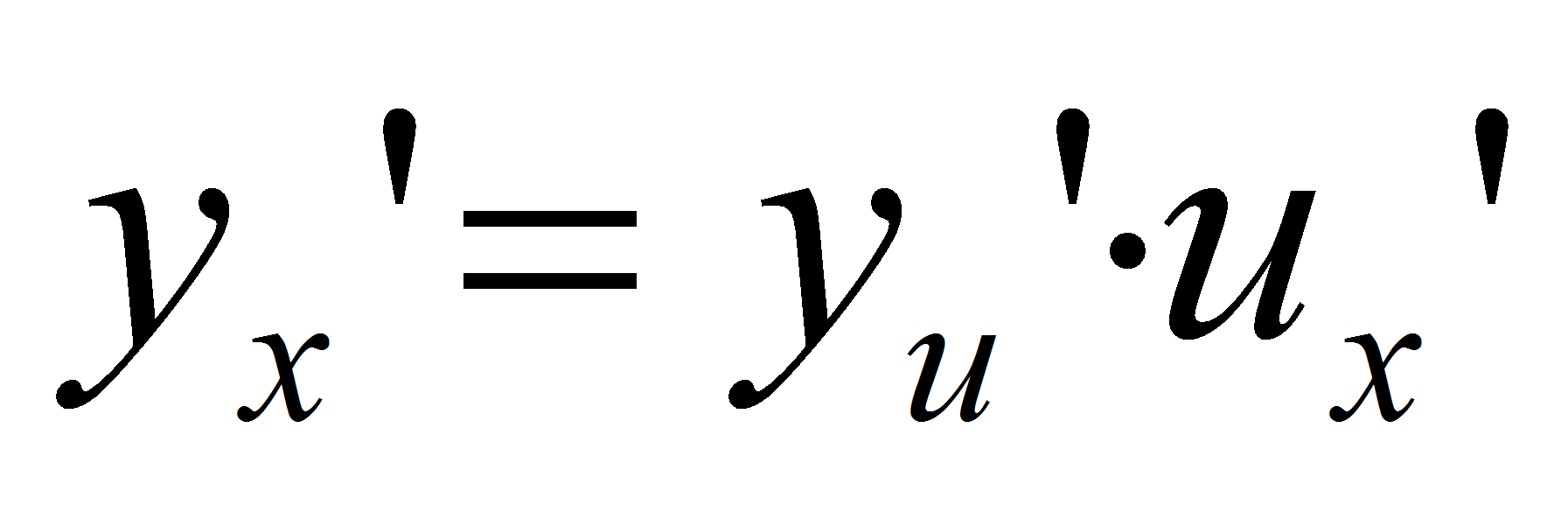 .(лист)
.(лист)
16)Опр: линейн, относ ∆х часть приращ ф-ии назыв диф ф-ии(dy) и =f’(x)
Св-ва дифф:1)Дифф-ал постоянной равен нулю:dc = 0, с = const.2)Дифф-ал суммы
диф ф-й равен сумме дифф-лов слагаемых: d(u+v)=du + dv.Следствие:если две диф ф-и
отлич постоян слагаемым, то их дифф-алы равны: d(u+c) = du (c= const).3)Диф произв
двух дифф-мых фций равен произведению первой фции на дифф-ал второй плюс
произведение второй на дифф-ал первой:d(uv) = udv + vdu.Следствие. Постоянный
множит можно выносить за знак диф-ала: d(cu) = cdu (с = const).4)Диф-иал частного u/v
двух диф-мых фций и = и(х) и v = v(x) определяется формулой d(u/v)=(vdu – udv)/ v 2
Геометр смысл диф-ла: проведем к граф ф-и y=f(x) в точку M(x,y) касат MT и рассмот
ординату этой касат для точки x+∆x. На рис |AM|=∆x, |AM1|=∆y. Из прямоуг треуг MAB
имеем: tgα=|AB|/∆x, т.е.|AB|=∆xtgα . Но, согласно геометр смыслу производ, tgα=f ’(x).
Поэтому AB=f ’(x)∆x или dy=AB. Это означает,что диф-ал фции y=f(x) в т.х равен приращению
ординаты касат к граф фции в этой точке,когда x получает приращение ∆x. Инвариантность: Пусть теперь дана сложная (дифференцируемая) функция , где 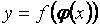 Тогда по формуле производной сложной функции находим
Тогда по формуле производной сложной функции находим 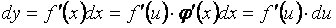 ,так как
,так как 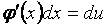
Итак 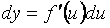 , т.е. формула дифференциала имеет один и тот же вид для независимой переменной и для промежуточного аргумента,представляющего собой дифференцируемую функцию от х.
, т.е. формула дифференциала имеет один и тот же вид для независимой переменной и для промежуточного аргумента,представляющего собой дифференцируемую функцию от х.
Произ высших порядков:Пусть y=f(x) нек диф ф-я, произ от кот тоже диф. Произв ф-ии
у '(х)= f '(x) обознач y''= f''(x) и назыв 2-ой произ или произ высш порядка.
17) При вычислении пред для раскрытия неопределенностей вида (0/0) и (∞/∞)
используется теорема, известная как правило Лопиталя.Теорема:Пред отношен
двух б.м и б.б. ф-й равен пред отношения их производных, если последний существует.
Примечания:1)Эта теорема справедлива при x→ ± ∞ .2)Правило Лопиталя можно
применять повторно.3)Применяя правило Лопиталя, надо дифференцировать не дробь,
а отдельно числитель и знаменатель.4)На каждом этапе применения правила Лопиталя
следует пользоваться упрощающими отношение тождественными преобразованиями, а
также комбинировать эти правила с любыми другими приемами вычисления пределов.
18) 1. Условие постоянства функции.Теорема. Пусть функция f(x) определена в промежутке X и имеет внутри него конечную производную f ’(x),а на концах (если они принадлежат X) сохраняет непрерывность. Для того чтобы f(x) была в X постоянной, достаточно условие f ’(x)=0 внутри X. Доказательство. Пусть это условие выполнено. Фиксируем некоторую точку x0 из промежутка X и возьмем любую другую его точку x. Для промежутка [x0, x] [x, x0] удовлетвор все условия теоремы Лагранжа(если функция f (x) непрерывна на отрезке [a; b] и диф-ема на интервале (a; b), то существует хотя бы одна точка x0 Э (а,б) такая, что f(b)-f(a)=f ’(x0)(b-a))
След можем написать f(x) – f(x0)=f¢(c)(x - x0), где c содержится между x и x0, а значит,
заведомо лежит внутри X. Но, по предпол-ю, f(c)=0, так что для всех x из X
f(x)=f(x0)=const,и наше утверждение доказано.
19) Опред: ф-я у=f(x) возраст на числ пром-ке Х, если для люб двух точек х1,х2 из того, что х1меньше Х2 след f(x1) меньш f(x2)(больш знач аргум соответ больш знач ф-и)убывающ-наоборот Необ и дост усл возраст и убыв ф-ии.1)Если диф-емая ф-я y=f(x) возрастает на [a, b], то ее произв неотрицательна на этом отрезке, f '(x)≥ 0 и наоборот.2)Обратно. Если ф-я y=f(x) непрерывна на [a, b], дифф-ма на (a, b) и ее произ-ная положительна этом отрезке,f ' (x)≥ 0 для a<x<b, то f(x) возрастает на[a, b]. Док-во:
1)Докажем первую часть теоремы. Итак,пусть ф-я y=f(x) возрастает на [a, b]. Зафиксируем на этом отрезке произвольную точку x, придадим ей приращение Δx. Тогда если Δx>0, то x<x+Δx. Поэтому по определению возрастающей функции f(x)<f(x+Δx), то есть f(x+Δx) - f(x)>0. Но тогда и (f(x+∆x)-f(x))/∆x>0. Аналогично, если Δx<0, то x>x+Δx и значит f(x+Δx)-f(x)<0,а (f(x+∆x)-f(x)) /∆x>0 . Переходя в этом равенстве к пределу при Δx→0, получим lim(∆x→0) (f(x+∆x)-f(x))/∆x≥0 ,
то есть f '(x)≥0.2)Докажем вторую часть теоремы. Пусть f '(x)>0 при всех x Э (a,b). Рассмотр 2 любых значения x1 и x2 таких, что x1 < x2. Нужно док-ть,что f(x1)< f(x2). По теореме Лагранжа существует такое число c Э (x1, x2), что f(x2)-f(x1)=f ’(c)(x2-x1). По условию f '(x)>0, x1 – x2>0Þ f(x2)-f(x1)>0, а это и значит, что f(x) – возраст ф-я.
2. Если f(x) убывает на[a,b], то f ’ (x)< либо = 0 на этом отрезке. Если f ’ (x)<0 на (a; b),
то f(x) убывает на [a, b],в предположении ,что f(x) непрерывна на [a, b]. Возрастание и убывание функции характеризуется знаком ее произв. Чтобы найти на каком промежутке ф-я возраст или убывает, нужно определить, где произв этой ф-и только положит или только отрицат,то есть решить нерав-ва f '(x)>0 – для возраст или f '(x)<0 – для убыв.
20) Опред: Пусть фция y=f(x) определена на (а,в).Точка х0 Э (а,в) назыв. точкой
макс(мин),если найдется некотор окрестность этой точки, для всех точек кот
будет выполняться условие: f(x)<f(x0) (f(x)>f(x0). Точ макс(ми)-это точки экстремума.Теор:Необ признак эксрем:если т.х0-это т. макс (мин),
то произв в этой т. =0 или не сущ.(докво)Необ усл экстр дост не явл. Внутр точки из обл опред котор произв или не сущ, или =0, или = беск, назыв крит точками. Это точки возм экстрем. Точки произв кот=0 назыв стацион. Теорема: Достат призн экстрем: 1)Пусть xо - критич точка. Если f ' (x) при переходе через точку xо меняет знак плюс на минус, то в т. xо ф-я имеет макс,в прот случае - мин. Если при переходе через критич точ произв не меняет знак, то в точке xо экс нет.2)Пусть функция f(x) имеет произв f ' (x) в окрест т. xо и вторую произ-ную f"(xo) в самой точ xо. Если f '(xо) = 0, f"(xo)>0 (f"(xo)<0), то точка xо является точкой мин (макс) ф-и f(x). Если же f"(xo)=0, то нужно либо пользоваться первым достаточным условием либо привлекать высшие производные.
21)Опр:граф ф-и y=f(x) назыв вып (вогнут) на (а,в),если касат к граф,провед
в любой т. этого интервала,распол над (под) граф ф-и.Теорема: если 2 произ-ная
дважды дифф-мой фции на некотором интервале положительна(отрицат),то
граф ф-и на этом интервале вогнут(вып)Точки, в кот происх направл вып(вогнут),
назыв точки перегиба.
22)Теорема.1)Достат усл вып вниз: если ф-я у=f(x) имеет на числ пром-ке Х
полож вторую произв, то граф ф-и будет вып вниз на этом пром-ке(докво)
дост усл вып вверх: если ф-я у=f(x) имеет на Х отриц втор произв, то граф буд
вып вверх на всем пром-ке.
23) Теорема: Необх усл перегиба: Если т.х0-это т.перегиба граф
дважды диф ф-и,то в это точке 2-ая произв =0. Опр:точки,в котор
2-ая произ-ная =0, или не сущ, или =+-беск назыв критические точки.Достаточ
услов перегиба:если 2-ая произ-ная,дважды диффер в нек точке ф-и =0 и при
переходе через нее 2-ая произв мен знак,то данная точка-это точка перегиба.
24)Опр: прямая х=а назыв вертик асимптотой к граф ф-и y=f(x),если хотя
бы 1 из односторон пределов обращен в беск: lim(х→а ±0) f(x)
= +∞ или - ∞,а в точке а ф-я терпит разрыв 2 рода. Опр:прямая у=в назыв
горизонт асимптотой к граф ф-и у=f(х) если lim(x→± ∞)f(x)=в.Опр:прямая
у=kx+b назыв наклонной асимптотой к граф фции,если ф-ю можно
представить в виде f(x)=kx+b+α(x),где α(х)-бесконеч малое при х→∞
25)Опр: фция F(x) назыв первообразной для ф-и f(x) на пром-ке х, если в каж
точке х этого пром-ка F ’(x)=f(x).Опр:совокупность всех первообраз для ф-и f(x)
на пром-ке Х назыв неопред инт от ф-и f(x) и обознач ∫ f(x)dx. Теоремы: 1)если F(x)
это первообр f(x) то любая ф-я вида F(x)+с тоже первообр для f(x) 2) если F1(x) и F2(x)
первообр для f(x) тогда их разность это нек const Св-ва неопр интег:1)произ-ная от неопр
интег равна подынтегр ф-и ( ∫f(x)dx) ’=f(x).2)диффер-циал от неопр интег равен подынтегр выр-ю d( ∫f(x)dx)=f(x)dx.3)неопр интегр от диф-ла некотор ф-и равен этой ф-и плюс константа ∫ dF(x)=F(x)+c. 4)постоян множит вын за знак неопр интег∫ kf(x)dx=k ∫ f(x)dx. 5)неопред интегр от алгебраич суммы нескольких ф-й равен алгебраич сумме неопред интегр этих ф-й.∫(f1(x)±f2(x))= ∫f1(x)±∫f2(x). Независим вида неопр интегр от выбора аргум:всяк формула интег-ния сохраняет свой вид при подстановке вместо независим переменной любой диф-мой ф-и, т.е.если ∫ f(x)dx=F(x)+C где F ’(x)=f(x)
то ∫ f(u)du=F(u)+C где u=u(x) – любая диф-мая ф-я.Пример:если ∫sinxdx= -cosx+C, то∫ sinudu= -cosu+C, где –ф-я от х.Таблица неопр интег:∫0dx=c; ∫dx=x+c; ∫xαdx=(xα+1/α+1)+c;
∫dx/x=ln|x|+c;∫sinxdx= -cosx+c;∫cosxdx=sinx+c;∫exdx=ex+c;
∫axdx=ax/lna +c;∫dx/√1-x2=arcsinx+c;∫dx/1+x2=arctgx+c;∫dx/cosx2x=
=tgx+c; ∫dx/sin2x= -ctgx+c;∫dx/a2+x2=1/a ∙arctgx/a+c;∫dx/√a2-x2=
=arcsinx/a+c; ∫dx/x2-a2=1/2a∙ln|x-a/x+a|+c; ∫dx/√x2+a=ln|√x2+a|+c
Непосредств интегрир:это интегрир с помощью свойств интегралов и таблицы.
26)Метод замены перемен:Рассмот неопред интег F(x) некоторой ф-и f(x).
Для упрощения вычисления интег часто удобно выполнить замену перемен.
Переход от x к новой перемен u описывается выражением
∫f(x)dx=∫f(g(u))g’(u)du=F(u)=F(g-1(x)). где x = g (u) - подстановка.Соответственно,
обратная -ия u = g −1(x) описывает зависимость новой переменной от старой.
Пример:Вычислить 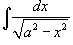 Сделаем замену u=x/a . Тогда x=au, dx=adu
Сделаем замену u=x/a . Тогда x=au, dx=adu
.Следовательно, интеграл принимает вид
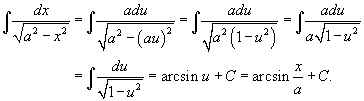
Метод интегрир по частям: пусть u=u(x) и v=v(x)-это диф-е фи.По св-ву диф-ала:D(uv)=vdu+udv. Интегрируя правую и левую части получим:∫udv=uv+∫vdu.Это формула Интегрир по частям.При ее применении фиксируется разбиение подынтегрального выр-я искомого интегр на 2 сомножителя (u и dv).При переходе к правой части 1 из них диф-ется(du=u ’dx),а второй интегрируется (v=∫dv+c).
27)Задача о вычислении Sкрив трапец(фигура на плоск, образ отрез (а:b), верт прям А и Б и граф Непрерын неотрц ф-и у=f(x) назыв кривол трап) Пусть на [a,b] есть неотрицат,
Непрерыв ф-я y=f(x) аАВb-это криволинейн трапец1)произвольно разбиваем отрезок [a,b] по оси ОХ на n-частных отрезков,точки обозначаем а=х0<х1<…<xi<xi+1<..xn=b.В каждом частич отрезке [xi-1;xi] нах знач ф-и f(x) в точке ξi f(ξi).Обозначим разность ∆хi=xi-xi-1 x через ∆х Обознач длину наибольш част отрезка ∆х=max∆xi Находим сумму произведений значений ф-и f(ξi) на ∆хi ,это будет G= f(ξi)-∆xi .G-интегральная сумма ф-и f(x) на отрезке [a,b].Находим предел G при ∆х→0.Площадь трапеции=lim(∆x→0)G=
=lim(∆x→0)Σni=1f(ξi)∆xi. Опр:если есть конеч предел итегральной Суммы G при ∆х→0,не зависящий от способа разбиения [a,b] на частичные отрезки и выбора точек
ξi то этот предел называется опред интегралом f(x) на [a,b]. lim(∆x→0)Σni=1f(ξi)∆xi.=
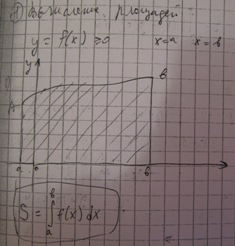
= 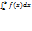 . Геометрич смысл опред интегр: Если f(x) непрерывна и положительна
. Геометрич смысл опред интегр: Если f(x) непрерывна и положительна
на [a, b], то интеграл 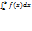 представляет собой площадь кривол трап,
представляет собой площадь кривол трап,
огран линиями y = 0, x = a, x = b, y = f(x).Св-ва опред интегр:1) опред интег-это число,
зависящее от промежутка интегрир [a,b],подинтеграл фции f(x) и независящ от переменной интегриров 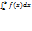 =
= 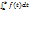 . 2)если а=b,то
. 2)если а=b,то 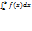 =
= 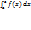 =0
=0
3)при перемене мест пределов ин-я интегр лишь мен свой знак.4) при любом располож точек a,b,c в пром-ке интегрируемости f(x) выполняется рав-во: 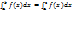 +
+ 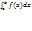 .5)постоянный множ выносится за знак опред интегр6)опред интерг от алгебраич суммы нескольких ф-й равен алгебр сумме опред интегр этих ф-й. 7)если на [a,b] f(x)
.5)постоянный множ выносится за знак опред интегр6)опред интерг от алгебраич суммы нескольких ф-й равен алгебр сумме опред интегр этих ф-й. 7)если на [a,b] f(x)  g(x), то
g(x), то 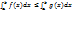 .Теорема о среднем знач: если f(x) непрерывна на [a,b] то на этом отрезке найдется такая точка С,что
.Теорема о среднем знач: если f(x) непрерывна на [a,b] то на этом отрезке найдется такая точка С,что 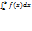 =(b-a)f(c ).Док-во: f(x) непрерыв на [a,b],значит есть m-наименьш знач И W-наибольш знач. m<F(x)
=(b-a)f(c ).Док-во: f(x) непрерыв на [a,b],значит есть m-наименьш знач И W-наибольш знач. m<F(x)  W проинтегрир нер-во m(b-a)
W проинтегрир нер-во m(b-a) 
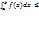 W(b-a)/:(b-a) m
W(b-a)/:(b-a) m 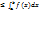 /(b-a)
/(b-a)  W. c э [a,b]. f(c )=
W. c э [a,b]. f(c )= 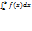 /(b-a)
/(b-a)
f(c)(b-a)= 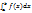 . Теорема (существ первообраз для непрер фции):Если
. Теорема (существ первообраз для непрер фции):Если
f(x) непрер на [a,b],то Ф(х)= 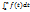 диффер-ема на [a,b] и ее пр-ная
диффер-ема на [a,b] и ее пр-ная
Ф ’(х)=f(x).Док-во:возьмем х э [a,b],даем приращ ∆х,попадаем в точку х+∆х э [a,b],
Тогда Ф получит приращ ∆Ф=Ф(х+∆х)-Ф(х)= 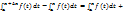
+ 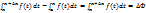 ξ э [x,x+∆x] рассмотрим ∆Ф/∆x=
ξ э [x,x+∆x] рассмотрим ∆Ф/∆x=
= 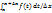 = ∆xf(ξ) / ∆x= f( ξ) ; lim(∆x→o)∆Ф/∆x= lim(∆x→o)f(ξ)=f(x) Ф ’(х)=f(x)
= ∆xf(ξ) / ∆x= f( ξ) ; lim(∆x→o)∆Ф/∆x= lim(∆x→o)f(ξ)=f(x) Ф ’(х)=f(x)
28)Вычисление опред интегр:1)через замену перемен:пусть ф-я ϕ(t) имеет непрер производ на отрезке (α,β), а=ϕ(α), b=ϕ(β) и ф-я f(x) непрерыв в каждой точке х вида х=ϕ(t),где t э [α,β]. Тогда справедливо рав-во: 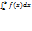 =
= 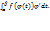 2) Интегрир по частям: пусть ф-и U=u(x) и v=v(x) имеют непрерыв произв на [a,b],тогда:
2) Интегрир по частям: пусть ф-и U=u(x) и v=v(x) имеют непрерыв произв на [a,b],тогда:  ab -
ab - 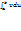 где
где  ab=u(b)v(b)-u(a)v(a).3)непосредствен интегрирован.формула
ab=u(b)v(b)-u(a)v(a).3)непосредствен интегрирован.формула
Ньютона-Лейбница:Если f(x) непрер на [a,b], а F(x)-первообраз ф-и f(x),то
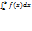 =F(b)-F(a)=F(x)|ba. Док-во: Ф(х)=
=F(b)-F(a)=F(x)|ba. Док-во: Ф(х)= 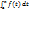 -это Первообраз для f(x). Ф(х)=F(x)+c , x=a, Ф(а)=F(a)+c; c= -F(a) ; Ф(а)=
-это Первообраз для f(x). Ф(х)=F(x)+c , x=a, Ф(а)=F(a)+c; c= -F(a) ; Ф(а)= 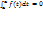 ; Ф(х)=F(x)-F(a); X=b; Ф(b)=F(b)-F(a); Ф(b)=
; Ф(х)=F(x)-F(a); X=b; Ф(b)=F(b)-F(a); Ф(b)= 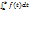 ;
; 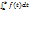 =F(b)-F(a).
=F(b)-F(a).
29)Несобст интегр 1 рода:1) пусть f(x) непрер на [a,+∞). 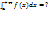
Рассмотрим 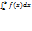 = F(b)-F(a); F(x)-первообраз f(x); lim(b→+∞)f(x)dx=lim(b→+∞)(F(b)-F(a)) (1) Опр: если есть конеч предел (1),то говорят что несобств интегр
= F(b)-F(a); F(x)-первообраз f(x); lim(b→+∞)f(x)dx=lim(b→+∞)(F(b)-F(a)) (1) Опр: если есть конеч предел (1),то говорят что несобств интегр 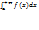 сходится И равен этому пределу.Вобратном случае он расходится,т.е. он равен ∞ или не существует. 2) пусть f(x) непрер на ( -∞;в].
сходится И равен этому пределу.Вобратном случае он расходится,т.е. он равен ∞ или не существует. 2) пусть f(x) непрер на ( -∞;в]. 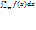 -? Выбираем а <в. Рассмотрим
-? Выбираем а <в. Рассмотрим 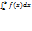 = F(в)-F(a) lim(a→ - ∞)
= F(в)-F(a) lim(a→ - ∞) 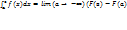 ) (2). Опр: если есть конеч предел
) (2). Опр: если есть конеч предел
(2),то несобствен интегр 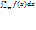 сход и =этому пред. И расходится если
сход и =этому пред. И расходится если
пред не сущ или =  .Интегр Пуассона:
.Интегр Пуассона: 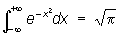 .Несобс интег 2
.Несобс интег 2
Рода( от разрывных ф-й) 3) пусть f(x) непрер на [a,b). Возьмем Е>0.Рассмот 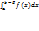 =
=
=F(b-E)-F(a); lim(E→0+0) 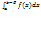 =); lim(E→0+0)( F(b-E)-F(a)) (3). Опр:если есть
=); lim(E→0+0)( F(b-E)-F(a)) (3). Опр:если есть
кон пред (3) то несобств интегр 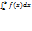 назыв сходящ и равен ему. 4) Пусть f(X)
назыв сходящ и равен ему. 4) Пусть f(X)
Непрерыв на (а;b]. Возьмем Е>0.Рассмотр 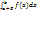 =F(b)-F(a+E). lim(E→0+0)F(b)-F(a+E).
=F(b)-F(a+E). lim(E→0+0)F(b)-F(a+E).
(4) Опр:если есть конеч пред (4) то несобст интегр сходится и равен этому пределу.3) пусть f(x)
непрер на [a,c) v (c,b]. Е>0 и Ϭ>0. Рассмотр 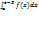 =F(c-E)-F(a) и
=F(c-E)-F(a) и 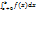 =F(b)-F(c+Ϭ)
=F(b)-F(c+Ϭ)
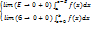 (5 ) Опр: еси есть оба конеч предел (5) ,то интегр
(5 ) Опр: еси есть оба конеч предел (5) ,то интегр 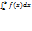 сходит
сходит
И равен их сумме.если хотя бы 1 из них не сущест или равен ∞ то расходится.
30)Опр: пусть D это нек множ-во в простран-ве Rn-ая, а U-мн-во действ чисел. Если в кажд т.МЭD поставлена
В соответ с нек прав число u из U, то гов, что зад ф-я неск перемен u=f(M)/Граф ф-и 2 переменн Z=f(x,y)
это мно-во точек трехмерного пространства (x,y,z),аппликата z которых связана с абсциссой х и ординатой у
функциональным соотношением Z=f(x,y).Это некоторая поверхность в трехмерном пространстве.
Опр:линией уровня ф-и 2 аргументов Z=f(x,y) назыв множ-во точек на плоскости,где значен ф-и одно и тоже и = С.
С-это уровень. Лин ур-ня служит семейство параллельн прямых.Лин ур-ня производственной ф-и-это изокванты.Опр: число А
это предел фции Z=f(x,y) при х→х0 и у→у0 если для любого,даже сколь угодно малого положит числа Σ
найдется полодит число Ϭ (зависящее от Σ) такое,что для всех точек (х,у),отстоящих от точки (х0,у0) на
расстояние Р (при 0<Р<Ϭ) выполняется нер-во |f(x,y)-A|<Σ.Обозначается предел так 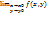 =A
=A
Опр:ф-я Z=f(x,y) назыв непрер в точке (х0,у0) если она:1) определена в точке (х0,у0) 2) имеет конеч
предел при х→х0 и у→у0 3) этот предел равен значен ф-и в точке (х0,у0),т е 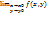 =f(x0,y0)
=f(x0,y0)
31)Опр:частной произв ф-и неск арг по 1 из этих арг назыв предел отношен соответс частного
приращ ф-и к приращ арг при его стремлен к 0.Обозначается: u ’x Опр:частным диф-м назыв сумма
произв частных произв этой ф-и на приращения соответствующих независимых прем-х:
dz= z’x∆x+ z’y∆y. Полный диф-ал-это линейная,относительно ∆х ∆у часть полного приращения ф-и.
du=dxu+dyu.Опр: фция Z=f(x,y) назыв диф-мой в точке (х,у) если ее полное приращен может быть
представлено виде ∆z=dz+α∆x+β∆y. Где dz-диф-ал ф-и, α=α(∆х,∆у), β=β(∆х,∆у)-бесконеч малые при ∆х→0
∆у→0.
33)Опр: точка М(х0,у0) назыв точ макс(мин) ф-и Z=f(x,y) если есть окрестность точки М,такая что для всех точек (х,у) из этой окрестности выполн нер-во f(x0,y0)  f(x,y) (f(x0, y0)
f(x,y) (f(x0, y0)  f(x,y)). Теорема:Необходим услов экстремума:если точка М это точка максим(миним) то частные произ-ные в Этой точке = 0.Теорем:Достотач условие: пусть ф-я Z=f(x,y): а) определена в некоторой окрестности критической точки (х0,у0) в которой fх ’(x0,y0)=0 и fу ’(x0,y0)=0 б) имеет в этой точке непрерывные частные производные второго порядка f xx’’(x0,y0)=A, f xy’’(x0,y0)=B, f yy’’(x0,y0)=C,тогда если ∆=АС-В2>0 то в точке (х0,у0) ф-я имеет экстремум,причем если А<0-максимум, А>0-минимум.
f(x,y)). Теорема:Необходим услов экстремума:если точка М это точка максим(миним) то частные произ-ные в Этой точке = 0.Теорем:Достотач условие: пусть ф-я Z=f(x,y): а) определена в некоторой окрестности критической точки (х0,у0) в которой fх ’(x0,y0)=0 и fу ’(x0,y0)=0 б) имеет в этой точке непрерывные частные производные второго порядка f xx’’(x0,y0)=A, f xy’’(x0,y0)=B, f yy’’(x0,y0)=C,тогда если ∆=АС-В2>0 то в точке (х0,у0) ф-я имеет экстремум,причем если А<0-максимум, А>0-минимум.
34)Опр:произв ф-и u=f(x,y) по направлению L назыв предел отношен приращен ф-и в направлен L к велечине приращения ∆L,при ∆L→0(лист).Опр: Градиентом ф-и u=f(x,y) назыв вектор,коорд которого = част произв ф-и.(grad u). Св-ва градиента:1)Произв ф-и u по зад направл L проекции вектор град на это направл(лист)Вектор град в кажд точке по велич и направл соответсв наиб скорости возраст ф-ии в этой точке
35)Опр: числов рядом назыв выраж вида u1,u2,…,un…соединенных знаком сложения:
u1+u2+…+un+…= 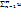 n Опр: если есть конеч предел последоват част сумм числового ряда (S1;S2 ,…Sn) то этот предел назыв суммой числового ряда,а ряд назыв сход. Если предел не сущ или обращ в ∞ то ряд расход. Теорема: Необходимый признак сходимости: Если числовой ряд сходится то его предел его общего члена = 0.Св-ва сходящихся рядов:1) если ряд u1+u2+…+un..сходится и имеет сумму S то и ряд αu1+αu2+…+αun (полученный умножением ряда на α) также сходится и имеет сумму αS.2) если ряды u1+u2+…+un и v1+v2+…+vn сходится и их суммы соответственно равны S1 И S2 то и ряд (u1+v1) +(u2+v2)+…+(un+vn) (это сумма данных рядов) также сходится и его сумма равна S1 + S2 3) если ряд сходится,то сходится и ряд получ из данного путем отбрасывания (или приписывания) конечного числа членов.
n Опр: если есть конеч предел последоват част сумм числового ряда (S1;S2 ,…Sn) то этот предел назыв суммой числового ряда,а ряд назыв сход. Если предел не сущ или обращ в ∞ то ряд расход. Теорема: Необходимый признак сходимости: Если числовой ряд сходится то его предел его общего члена = 0.Св-ва сходящихся рядов:1) если ряд u1+u2+…+un..сходится и имеет сумму S то и ряд αu1+αu2+…+αun (полученный умножением ряда на α) также сходится и имеет сумму αS.2) если ряды u1+u2+…+un и v1+v2+…+vn сходится и их суммы соответственно равны S1 И S2 то и ряд (u1+v1) +(u2+v2)+…+(un+vn) (это сумма данных рядов) также сходится и его сумма равна S1 + S2 3) если ряд сходится,то сходится и ряд получ из данного путем отбрасывания (или приписывания) конечного числа членов.
36) Теорема: Необходимый признак сходимости:Если числовой ряд сходится то его предел его
общего члена равен 0.Док-во: u1+u2+…+un+…= 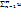 n сходится.
n сходится. 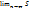 n=S
n=S
Рассмотрим Sn= u1+u2+…+un-1+un u1+u2+…+un-1=Sn-1 Следовательно: un=Sn-Sn-1
lim(n→∞)un=lim(n→∞)( Sn-Sn-1)=S-S=0.Неох призн сход достат не явл, если
для ряда выполн необх услов сход, то ряд м. сход и расход Примером служ гарм
ряд. Опр:Гарм рядом называют сумму бесконечного количества членов обратных
последовательным числам натурального ряда. Например:1+1/2+1/3+…+1/n. Гармонический
ряд есть ряд расходящийся, т.е. сумма первых n его членов неограниченно растет с ростом
количества взятых членов. Однако в отличие от других расходящихся рядов скорость роста суммы с увеличением
числа членов замедляется. Гармонический ряд называют слабо расходящимся по сравнению с ростом n.
37)Достаточные признаки сходимости знакопол рядов: 1)признак сравнения: пусть
даны 2 ряда с положит членами 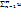 n (1) и
n (1) и 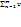 n (2) причем члены 1 ряда не
n (2) причем члены 1 ряда не
превосходят членов 2,т е:un  vn тогда: если сходится (расходится) ряд 2,то сходится (расходится)
vn тогда: если сходится (расходится) ряд 2,то сходится (расходится)
и ряд 1; Док-во:пусть сходится 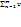 n , Un- частич сумма 1 ряда, Vn- частич сумма 2 ряда. Т.к
n , Un- частич сумма 1 ряда, Vn- частич сумма 2 ряда. Т.к
un  vn то , Vn
vn то , Vn  Un тк 2 ряд сходится то lim(n→∞) Vn=V ; Un И Vn возрастающие ,
Un тк 2 ряд сходится то lim(n→∞) Vn=V ; Un И Vn возрастающие ,
Un  Vn
Vn  V то Un
V то Un  V, Un-возрастающ огранич сверху. Lim(n→∞) Un= U -1 ряд тоже
V, Un-возрастающ огранич сверху. Lim(n→∞) Un= U -1 ряд тоже
сходится.2) признак Даламбера: если есть конеч предел последующего члена законоположит ряда
к предыдущему 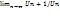 =L то при L<1 сходится,а при при L>1 расходится,и при
=L то при L<1 сходится,а при при L>1 расходится,и при
при L=1 признак Даламбера ответа не дает.
38)Опр:ряд называется абсолютно сход,если сходится как сам ряд,так и ряд,составленный
из абсол велечин его членов.Опр:ряд назыв условно сходящимся,если сам ряд сходится,а
ряд составленный из абсолютных велич его членов расход.Опр: под знакочередующимся
рядом понимается ряд,в кот члены попеременно то полож,то отриц:
U1-U2+U3-U4+…+(-1)n-1Un… где Un>0.Признак Лейбница:если абсолютный велич
Членов знакочередующ ряда монотонно убывают с ростом номера n и V1>V2>…>Vn>Vn+1>…
И предел Vn =0 то такой знакочередующийся ряд сходится,по крайне мере условно.
39)Опр:Функциональные ряды-это ряды,членами которых служат фции: V 1 (х)+ V 2 (х)+…+
Vn (х)= 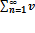 n (х). Область определе функционал ряда-это множ-во значений Х при котор
n (х). Область определе функционал ряда-это множ-во значений Х при котор
Определены все члены функционал ряда.Область сходимости числового ряда это множ-во знач
Х при которых функционал ряд превращается в сходящийся числовой ряд. S ( X )-это сумма функц
Ряда,которая определена на области сходимости.Опр:стпенной ряд-это ряд вида : а0+а1х+
+а2х2+…+а n xn +… Область сходимости:совокупность значений,где степенной ряд сходится.
Ее структура устанавливается по теореме Абеля.Опр:Интервал вида (- R ; R ) R 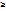 0 внутри которого
0 внутри которого
Степен ряд сходится,а вне котор расходится назыв интервалом сходимости,а R -радиусом.
Теорема Абеля:Если степенной ряд сходится при х=х1,то этот ряд будет сходится абсолютно при
Всех | x |<| x 1|.Если степенной ряд расходится при х=х2, то он будет расходится при всех | x |>| x 2|
40)Интегрир и диффер степен рядов:в области сходимости степ ряда,степ ряды по отношению к
Оперециям интегрир и диффер-ания ведут себя как обычные многочлены. Степенной ряд можно
почленно интегрировать по любому отрезку [a, b], принадлежащему интервалу сходимости.
В частности, ряд можно почленно интегрировать в пределах от 0 до x, где |x| < R.Ряд Маклорена:
Пусть f ( x ) определена и n раз диф-ема в окрестности точки х=0, разложим ее в степенной ряд:
F ( x )= а0+а1х+а2х2+…+а n xn +…+ а n +1 xn +1 +… Найдем произ-ные фции,почленно диф-руя
Ряд n раз : f ’(x)=0+a1+2a2x+3a3x2+4a4x3+…nanxn-1+(n+1)an+1xn… f ’’=2a2+
+6a3x+12a4x2+n(n-1)anxn-2+n(n+1)an+1xn-1…f ’’’(x)=6a3+24a4x+…+
+n(n-1)(n-2)anxn-3+n(n+1)(n-1)an+1xn-2… f(n)(x)=n(n-1)(n-2)∙…2an+(n+1)…
∙2an+1x… Пусть х =0. Получим f(0)=a0 f ’(0)=a1 f ’’(0)=2a2 f ’’’(0)=3!(a3) f n=n!(an).
Выразим везде а.и подставим полученное а в f ( x ) : f ( x )= f (0)+ f ’(0) x + f ’’(0)/2! ∙ x 2 +
+ f ’’’(0)/3! ∙ x 3 +…+ f ( n ) / n ! ∙ xn Разложение в ряд 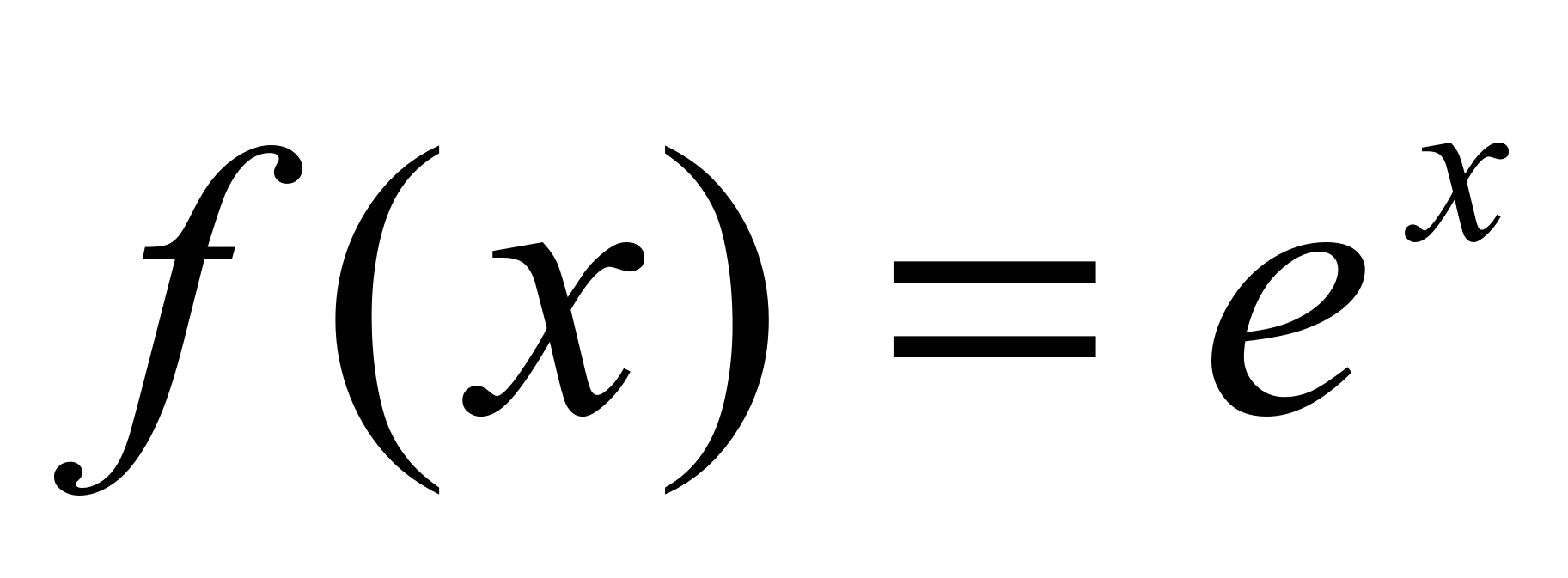 . Значения фции и ее произ-ных
. Значения фции и ее произ-ных
в точке x =0 равны: 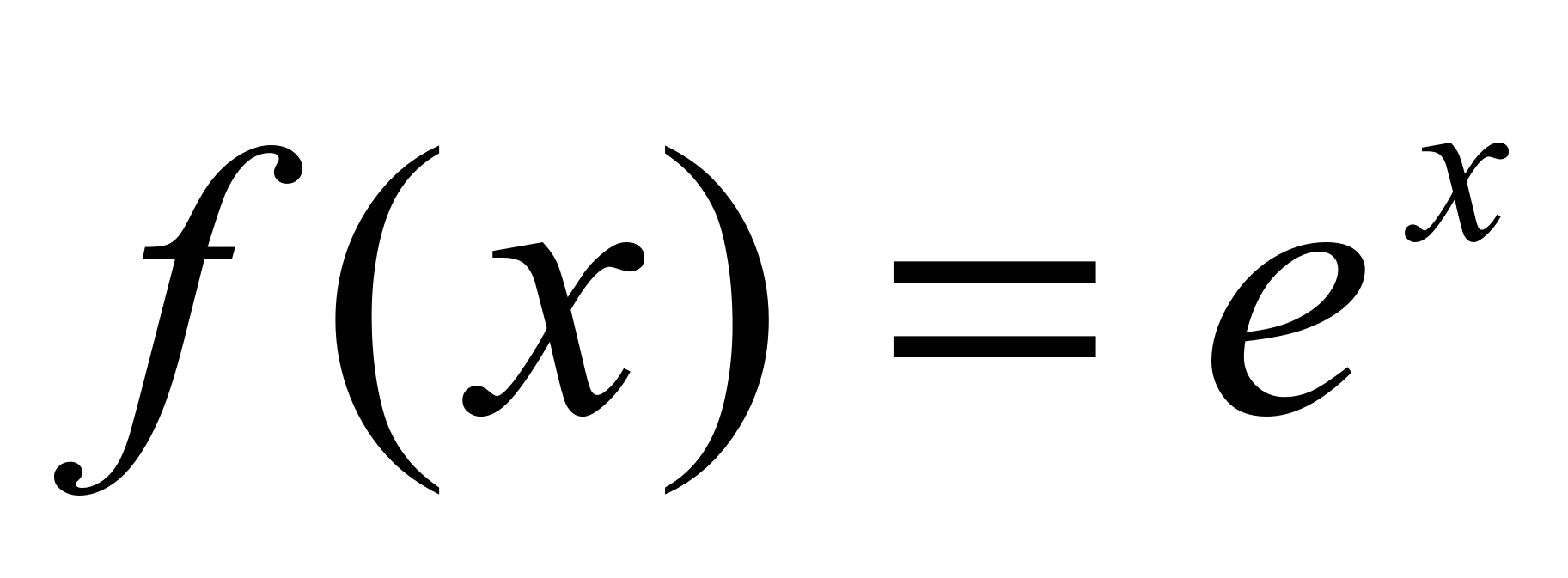
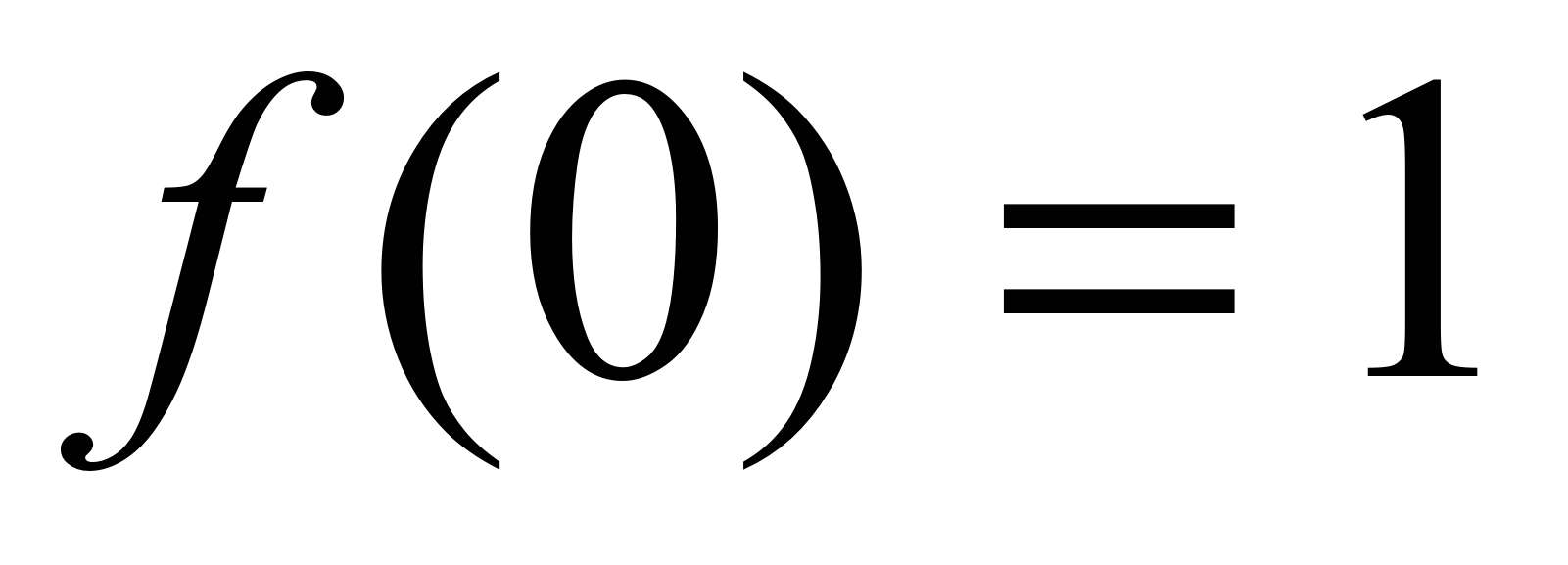
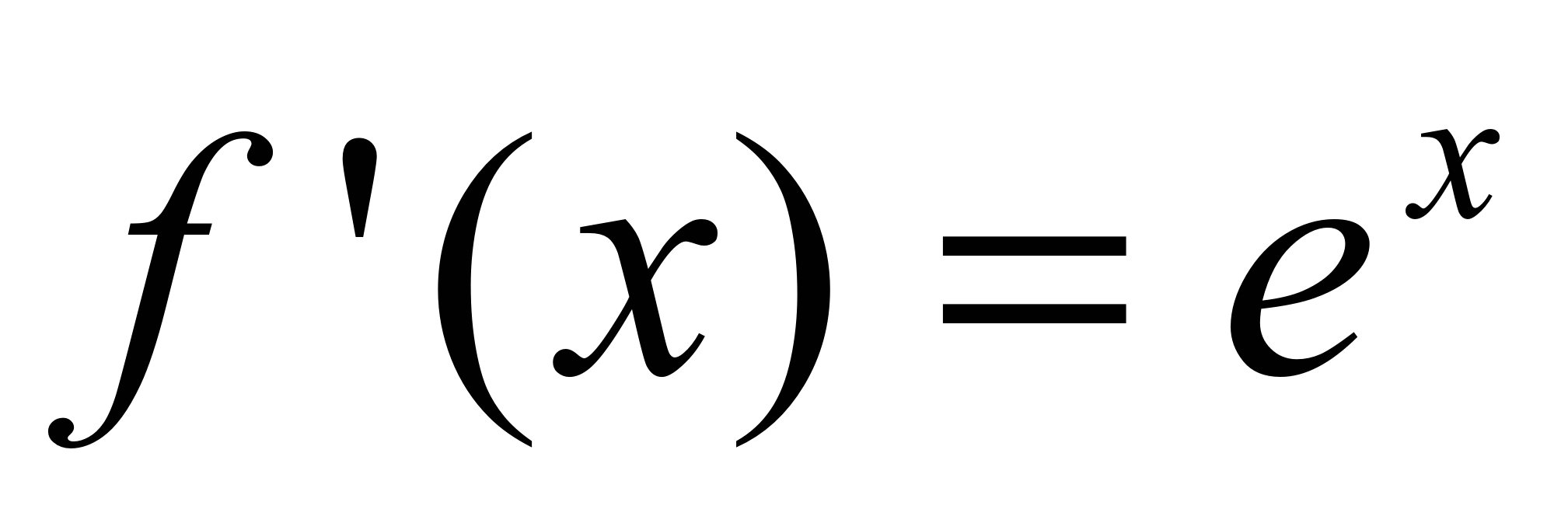 ,
, 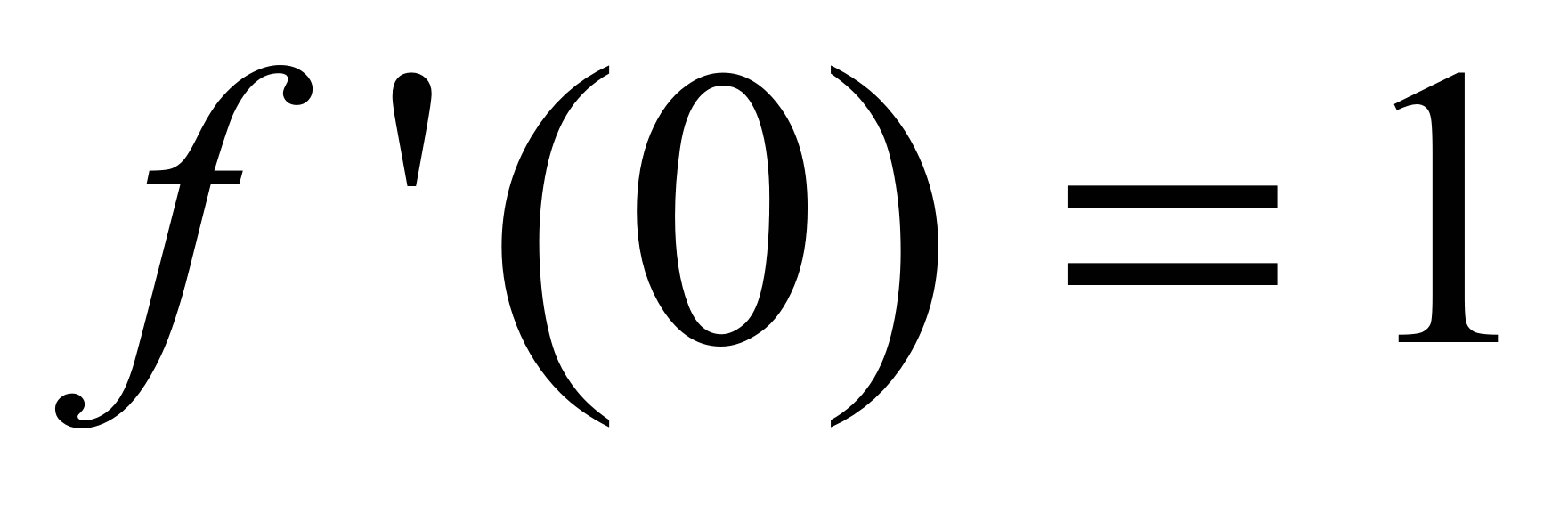 ,
,
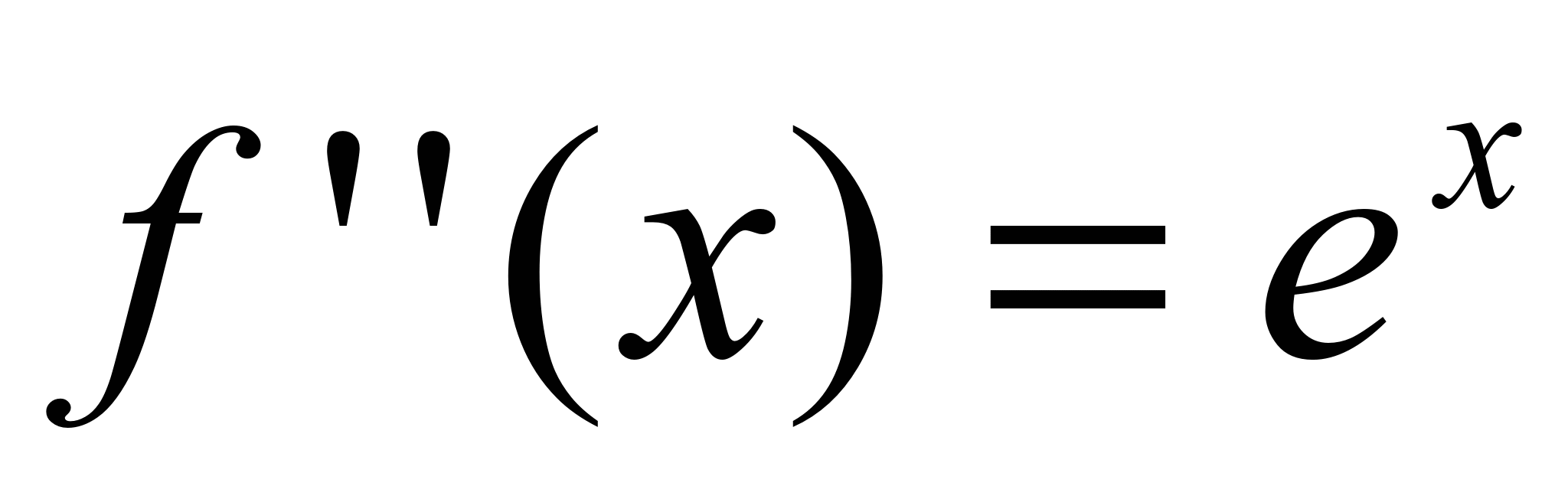 ,
, 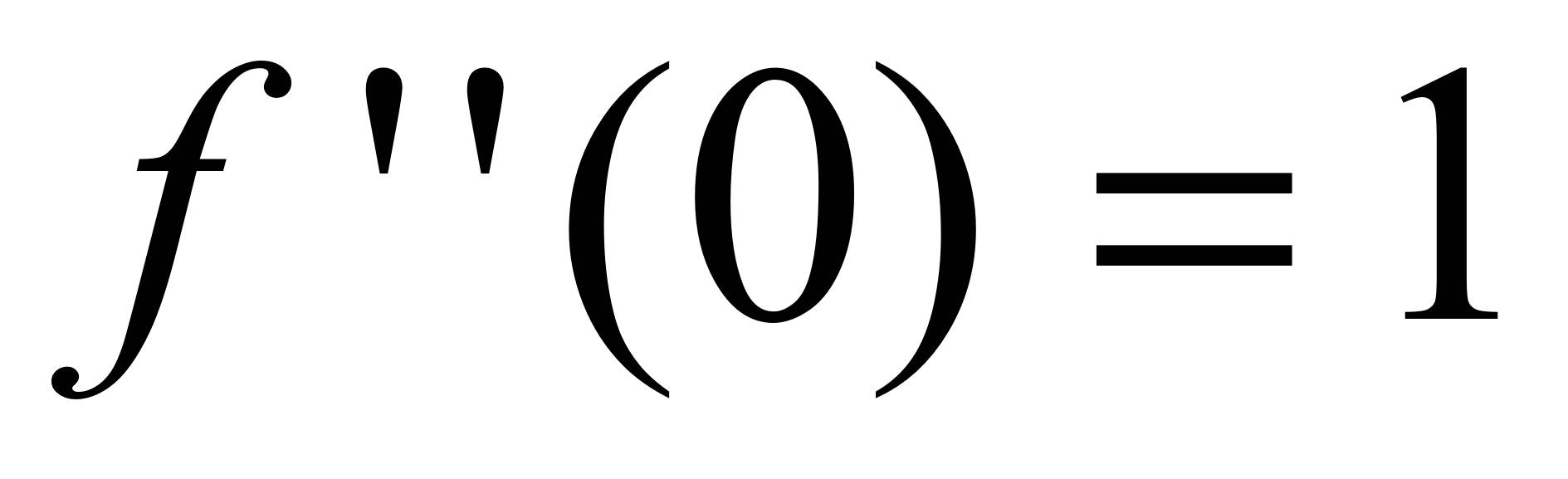 ,
, 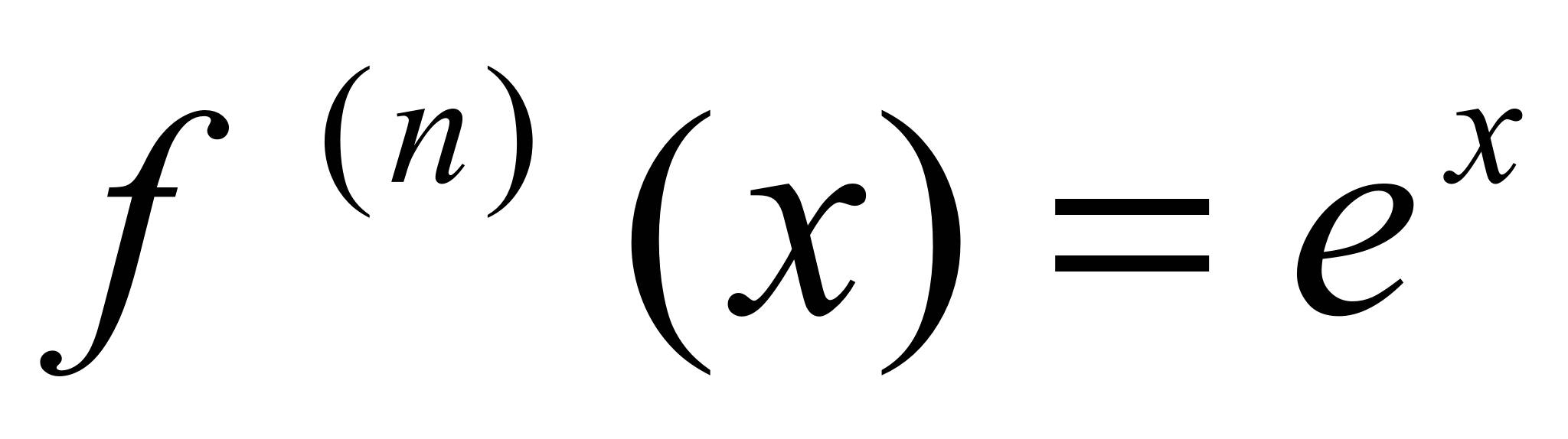 ,
, 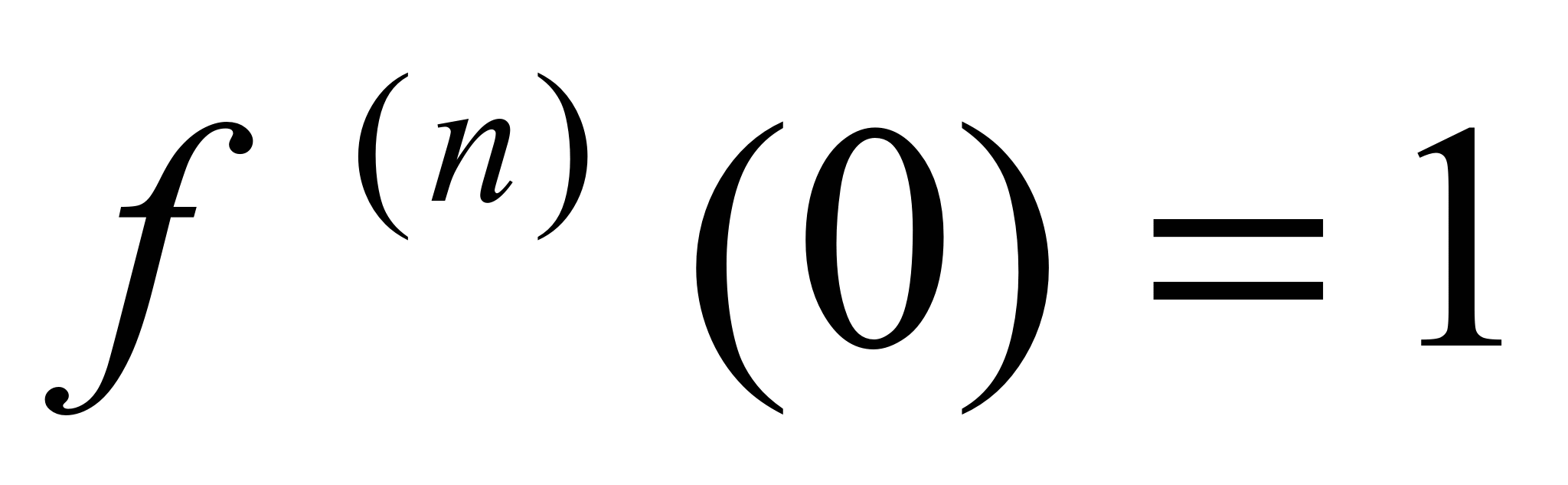 ,так что ряд
,так что ряд
Маклорена принимает вид 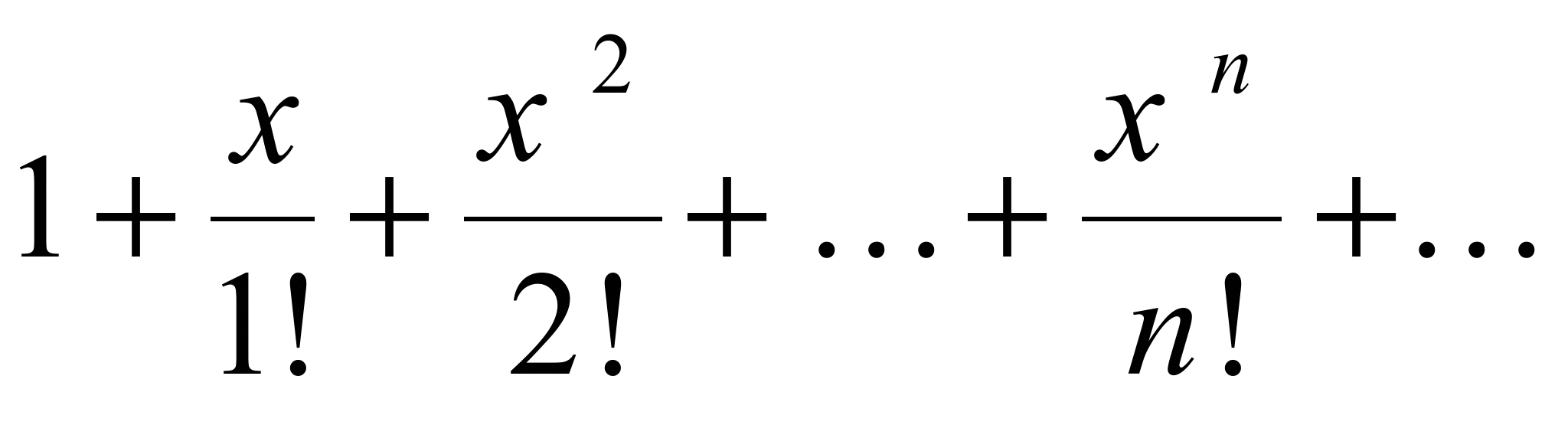 .Радиус сходимости этого ряда
.Радиус сходимости этого ряда
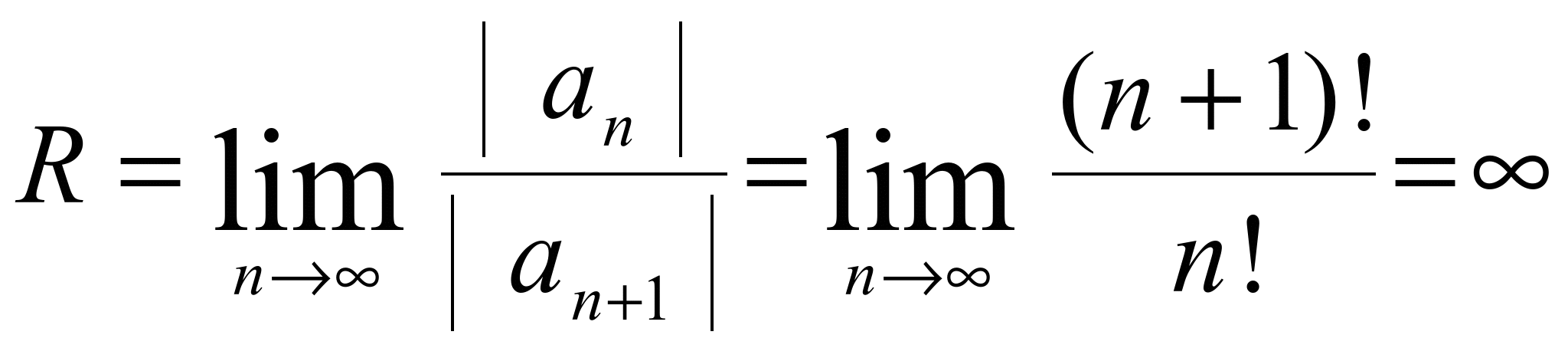 ,то есть ряд абсолютно сходится на
,то есть ряд абсолютно сходится на
всей числовой оси.
Разложение 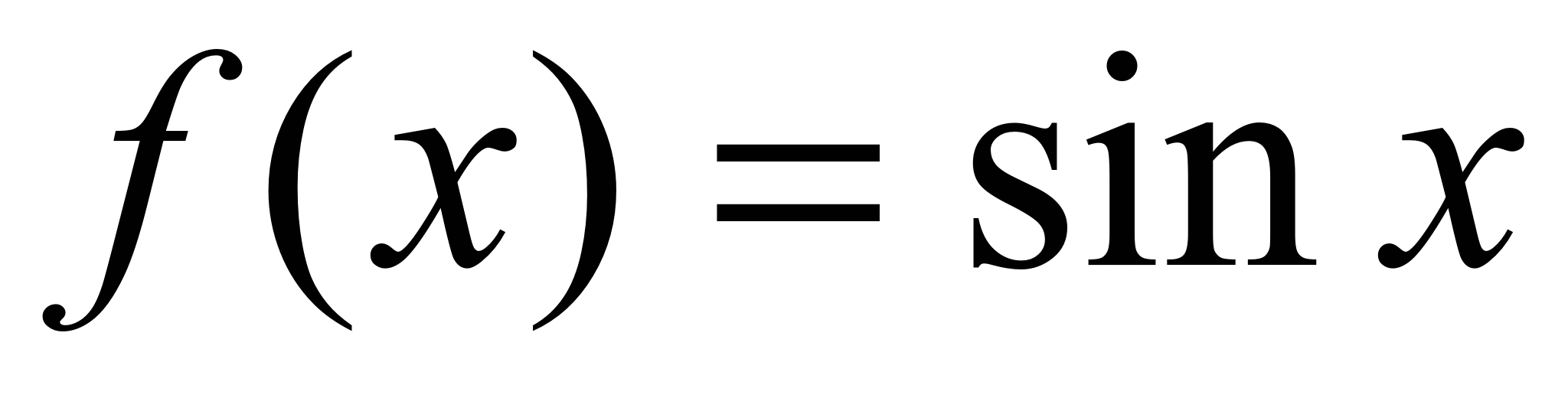 .Находим:
.Находим: 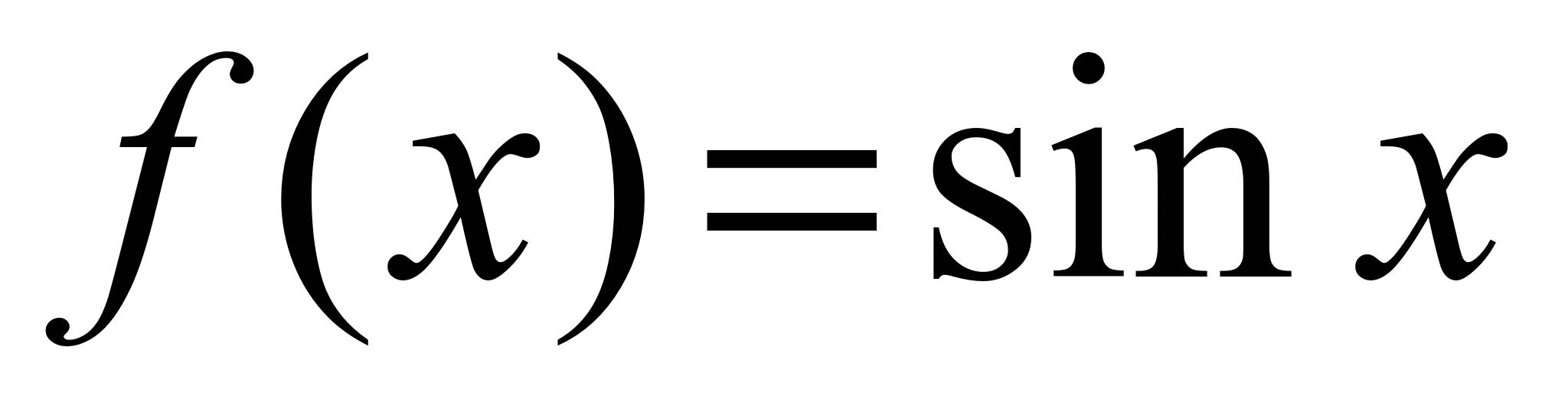 ,
, 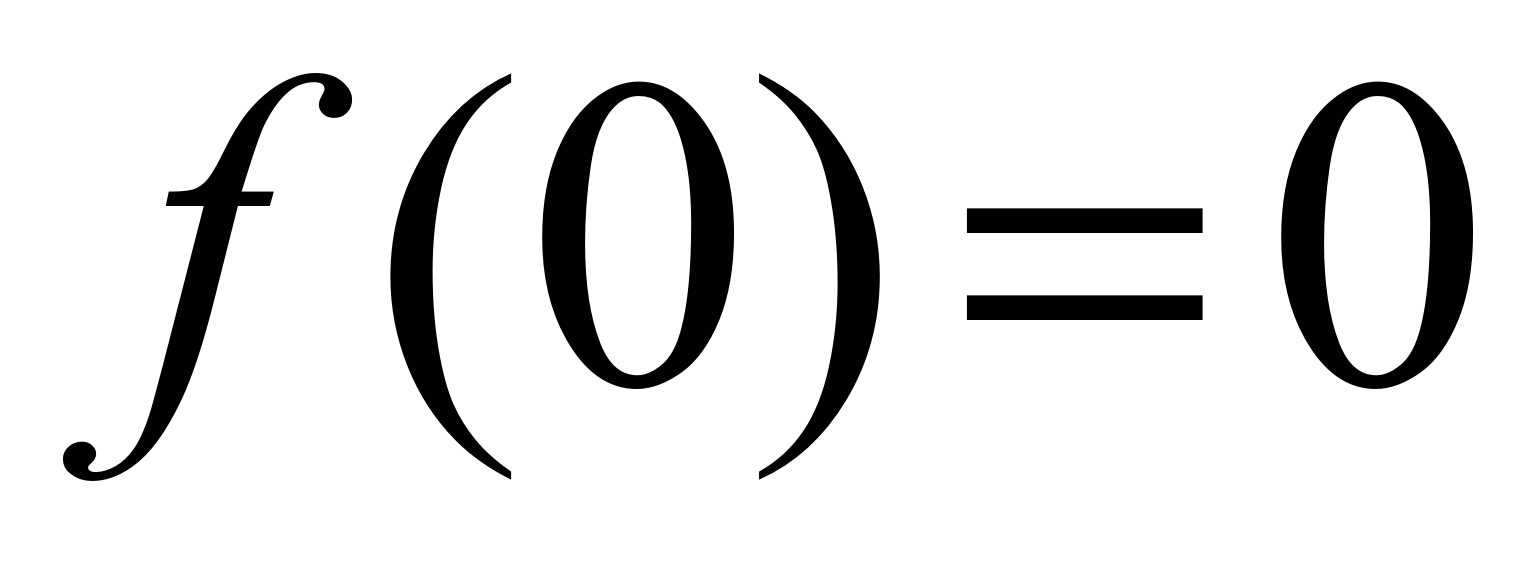
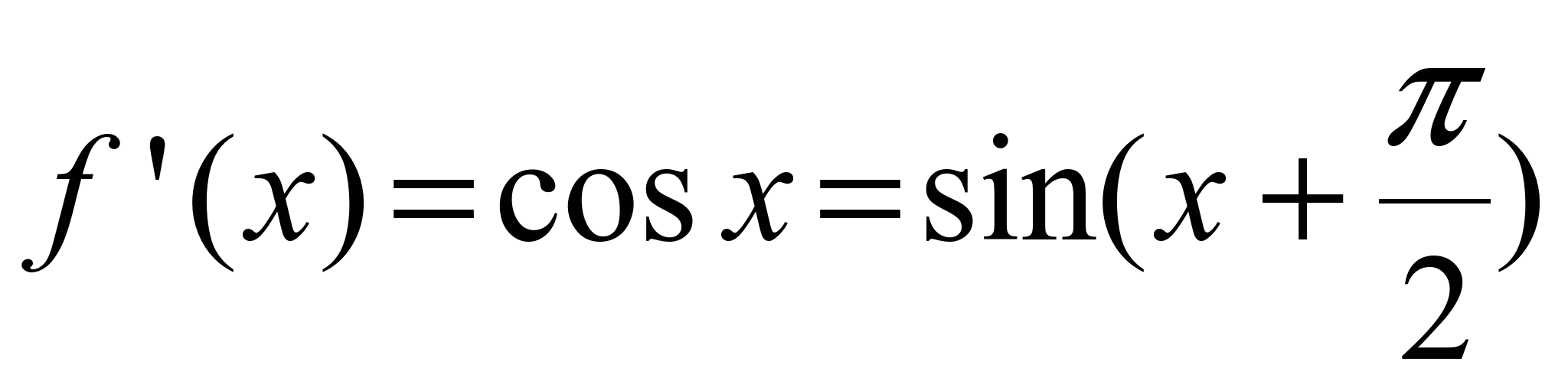 ,
, 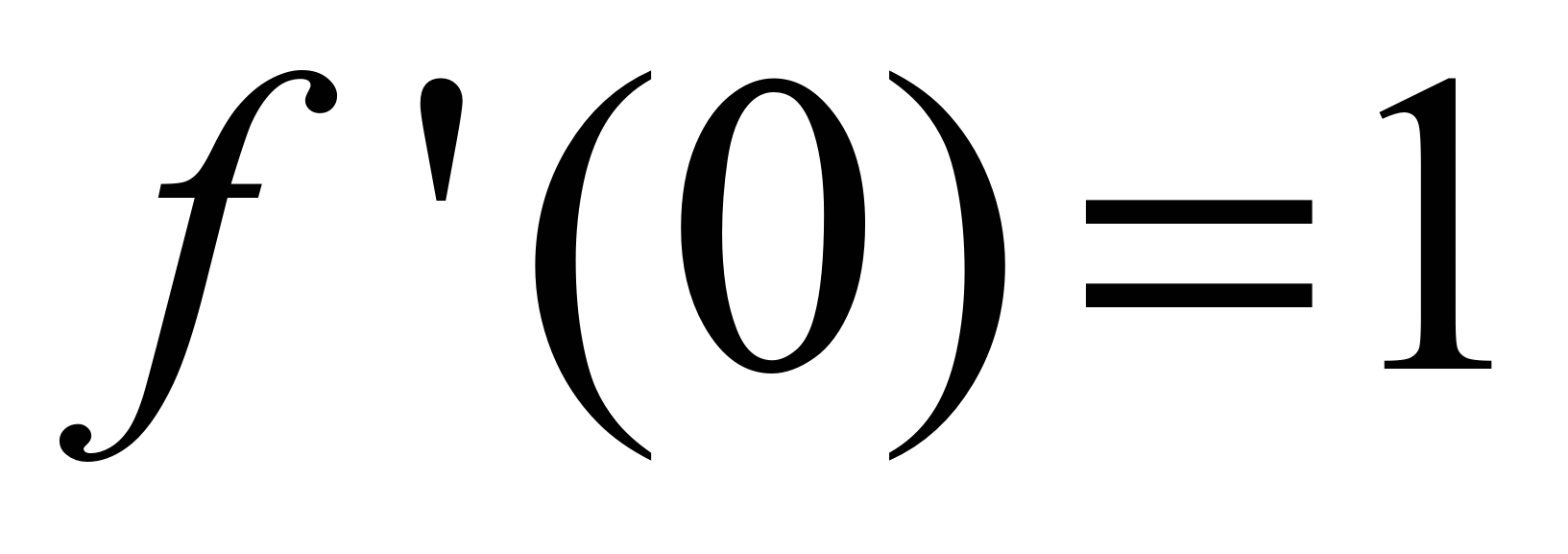 ,
, 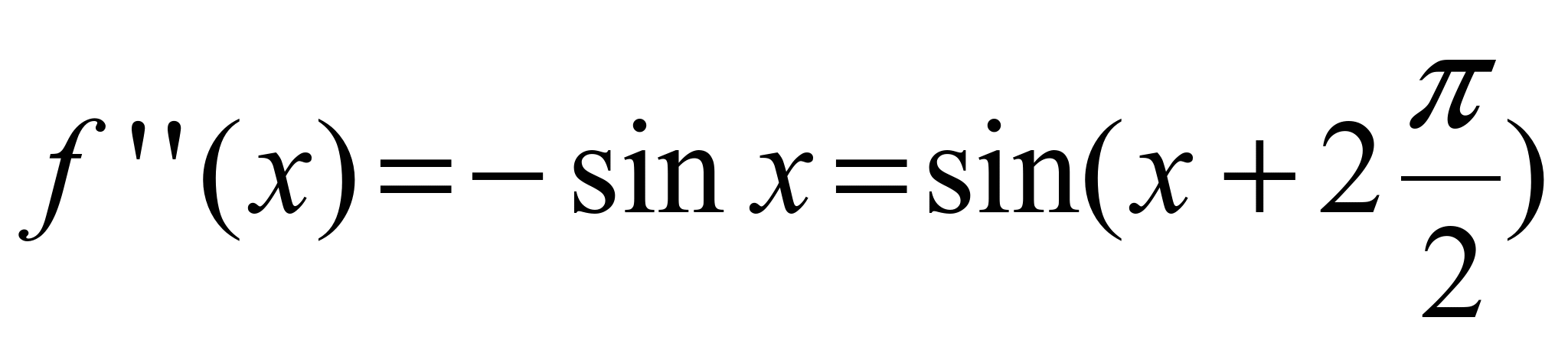 ,
,
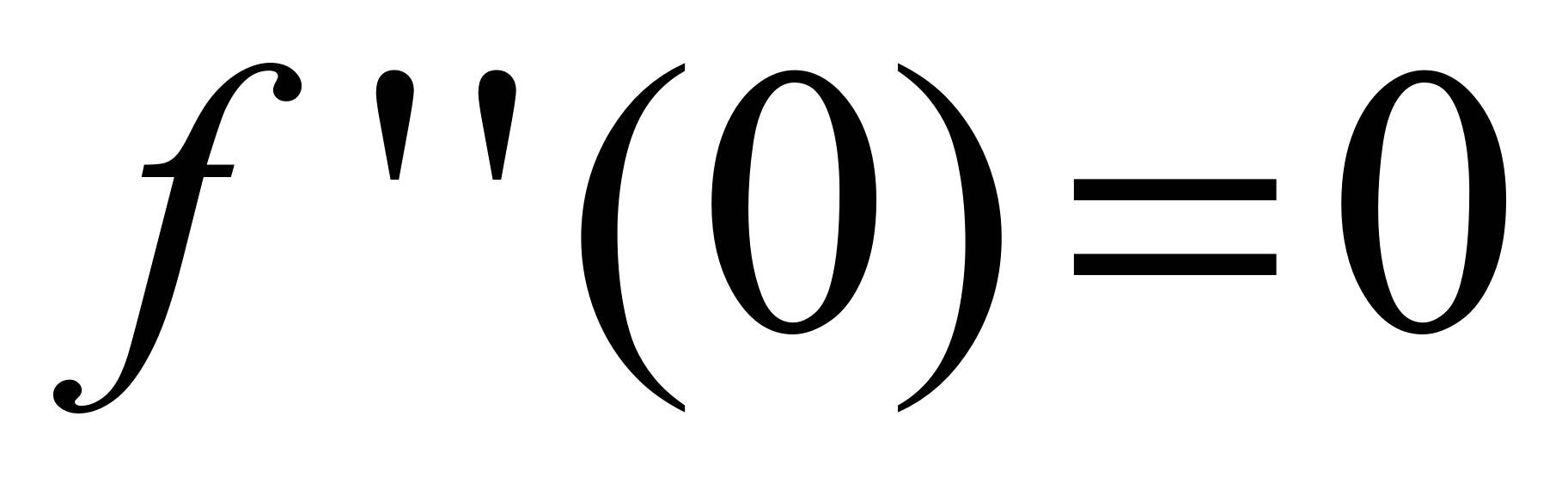 ,
, 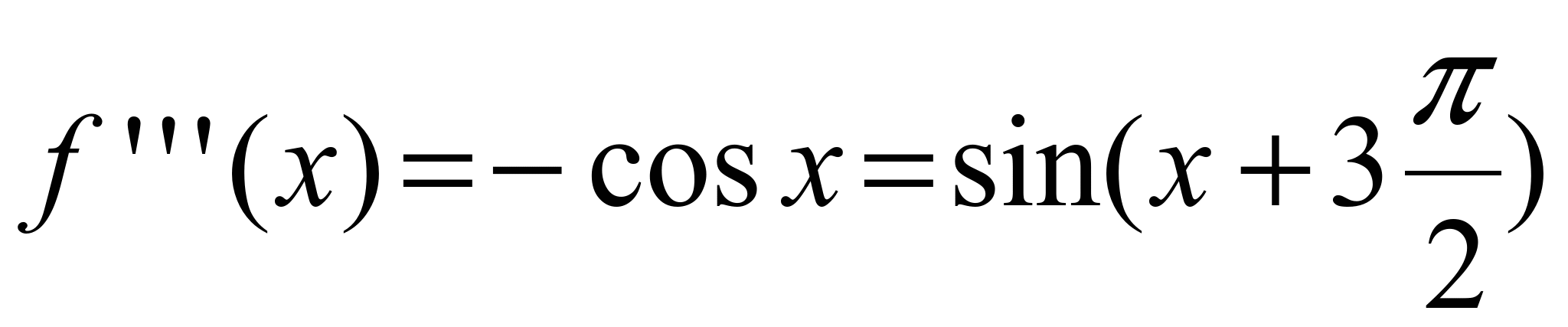 ,
, 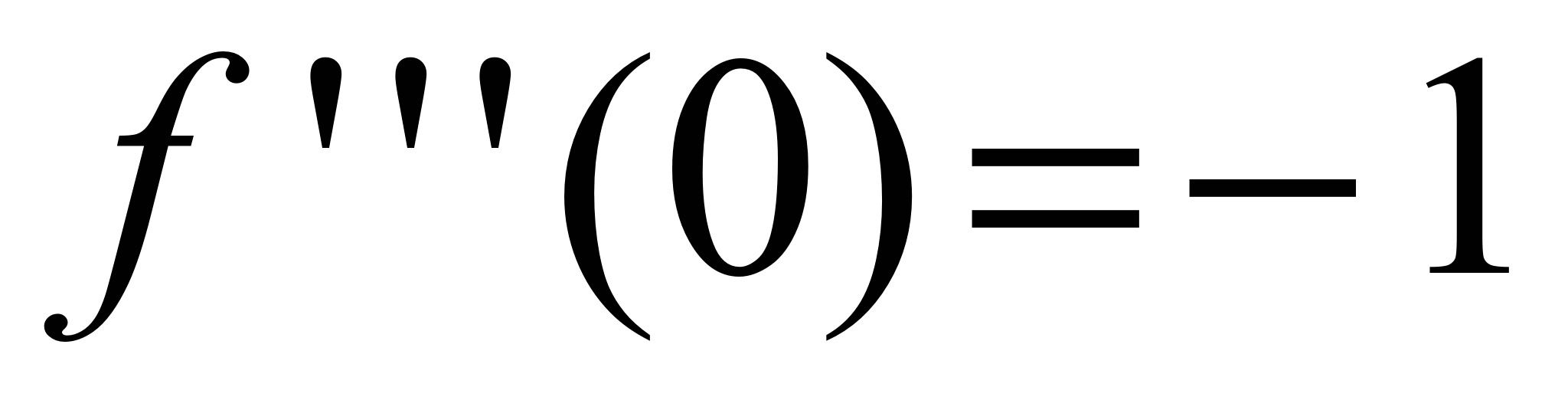
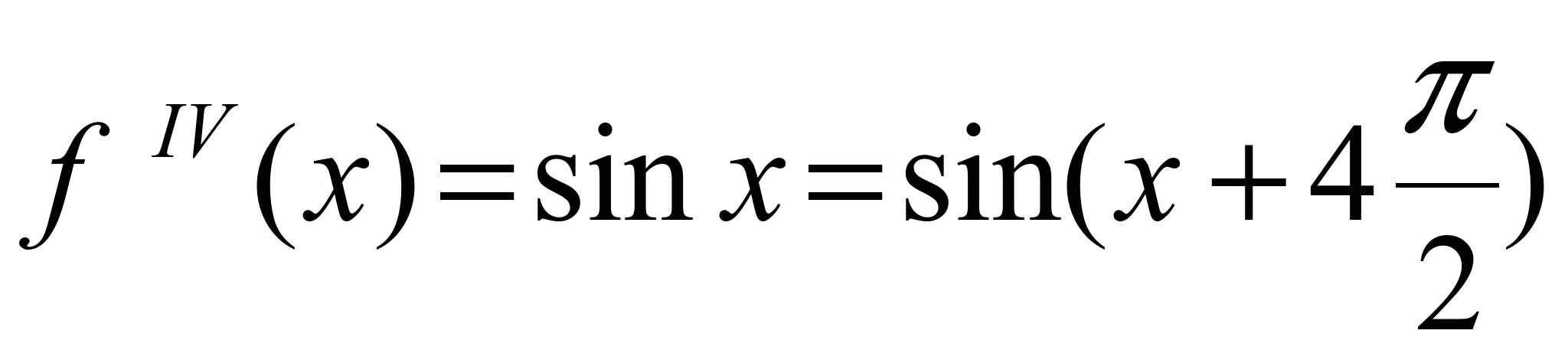 ,
, 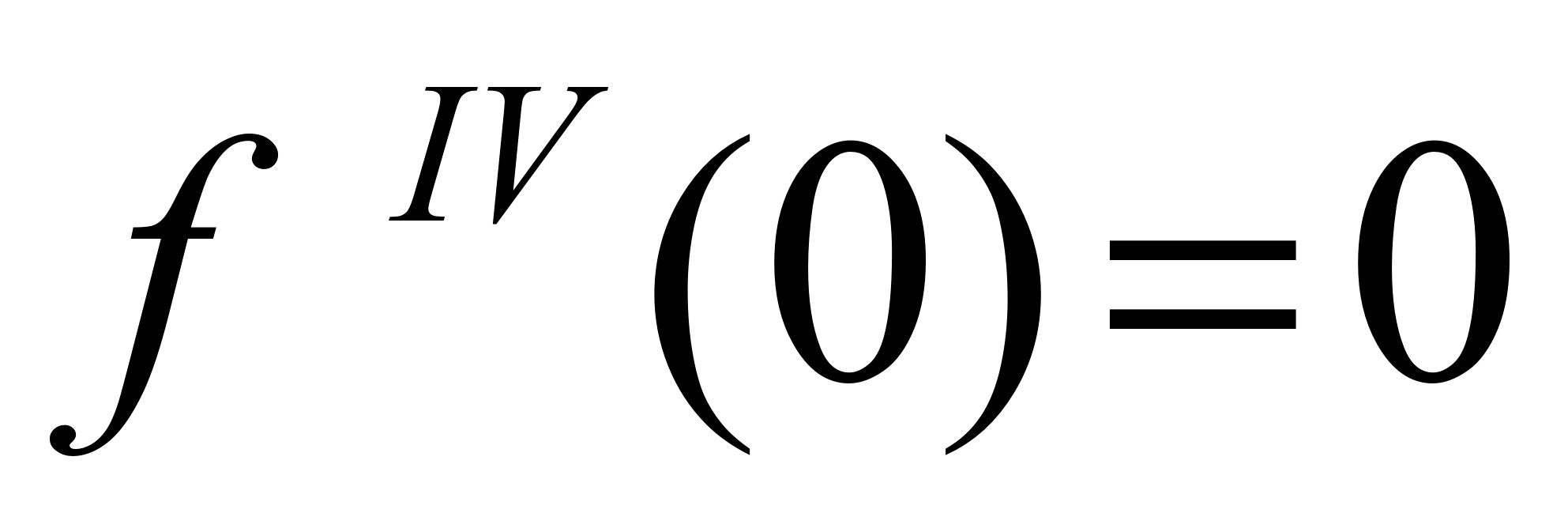 ,
, 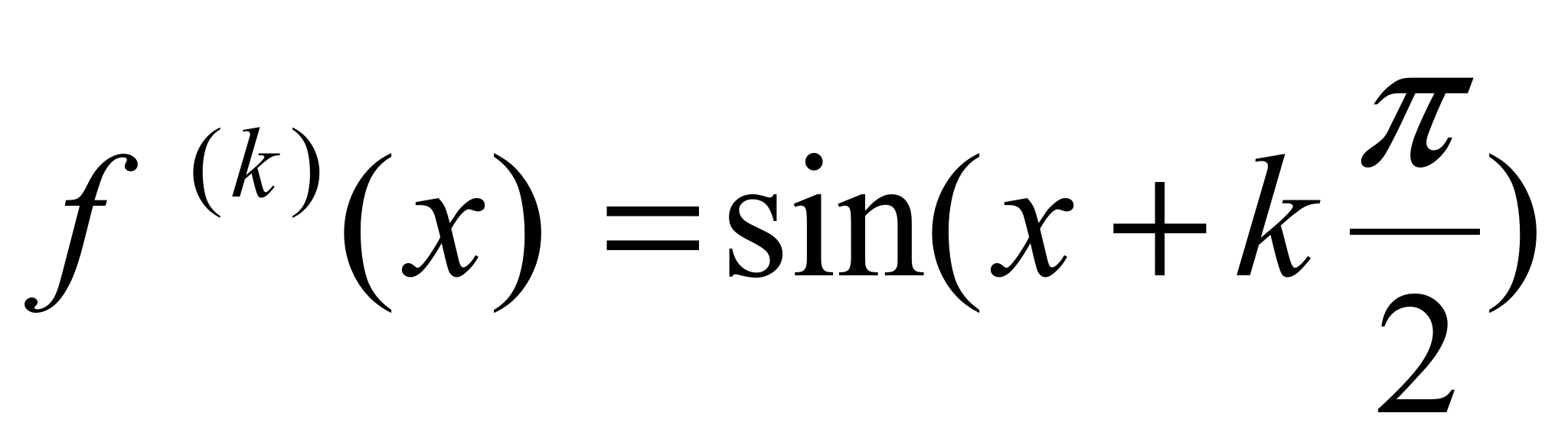 ,
,
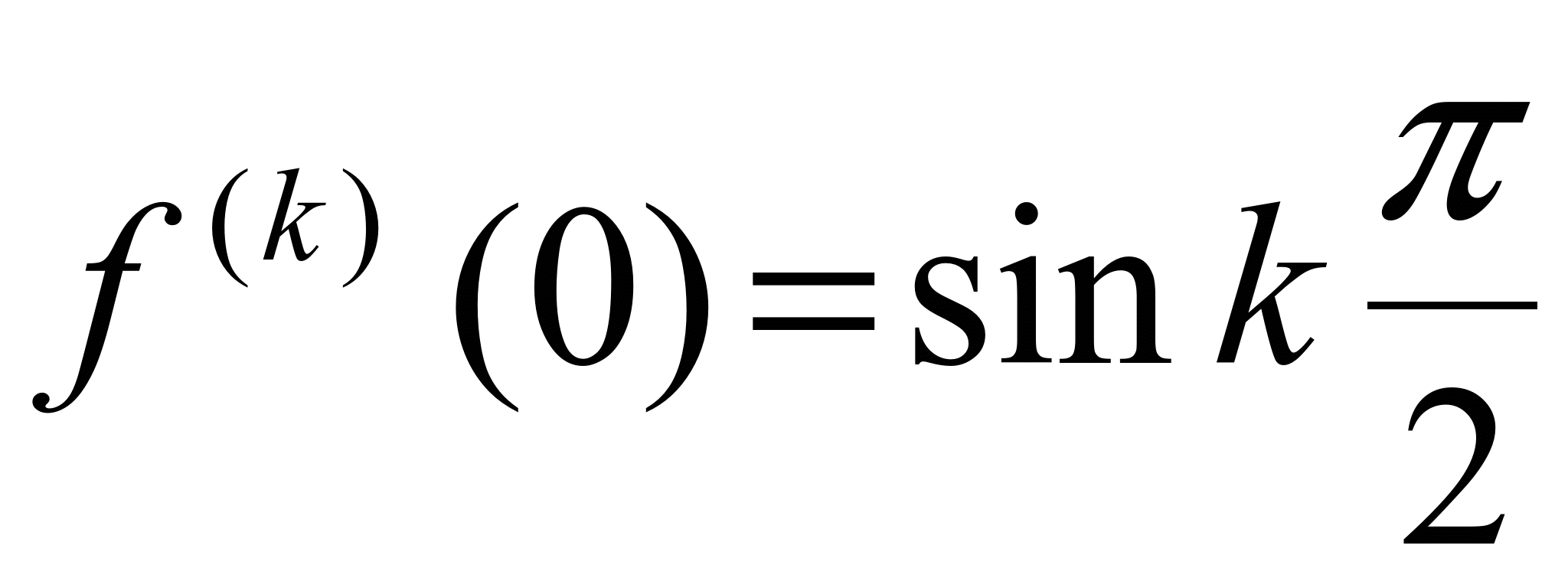 .получаем
.получаем 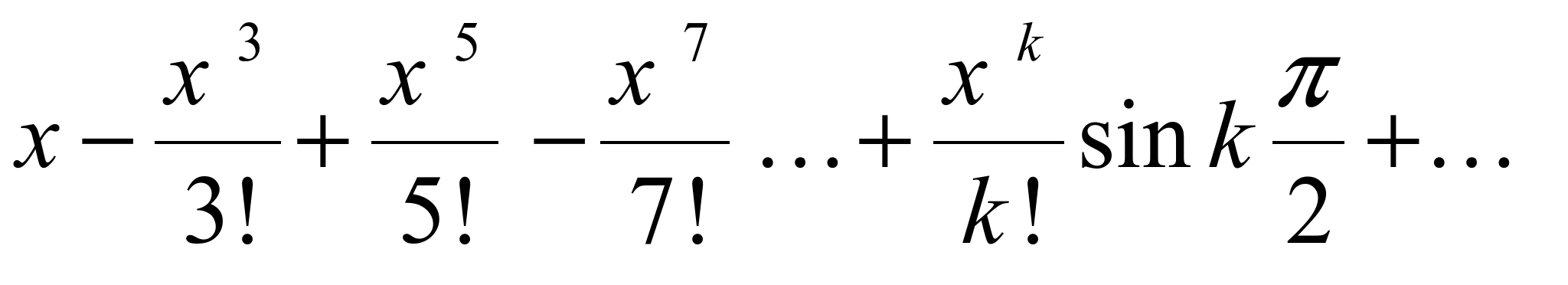
в котором члены с четными k отсутствуют.По этой причине удобно
положить 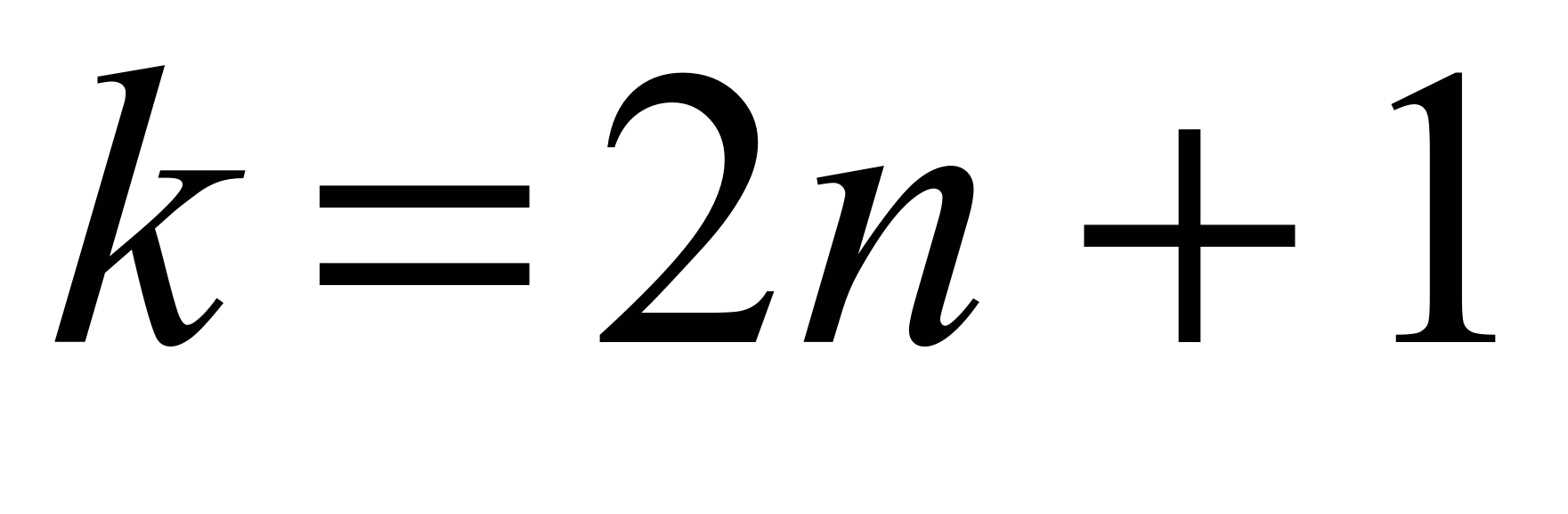 ,
,  .
.
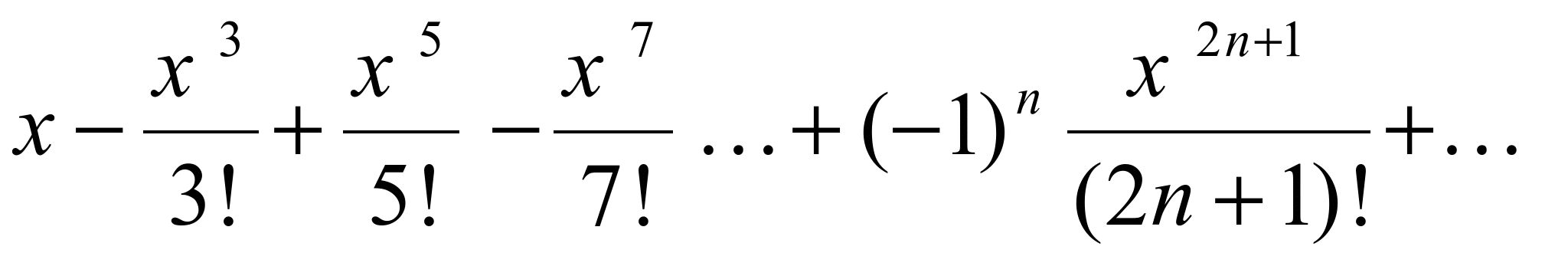 .
.
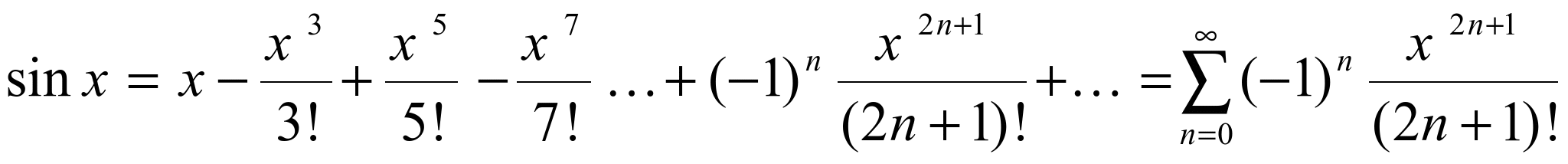 .
.
P азложение 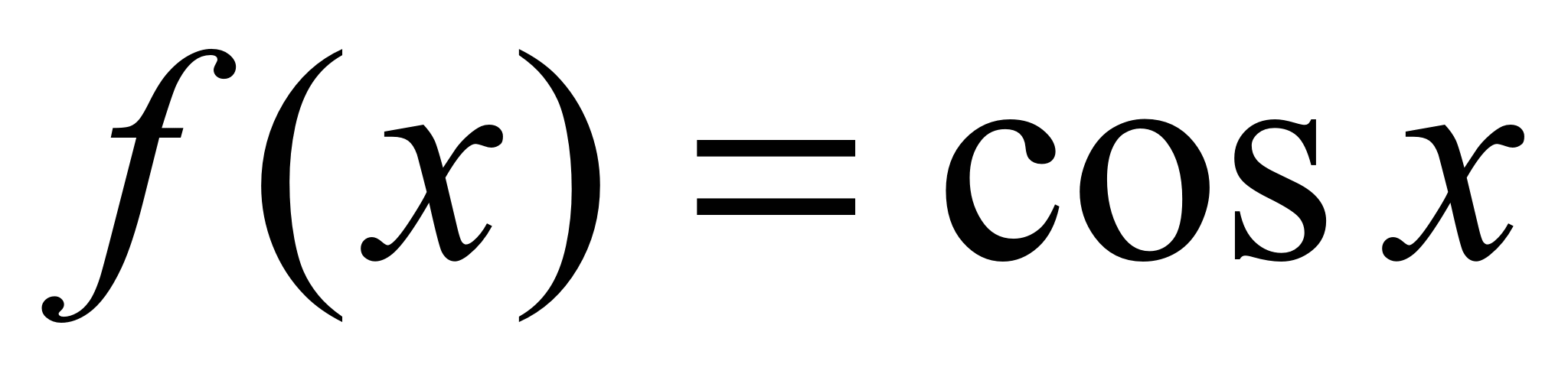 .Разложение этой функции в ряд Маклорена проводится аналогично
.Разложение этой функции в ряд Маклорена проводится аналогично
предыдущему и ряд имеет вид
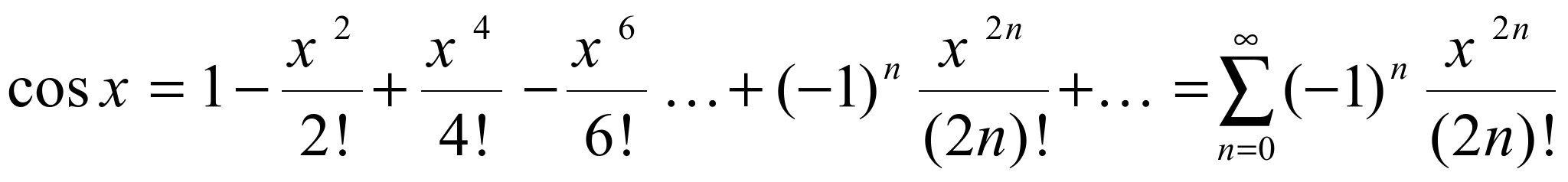 .
.
32) Берем фцию u=f(x,y) даем приращение ∆х, попадаем в точку (х+∆х; у) тогда фция u получила
приращение по х (ux).∆ x u / u -относит изменен фции. ∆ x / x -относит изменен аргумента.Найдем
предел: lim ( x →0) (∆ x u / u )/ ∆ x / x = lim ( x →0) x ∆ x u / u ∆ x = x / u lim ( x →0)∆ x u /∆ x =
= x / u ∙ u ’ x = Exu . Exu -эластич фции u по х.Опр:Эластич фции u по х назыв предел отношения
относит изменен фции к соответст относит изменен аргумента.Эластич фции Кобба-Дугласа:
y =α0 Lα 1 Kα 2
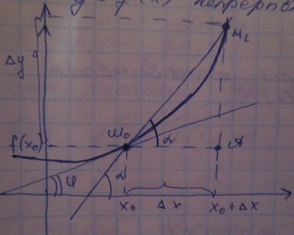
10) Пусть на плоскости хОу дана кривая уравнением у = f (х). M 0 M 1-секущая.Устремляем
М1 к М0 вдоль кривой М1→М0,секущая крутится вокруг М0,получаем касательную.
Касательной к графику фции в точке с асциссой х0 называют предельное полодение М0М1
при М1→М0 вдоль кривой. Треугол М 0 М 1 А : tgα=AM1/AM0=∆y/∆x=k
M1→M0 отсюда ∆ х →0 α → φ tgα→tgφ
Tgφ=lim(∆x→0)tgα=lim(∆x→0)∆y/∆x=k. Угловым коэф касат назыв предел отношен приращен
фции ∆у к приращ аргумента ∆х при стремлении последнего к 0,если этот предел существует.
Графики:27) 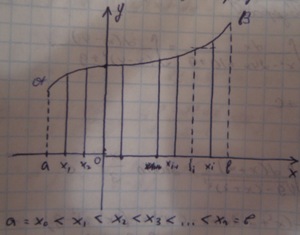
10) 
28)Геометрические приложения определенного интеграла:
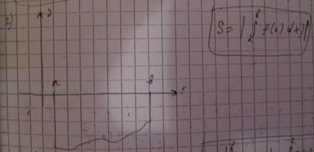
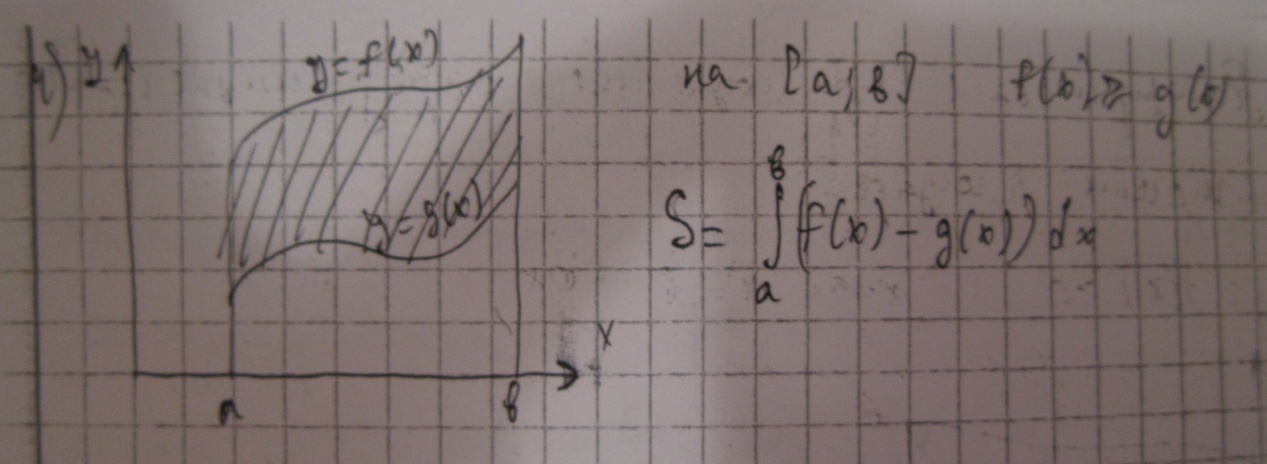
29) для каждого из 4 пунктов сверху вниз по порядку: 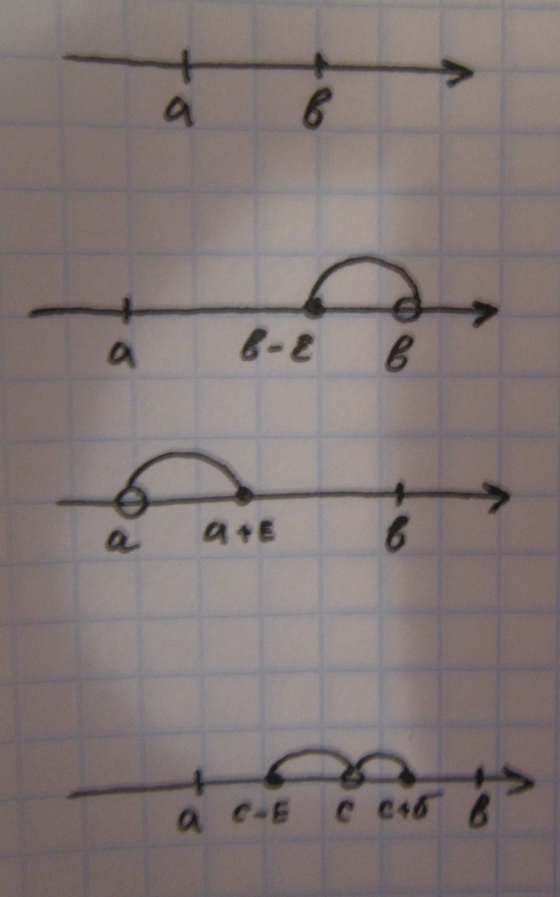
2) 
Расшифровка: ξ-пси; ϕ-фи; lim ( x →0)-предел при икс стремиться к 0.(х→0) при написании сносим под lim ,скобки не пишем.
х0-икс нулевое,0 при написании сносим под х,я практически не сносила числовые индексы после букв вниз,потому что очень мелко,вы сносите обязательно. Т.х-точка икс.








