Лекция от 24.09. Численные методы решения задачи Коши.
Начало темы – метод Эйлера было кратко изложено в конце предыдущей (очной) лекции. Более подробное изложение этого вопроса можно посмотреть в пособии “Дифференциальные уравнения” (файл ДУ_2011.pdf), раздел 1.3, с 21 – 24. Рассмотрим еще два вопроса, которые не охвачены данным пособием.
Оценка точности метода Эйлера.
Оценим сначала ошибку на первом шаге. По формуле Тейлора 1-го порядка с явно выписанным остаточным членом
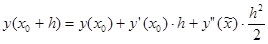, где неизвестная точка 
.
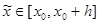Так как, согласно дифференциальному уравнению,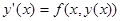 
, справедливо равенство 
.
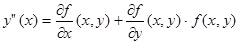Если функция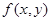 
имеет непрерывные (и значит ограниченные на отрезке) частные производные, то последнее выражение показывает ограниченность функции 
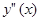, то есть существует такая константа 
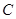, что для любого 
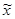из некоторого отрезка правее 
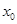выполняется неравенство
.
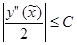Таким образом, для полученной методом Эйлера оценки на первом шаге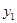 
справедлива оценка погрешности
.
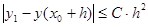Такая же оценка погрешности справедлива и на следующих шагах метода Эйлера.
Пусть решение строится методом Эйлера на отрезке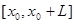 
за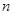 
шагов, тогда шаг 
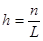. Погрешность в конце отрезка не превосходит суммы погрешностей на каждом шаге, поэтому
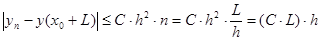
Таким образом, погрешность метода Эйлера для построенного на отрезке решения (при достаточно гладкой функции в правой части уравнения) имеет порядок шага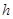 
. Другими словами, число интервалов, на которые нужно разбить отрезок обратно пропорционально допустимой погрешности решения.
Метод Рунге-Кутты.
Метод Эйлера имеет невысокую точность (для высокой точности нужно разбивать отрезок на очень мелкие части) и поэтому в настоящее время обычно используются другие, более точные методы, например, какой-нибудь вариант метода Рунге-Кутты. Простейший (и, соответственно, наименее точный) вариант такого метода - метод Рунге-Кутты 2-го порядка. Этот метод реализуется следующим образом. Как и в методе Эйлера, решение строится с заданным шагом 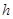, то есть очередное значение аргумента 
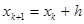. Для получения очередного значения функции строятся две оценки приращения – по оценкам производной в начале и в конце интервала:
,
.
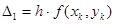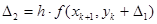Затем используется среднее арифметическое этих приращений:
.
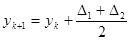Погрешность этого метода для построенного на отрезке решения (при достаточно гладкой функции в правой части уравнения) имеет порядок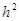 
. Например, для получения решения на заданном отрезке с погрешностью порядка 0.0001 методом Эйлера потребуется сделать около 10000 шагов, а методом Рунге-Кутты 2 порядка – около 100 шагов.