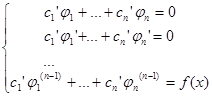Общее решение линейного неоднородного уравнения с постоянными коэффициентами.
Лекция от 15.10.
Общее решение линейного неоднородного уравнения с постоянными коэффициентами.
Теперь речь пойдет о построении общего решения для уравнения вида
.
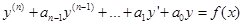Нетрудно убедиться (просто подстановкой в это уравнение), что такое решение может быть представлено в виде суммы
,
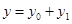где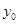 
- общее решение соответствующего однородного уравнения (при 
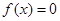), а 
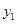- любое конкретное частное решение исходного неоднородного уравнения. Задача построения 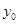была решена на прошлой лекции, остается найти какое-нибудь частное решение .
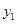Рассмотрим случай, когда правая часть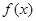 
имеет специальный вид – какая-нибудь линейная комбинацию или произведение полиномов, экспонент, синусов и косинусов. Данные функции обладают тем свойством, что при их дифференцировании получаются функции, подобные исходной. Благодаря этому решение можно искать методом неопределенных коэффициентов, то есть подставляя в уравнение функцию, подобную правой части и содержащую неопределенные коэффициенты, в результате чего получаются уравнения для определения этих коэффициентов.
Если, например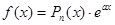 
, где 
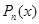- многочлен степени n, то частное решение следует искать в ви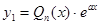де 
, где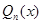 
- многочлен той же степени с неопределенными коэффициентами.
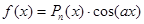Если 
или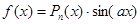 
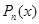, где - многочлен степени n, то частное решение следует искать в виде 
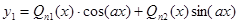, где 
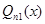и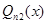 
- два различных многочлена той же степени с неопределенными коэффициентами.
В качестве примера найдем общее решение уравнения
.
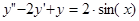Соответствующее однородное уравнение имеет характеристический многочлен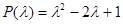 
с кратным корнем 
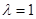, поэтому общее решение однородного уравнения 
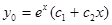. Степень многочлена (множителя при синусе) в правой части n=0, соответственно частное решение следует искать в виде 
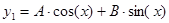, где A и B – неопределенные коэффициенты. Подставив 
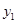в исходное уравнение и приведя подобные члены при синусах и косинусах, получим, что должно выполняться тождество
,
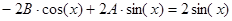откуда следует, что B=0 и A=1. Таким образом,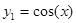 
, и общее решение уравнения 
.
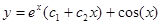Случай резонанса.
Приведенные выше правила формирования частного решения не приведут к успеху, если правая часть уравнения (а значит и подобная ей функция) сама является решением соответствующего однородного уравнения. Этот особый случай называется резонансом. В этом случае правило формирования частного решения следует изменить путем умножения получившегося выражения на x. Убедимся, что это правило работает на примере уравнения 2-го порядка
.
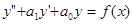Пусть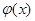 
- содержащая неопределенные коэффициенты функция, подобная правой части, которая одновременно является решением соответствующего однородного уравнения. Подставим в уравнение 
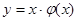. Учитывая, что по правилу дифференцирования произведения 
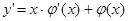и далее 
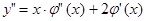, получим
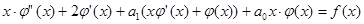, или
.
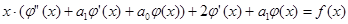Так как 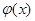является решением соответствующего однородного уравнения, множитель при x тождественно равен нулю, получившееся выражение фактически не содержит x, и получается равенство подобных функций для определения неизвестных коэффициентов для уравнения 2-го порядка в случае резонанса:
. (*)
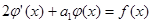Рассмотрим для примера уравнение, описывающее случай классического физического резонанса: частота собственных колебаний системы (решений однородного уравнения) совпадает с частотой внешнего воздействия (правой части)
.
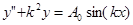Характеристический многочлен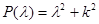 
имеет комплексные корни 
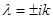, поэтому общее решение однородного уравнения 
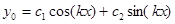и функция, подобная правой части, 
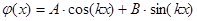является решением однородного уравнения. Таким образом, имеет место случай резонанса, и частное решение следует искать в виде 
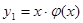. Тогда, согласно равенству (*), так как в нашем случае 
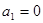, имеем
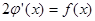, или
.
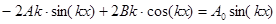Отсюда следует B=0 и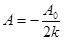 
. Таким образом, частное решение 
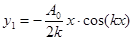и общее решение 
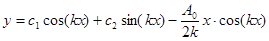, благодаря множителю x, содержит колебания с нарастающей амплитудой.
Метод вариации произвольных постоянных.
Этот универсальный метод применим для любых функций в правой части уравнения, он фактически обобщает ранее изложенный метод решения линейных уравнений 1-го порядка. Рассмотрим этот метод применительно к уравнению 2-го порядка
.
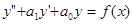Пусть функци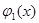и 
и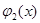 
- линейно независимые решения соответствующего однородного уравнения. Общее решение исходного уравнения будем искать в виде 
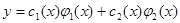(явную запись аргумента x далее будем опускать).
По формуле дифференцирования произведения
.
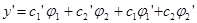Потребуем дополнительно выполнения тождества
.
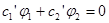Тогда
.
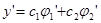
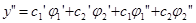Подставив выражение для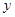 
и его производных в исходное уравнение и учитывая тот факт, что 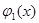и 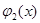являются решениями однородного уравнения, получим равенство
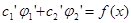
Итак, для определения производных двух неизвестных функци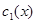й 
и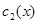 
нужно решить систему из двух линейных уравнений:
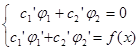
Далее, путем интегрирования получившихся производных, получаются сами функции с добавлением произвольных констант.
Примеры применения этого метода будут разобраны в материалах к практическим занятиям.
В случае уравнения n-го порядка общее решение уравнения ищется в ви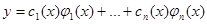де 
, где ,…,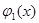 
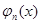- линейно независимые решения соответствующего однородного уравнения, а система для определения производных n неизвестных функций содержит n линейных уравнений:
