Дифференциальные уравнения n -го порядка
Лекция от 08.10.
Дифференциальные уравнения n -го порядка
Дифференциальное уравнение n-го порядка будем записывать в виде
.
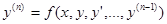Введем n функций:
, 
, …, 
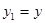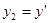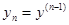
Тогда наше уравнение эквивалентно системе
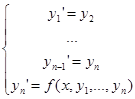
Задачей Коши для исходного уравнения является задача Коши для этой системы, где начальные условия накладываются на все входящие в систему функции. Таким образом, задача Коши для уравнения n-го порядка содержит n начальных условий и может быть записана в виде
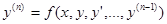
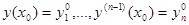
Теорема существования и единственности решения этой задачи Коши является такой теоремой для написанной выше системы (фактически условия накладываются только на функцию правых частей уравнения, поскольку остальные функции очень простые и очевидно всем условиям удовлетворяют).
Отсюда также следует, что запись общего решения уравнения n-го порядка содержит n произвольных констант: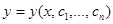 
.
Задача Коши для линейного уравнение n -го порядка с постоянными коэффициентами
Задача Коши для такого уравнения может быть записана в виде
.
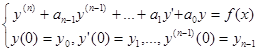Эту задачу можно решить операционным методом, то есть с помощью преобразования Лапласа. Пусть неизвестная функция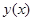 
имеет изображение 
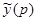. Тогда, согласно свойству дифференцирования оригинала, 
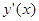имеет изображение 
, 
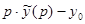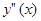, как производная производной, имеет изображение 
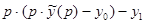, и так далее. В результате после перехода к изображениям дифференциальное уравнение превратится в обычное уравнение относительно неизвестного изображения 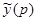. Решив это уравнение и восстановив оригинал по получившемуся изображению, найдем решение задачи Коши.
Общее решение линейного однородного уравнения с постоянными коэффициентами.
Линейное уравнение называется однородным, если его правая часть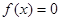 
. Таким образом, линейное однородное уравнение n-го порядка с постоянными коэффициентами имеет вид:
.
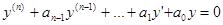Система, эквивалентная этому уравнению, очевидно является линейной однородной (ОСЛДУ), поэтому, согласно Утверждению 2 прошлой лекции это уравнение имеет n линейно независимых решений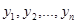 
, а его общее решение может быть записано в виде их линейной комбинации 
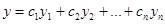(равенство для первых компонент соответствующих вектор-функций).
В частном случае n=1 получается уравнение 1-го порядка с разделяющимися переменными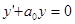 
, у которого, легко найти общее решение 
.
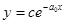В общем случае подставим в уравнение функцию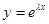 
. Поскольку дифференцирование этой функции эквивалентно умножению на число 
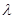, получим:
,
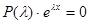где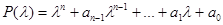 
называется характеристическим многочленом уравнения. Таким образом, функция 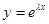является решением нашего уравнения ó число 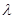является корнем характеристического многочлена. Очевидно, что функции вида 
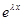являются линейно независимыми при разных значениях 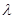. Поэтому в случае, когда многочлен n-й степени 
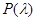имеет n различных вещественных корней 
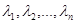, наше уравнение имеет n линейно независимых решений 
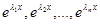, и общее решение уравнения имеет вид
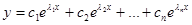
Например, уравнение 2-го порядка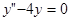 
имеет характеристический многочлен 
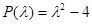с корнями 
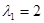и 
, и 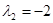его общее решение 
.
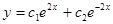Согласно теории многочленов, кратко изложенной в курсе “Алгебра и геометрия” в теме “Комплексные числа”, многочлен n-й степени с вещественными коэффициентами всегда имеет ровно n корней, однако среди них могут быть кратные (повторяющиеся) корни, а также комплексные корни, точнее пары комплексно-сопряженных корней.
Пусть характеристический многочлен 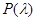имеет комплексно-сопряженные корни 
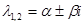. Тогда, соответствующими решениями уравнения будут комплекснозначные функции
,
.
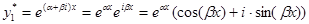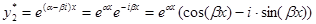(Здесь используется представление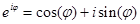 
.)
Из этих решений путем линейных комбинаций нетрудно получить два линейно независимых решения с вещественными значениями
, 
.
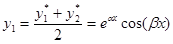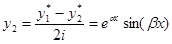Например, уравнение 2-го порядка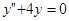 
имеет характеристический многочлен 
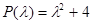с комплексно-сопряженными корнями 
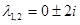, и его общее решение 
.
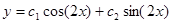Случай кратных корней характеристического многочлена рассмотрим для частного случая уравнения 2-го порядка. Пусть соответствующий характеристический многочлен 2-й степени имеет корень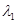 
кратности 2. Тогда он может быть записан в виде
,
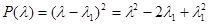и соответствующее ему дифференциальное уравнение имеет вид
.
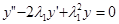Подставим в это уравнение функцию, отличающуюся от уже известного нам решения множителем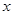 
функцию 
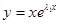. Пользуясь правилом дифференцирования произведения, нетрудно получить выражения для производных этой функции:
, 
.
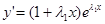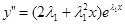Подставив выражения для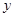 
и его производных в наше уравнение, получим тождество (проверьте самостоятельно). Следовательно, наше уравнение имеет линейно независимые решения 
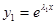и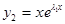 
.
Получившийся факт на самом деле можно обобщить на уравнения любого порядка и корни любой кратности.
Если характеристический многочлен имеет корень 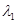кратности k , то соответствующее дифференциальное уравнение имеет k линейно независимых решений вида 
, 
, …, 
.
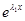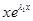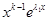Аналогичное утверждение справедливо также для решений, соответствующих кратным комплексно-сопряженным корням.
Итак, найдя все корни (вещественные и комплексные) характеристического многочлена линейного однородного дифференциального уравнения с постоянными коэффициентами, всегда можно получить n линейно независимых решений этого уравнения, и следовательно построить общее решение.