Вероятность попадания в заданный интервал нормальной случайной величины
Как уже было установлено, вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу 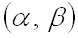 , равна определенному интегралу от плотности распределения, взятому в соответствующих пределах:
, равна определенному интегралу от плотности распределения, взятому в соответствующих пределах: 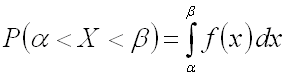
Для нормально распределенной случайной величины соответственно получим: 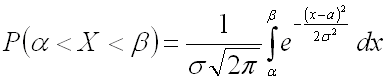
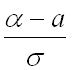 – нижний предел интегрирования;
– нижний предел интегрирования;
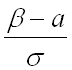 – верхний предел интегрирования;
– верхний предел интегрирования;
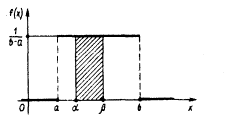
19. Основные свойства и числовые характеристики равномерного закона распределения.
На практике встречаются случайные величины, о которых заранее известно, что они могут принять какое-либо значение в строго определенных границах, причем в этих границах все значения случайной величины имеют одинаковую вероятность (обладают одной и той же плотностью вероятностей).
Определение.
Непрерывная случайная величина Х имеет равномерное распределение на отрезке [а, в], если на этом отрезке плотность распределения вероятности случайной величины постоянна, т. е. если дифференциальная функция распределения f(х) имеет следующий вид:
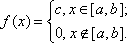
Иногда это распределение называют законом равномерной плотности. Про величину, которая имеет равномерное распределение на некотором отрезке, будем говорить, что она распределена равномерно на этом отрезке.
Найдем значение постоянной с. Так как площадь, ограниченная кривой распределения и осью Ох, равна 1, то
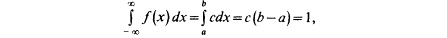 откуда с=1/(b-a).
откуда с=1/(b-a).
Построим функцию распределения F(x), для чего найдем выражение F(x) на интервале [a, b]:
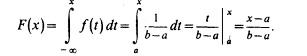
Используя формулу для вычисления математического ожидания НСВ, имеем:
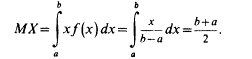
Найдем дисперсию равномерно распределенной случайной величины:
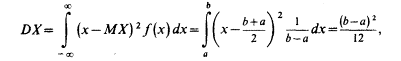
откуда сразу же следует, что среднее квадратическое отклонение:
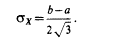
Найдем теперь вероятность попадания значения случайной величины, имеющей равномерное распределение, на интервал (a,b), принадлежащий целиком отрезку [a, b]:
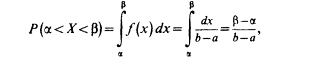
20. Предмет и основные задачи математической статистики. Генеральная и выборочная совокупности.
Математи́ческая стати́стика — наука, разрабатывающая математические методы систематизации и использования статистических данных для научных и практических выводов.
Разработка методов регистрации, описания и анализа статистических экспериментальных данных, получаемых в результате наблюдения массовых случайных явлений, составляет предмет специальной науки – математической статистики.
Все задачи математической статистики касаются вопросов обработки наблюдений над массовыми случайными явлениями, но в зависимости от характера решаемого практического вопроса и от объема имеющегося экспериментального материала эти задачи могут принимать ту или иную форму.
Первая задача математической статистики—указать способы сбора и группировки статистических сведений, полученных в результате наблюдений или в результате специально поставленных экспериментов.
Вторая задача математической статистики—разработать методы анализа статистических данных в зависимости от целей исследования. Сюда относятся:
а) оценка неизвестной вероятности события; оценка неизвестной функции распределения; оценка параметров распределения, вид которого известен; оценка зависимости случайной величины от одной или нескольких случайных величин и др.;
б) проверка статистических гипотез о виде неизвестного распределения или о величине параметров распределения, вид которого известен.
Генеральной совокупностью называют совокупность всех мысленно возможных объектов данного вида, над которыми проводятся наблюдения с целью получения конкретных значений случайной величины, или совокупность результатов всех мыслимых наблюдений, проводимых в неизменных условиях над одной из случайных величин, связанных с данным видом объектов.
Выборочной совокупностью называют часть отобранных объектов из генеральной совокупности.
Объемом совокупности (выборочной или генеральной) называют число объектов этой совокупности. Например, если из 1000 деталей отобрано для обследования 100 деталей, то объем генеральной совокупности N = 1000, а объем выборки п =100.
21. Вариационный, статистический и интервальный статистические ряды.
Статистические ряды распределения являются одним из наиболее важных элементов статистики. Они представляют собой составную часть метода статистических сводок и группировок, но по сути ни одно из статистических исследований невозможно произвести, не представив первоначально полученную в результате статистического наблюдения информацию в виде статистических рядов распределения.
Первичные данные обрабатываются в целях получения обобщенных характеристик изучаемого явления по роду существенных признаков для дальнейшего осуществления анализа и прогнозирования; производится сводка и группировка; статистические данные оформляются с помощью рядов распределения в таблицы, в результате чего информация представляется в наглядном рационально изложенном виде, удобном для использования и дальнейшего исследования; строятся различного рода графики для наиболее наглядного восприятия и анализ информации. На основе статистических рядов распределения вычисляются основные величины статистических исследований: индексы, коэффициенты; абсолютные, относительные, средние величины и т.д., с помощью которых можно проводить прогнозирование, как конечный итог статистических исследований.
Ряд вариационный — статистический ряд чисел в данной выборке или совокупности, состоящий из последовательно расположенных вариант и из частот (повторяемости). Различают простые и сгруппированные вариационные ряды. Требования, предъявляемые к группировке вариационных рядов: размеры интервалов между ними должны соответствовать природе исследуемого явления; желательно, чтобы размеры были тех интервалов, которые должны быть целыми числами или округленными дробями (например, 0,5; 1; 5; 10, но не 0,55; 1,1; 6; 11); границы интервалов должны быть четкими, исключающими попадание одной и той же варианты и разные группы; начало первой группы (класса) должно быть округленным числом (например, 2,0) и не обязательно должно совпадать со значением минимальной варианты (например, 2,2).
Интервальный статистический ряд - это совокупность интервалов вариант и относительных частот попадания их в эти интервалы, нормированных к ширине интервалов. Удобен при построении гистограмм: Отрезок числовой оси, на котором содержатся значения выборки, разбивают на N интервалов шириной x каждый. N=1+3,3lgn (формула Старджеса). Определяют частоту встречаемости значений случайной величины в mi в каждом интервале xi, рассчитывают относительную частоту встречаемости в каждом интервале Pi и делят на ширину интервала xi, величина Pi/ xi приближенно равна dP/dx=f(x). Строят гистограмму, которая является приближенным отображением функции f(x).
22.Графическое представление статистического распределения. Полигон. Гистограмма.
Дли повышения наглядности эмпирических распределений, используется их графическое представление. Наиболее распространенными способами графического представления являются гистограмма, полигон частот и полигон накопленных частот
Гистограмма - один из вариантов столбиковой диаграммы, позволяющий зрительно оценить распределение статистических данных, группированных по частоте попадания в определенный (заранее заданный) интервал.Таким образом, гистограмма представляет собой графическое изображение зависимости частоты попадания элементов выборки от соответствующего интервала значений случайной величины.
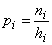 где ni — частота i-го интервала группировки; hi — ширина i-го интервала группировки.
где ni — частота i-го интервала группировки; hi — ширина i-го интервала группировки.
Гистограмма частот (нормальное распределение)
Полигон частот - один из способов графического представления плотности вероятности случайной величины. Представляет собой ломаную, соединяющую точки, соответствующие срединным значениям интервалов группировки и частотам этих интервалов.
Полигон накопленных частот (кумулята) получается при соединении отрезками прямых точек, координаты которых соответствуют верхним границам интервалов группировки и накопленным частотам. Если по оси ординат откладывать накопленные частости, то полученный график называется полигоном накопленных частостей.
23.Числовые характеристики статистического распределения.
Выборочное (эмпирическое) среднее — это приближение теоретического среднего распределения, основанное на выборке из него.
Пусть 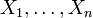 — выборка из распределения вероятности, определённая на некотором вероятностном пространстве
— выборка из распределения вероятности, определённая на некотором вероятностном пространстве 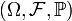 . Тогда её выборочным средним называется случайная величина
. Тогда её выборочным средним называется случайная величина
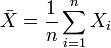 .
.
Выборочная дисперсия в — это оценка теоретической дисперсии распределения на основе выборки. Различают выборочную дисперсию и несмещённую, или исправленную, выборочные дисперсии.
Пусть 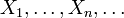 — выборка из распределения вероятности. Тогда
— выборка из распределения вероятности. Тогда
- Выборочная дисперсия — это случайная величина
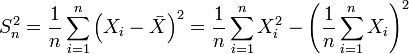 ,
,
где символ 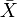 обозначает выборочное среднее.
обозначает выборочное среднее.
- Несмещённая (исправленная) дисперсия — это случайная величина
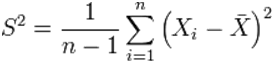
Другими характеристиками вариационного ряда являются:
- мода М0 – варианта, имеющая наибольшую частоту
- медиана те - варианта, которая делит вариационный ряд на две части, равные по числу вариант. Если число вариант нечетно ( n = 2k + 1 ), то me = xk +1, а при четном n =2k
24.Точечные оценки параметров статистического распределения.
Точечная оценка — это число, вычисляемое на основе наблюдений, предположительно близкое к оцениваемому параметру.
Итак, статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин.
Для того чтобы статистические оценки давали «хорошие» приближения оцениваемых параметров, они должны удовлетворять определенным требованиям: оценка должна быть несмещенной, эффективной и состоятельной.
Несмещенной называют статистическую оценку Q*, математическое ожидание которой равно оцениваемому параметру Q при любом объеме выборки, т. е. M(Q*) = Q.
Смещенной называют оценку, математическое ожидание которой не равно оцениваемому параметру.
Эффективной называют статистическую оценку, которая (при заданном объеме выборки п) имеет наименьшую возможную дисперсию.
При рассмотрении выборок большого объема (n велико) к статистическим оценкам предъявляется требование состоятельности.
Состоятельной называют статистическую оценку, которая при п¥® стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при п¥® стремится к нулю, то такая оценка оказывается и состоятельной.
25.Интервальные оценки параметров статистического распределения.
Интервальной называют оценку, которая определяется двумя числами—концами интервала. Интервальные оценки позволяют установить точность и надежность оценок.
Пусть найденная по данным выборки статистическая характеристика Q* служит оценкой неизвестного параметра Q. Будем считать Q постоянным числом (Q может быть и случайной величиной). Ясно, что Q* тем точнее определяет параметр Q, чем меньше абсолютная величина разности |Q- Q*|. Другими словами, если d>0 и |Q- Q*| <d , то чем меньше d , тем оценка точнее. Таким образом, положительное число d характеризует точность оценки. Однако статистические методы не позволяют категорически утверждать, что оценка Q* удовлетворяет неравенству |Q- Q*| <d; можно лишь говорить о вероятности g, с которой это неравенство осуществляется.
Надежностью (доверительной вероятностью) оценки называют вероятность g , с которой осуществляется неравенство |Q—Q* | <d .
Обычно надежность оценки задается наперед, причем в качестве g берут число, близкое к единице. Наиболее часто задают надежность, равную 0,95; 0,99 и 0,999.
Пусть вероятность того, что, |Q- Q*| <d равна g:
P(|Q- Q*| <d)= g.
Заменив неравенство равносильным ему двойным неравенством получим:
Р [Q* —d< Q < Q* +d] = g
Это соотношение следует понимать так: вероятность того, что интервал Q* - d< Q < Q* +d заключает в себе (покрывает) неизвестный параметр Q, равна g.
Интервал (Q* - d Q* +d) называется доверительным интервалом , который покрывает неизвестный параметр с надежностью g.
26.Интервальная оценка математического ожидания нормально распределенной случайной величины.
Нормальное (гауссовское) распределение имеет вид
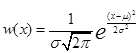
Здесь 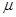 - среднее,
- среднее, 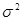 - дисперсия распределения СВ.
- дисперсия распределения СВ.
На рисунке приведен график интегрального гауссовского распределений непрерывной СВ.
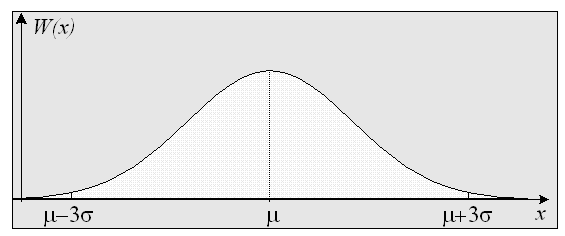
27.Проверка статистических гипотез. Основные понятия.
Статистическая гипотеза — это определённое предположение о распределении вероятностей, лежащем в основе наблюдаемой выборки данных.
Проверка статистической гипотезы — это процесс принятия решения о том, противоречит ли рассматриваемая статистическая гипотеза наблюдаемой выборке данных.
Пусть в (статистическом) эксперименте доступна наблюдению случайная величина 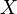 , распределение которой
, распределение которой  неизвестно полностью или частично. Тогда любое утверждение, касающееся
неизвестно полностью или частично. Тогда любое утверждение, касающееся  называется статистической гипотезой. Гипотезы различают по виду предположений, содержащихся в них:
называется статистической гипотезой. Гипотезы различают по виду предположений, содержащихся в них:
1)Статистическая гипотеза, однозначно определяющая распределение 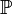 , то есть
, то есть 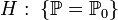 , где
, где 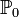 какой-то конкретный закон, называется простой.
какой-то конкретный закон, называется простой.
2)Статистическая гипотеза, утверждающая принадлежность распределения 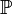 к некоторому семейству распределений, то есть вида
к некоторому семейству распределений, то есть вида 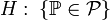 , где
, где 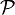 — семейство распределений, называется сложной.
— семейство распределений, называется сложной.
На практике обычно требуется проверить какую-то конкретную и как правило простую гипотезу 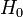 . Такую гипотезу принято называть нулевой. При этом параллельно рассматривается противоречащая ей гипотеза
. Такую гипотезу принято называть нулевой. При этом параллельно рассматривается противоречащая ей гипотеза 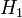 , называемая конкурирующей или альтернативной.
, называемая конкурирующей или альтернативной.
Выдвинутая гипотеза нуждается в проверке, которая осуществляется статистическими методами, поэтому гипотезу называют статистической. Для проверки гипотезы используют критерии, позволяющие принять или опровергнуть гипотезу.
В результате проверки правильности выдвинутой нулевой гипотезы ( такая проверка называется статистической, так как производится с применением методов математической статистики) возможны ошибки двух видов: ошибка первого рода, состоящая в том, что будет отвергнута правильная нулевая гипотеза, и ошибка второго рода, заключающаяся в том, что будет принята неверная гипотеза.
27. Общая методика проверки статистических гипотез.
Этапы проверки статистических гипотез
- Формулировка основной гипотезы
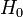 и конкурирующей гипотезы
и конкурирующей гипотезы 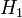 . Гипотезы должны быть чётко формализованы в математических терминах.
. Гипотезы должны быть чётко формализованы в математических терминах. - Задание уровня значимости
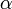 , на котором в дальнейшем и будет сделан вывод о справедливости гипотезы. Он равен вероятности допустить ошибку первого рода.
, на котором в дальнейшем и будет сделан вывод о справедливости гипотезы. Он равен вероятности допустить ошибку первого рода. - Расчёт статистики
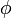 критерия такой, что:
критерия такой, что: - её величина зависит от исходной выборки
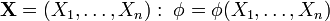 ;
; - по её значению можно делать выводы об истинности гипотезы
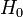 ;
; - сама статистика
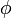 должна подчиняться какому-то известному закону распределения, так как сама
должна подчиняться какому-то известному закону распределения, так как сама 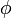 является случайной в силу случайности
является случайной в силу случайности 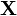 .
. - Построение критической области. Из области значений
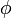 выделяется подмножество
выделяется подмножество 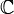 таких значений, по которым можно судить о существенных расхождениях с предположением. Его размер выбирается таким образом, чтобы выполнялось равенство
таких значений, по которым можно судить о существенных расхождениях с предположением. Его размер выбирается таким образом, чтобы выполнялось равенство 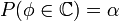 . Это множество
. Это множество 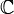 и называется критической областью.
и называется критической областью. - Вывод об истинности гипотезы. Наблюдаемые значения выборки подставляются в статистику
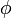 и по попаданию (или непопаданию) в критическую область
и по попаданию (или непопаданию) в критическую область 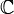 выносится решение об отвержении (или принятии) выдвинутой гипотезы
выносится решение об отвержении (или принятии) выдвинутой гипотезы 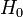 .
.
29. Проверка гипотез о значениях математического ожидания нормальной случайной величины.
Пусть имеется выборка n значений нормально распределенной случайной величины: х1, х2, ..., xn. Требуется проверить гипотезу о том, что математическое ожидание х равно определенному значению (обозначим его a).
Итак гипотеза Н0: Мх = a.
В качестве критерия выбираем случайную величину
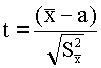
закон распределения которой нам известен .
Очевидно, гипотезу следует отвергнуть и в том случае, если среднее арифметическое много больше а, и в том случае, если среднее арифметическое много меньше а, поэтому критическая область будет двухсторонней, т.е. Q: | t | > tq, так, чтобы Р (| t | ;> tq / H0) = α. По выбранному α и таблице t-распределения находим tq при ν = n - 1; вычисляем 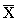 ,
, 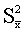 , и tэ по данным эксперимента и принимаем гипотезу, если | tэ | < tq, в противном случае - отвергаем.
, и tэ по данным эксперимента и принимаем гипотезу, если | tэ | < tq, в противном случае - отвергаем.
30. Проверка гипотезы о значениях дисперсии нормальной случайной величины.
Для проверки гипотезы 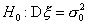 о равенстве дисперсии
о равенстве дисперсии 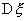 нормально распределенной случайной величины
нормально распределенной случайной величины 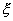 заданному числу
заданному числу 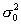 рекомендуется использовать статистику
рекомендуется использовать статистику
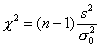
Можно показать, что эта статистика при условии, что верна гипотеза H0, распределена по закону c2 с п-1 степенями свободы. Критическая область уровня 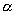 при двусторонней альтернативе
при двусторонней альтернативе 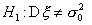 состоит из двух промежутков:
состоит из двух промежутков: 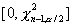 и
и 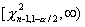 , где
, где 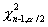 и
и 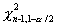 - квантили порядка
- квантили порядка 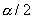 и
и 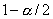 распределения
распределения 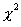 с п-1 степенями свободы. Для односторонней альтернативы
с п-1 степенями свободы. Для односторонней альтернативы 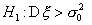 критическая область имеет вид
критическая область имеет вид 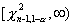 , а для альтернативы
, а для альтернативы 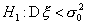 - соответственно,
- соответственно, 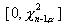 .
.








