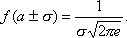Свойства геометрического распределения
· Из всех дискретных распределений с фиксированным средним геометрическое распределение является одним из распределений с максимальной информационной энтропией.
· Геометрическое распределение бесконечно делимо.
(Пусть производятся независимые испытания, в каждом из которых вероятность появления события А равна р (О < р < 1) и, следовательно, вероятность его не появления q = 1 - р. Испытания заканчиваются, как только появится событие А (т.е. количество испытаний неограниченно). Таким образом, если событие А появилось в k-м испытании, то в предшествующих k—1 испытаниях оно не появлялось.)
15. Основные свойства и числовые характеристики случайной величины, распределенной по гипергеометрическому закону.
Гипергеометрическое распределение. Дискретная случайная величина Х имеет гипергеометрическое распределение с параметрами a, b, n, если ее возможные значения 0, 1, 2, ... , m, … , а имеют вероятности:
P ( X = m ) =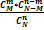 
Мат.ожидание: M(X)=n* 
Дисперсия: D(X)=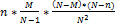 
(N – общее количество изделий, М – особо колич. Изделий(стандартных))
Гипергеометрическое распределение возникает, например, когда из урны, содержащей а черных и b белых шаров, вынимают n шаров. Случайной величиной, подчиненной гипергеометрическому закону распределения, является число белых шаров среди вынутых.
16. Основные свойства и числовые характеристики показательного закона распределения.
Экспоненциальное или показательное распределение — абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события.
Функция распределения: Fx ( x ) =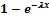 
Мат.ож.: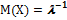 
Дисперсия: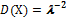 
Мода: 0
Плотность вер.: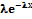 
Свойства:
· Плотность вероятности определена почти всюду. Если f является плотностью вероятности P и f ( x ) = g ( x ) почти всюду относительно меры Лебега, то и функция g также является плотностью вероятности P.
· Интеграл от плотности по всему пространству равен единице:
Обратно, если f ( x ) — неотрицательная п.в. функция, такая что
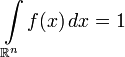, то существует абсолютно непрерывная вероятностная мера P на Rn такая, что является её плотностью.
· Замена меры в интеграле Лебега:
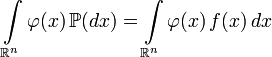
где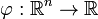 
любая борелевская функция, интегрируемая относительно вероятностной меры .
17. Основные свойства и числовые характеристики нормального закона распределения.
Нормальное распределение, также называемое гауссовым распределением или распределением Гаусса — распределение вероятностей, которое задается функцией плотности распределения:
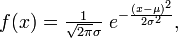где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ² — дисперсия.
Свойства:
Если случайные величины X1 и X2 независимы и имеют нормальное распределение с математическими ожиданиями m1 и m2 и дисперсиями σ²1 и σ² 2 соответственно, то также имеет нормальное распределение с математическим ожиданием m1 + m2 и дисперсией σ²1 + σ² 2.
Числовые характеристики:
μ — среднее значение (математическое ожидание)
σ² — дисперсия
мода = медиана — μ
18. Вероятность попадания случайной величины на заданный интервал для нормального закона распределения. Функции Лаппласа, ее свойства.
Преобразова́ние Лапла́са — интегральное преобразование, связывающее функцию комплексного переменного (изображение) с функцией вещественного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.
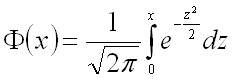Дисперсия: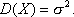 
свойства функции:
1. Областью определения функции f(x) является вся числовая ось.
2. Функция f{x) может принимать только положительные значения, т. е. f(x}>0.
3. Предел функции f(x) при неограниченном возрастании |х| равен нулю, т. е. ось ОХ является горизонтальной асимптотой графика функции.
4. Функция f{x) имеет в точке х = a максимум, равный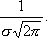 
5. График функции f(x) симметричен относительно прямой х = а.
6. Нормальная кривая в точках х = а +s имеет перегиб, 