Вероятностный смысл математического ожидания

Дата: 2025-05-01; Просмотры: 4

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины (тем точнее, чем больше число испытаний).

Свойства математического ожидания:

1. Математическое ожидание постоянной величины равно самой постоянной: М(С)=С

2. Постоянный множитель можно выносить за знак математического ожидания: М(С*Х)=С*М(Х)

3. 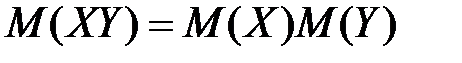Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:

4. Математическое ожидание суммы двух случайных величин (зависимых или независимых) ровно сумме математических ожиданий слагаемых:

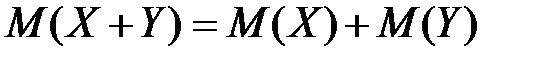
10. Дисперсия и среднеквадратическое отклонение случайной величины. Свойства дисперсия.

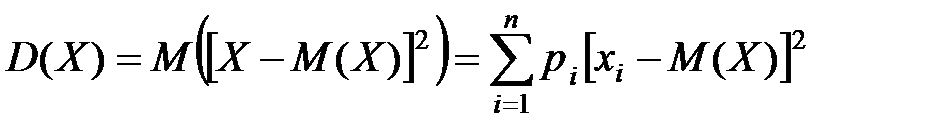Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

Для непрерывной СВ имеем

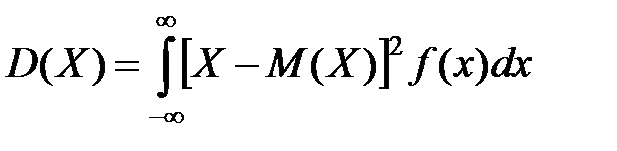
Замечание.Из определения следует, что дисперсия СВ есть неслучайная (постоянная) величина.

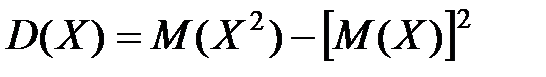Теорема.Дисперсия равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания:

Свойства дисперсии

1. Дисперсия постоянной величины С равна нулю: D( c )=0

2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: D(C*X)=C²*D(X)

3. 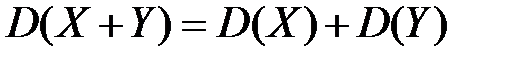Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:

C ледствия:

1. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин.

2. Дисперсия суммы постоянной величины и случайной равна дисперсии случайной величины.

3. 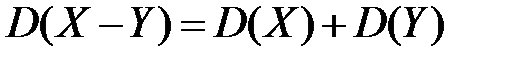Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:

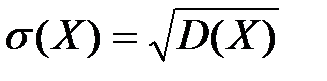Средним квадратичным отклонением (СКО) случайной величины X называют квадратный корень из дисперсии:

Дисперсия имеет размерность, равную квадрату размерности случайной величины.

Размерность СКО совпадает с размерностью СВ X.

11. Мода, медиана, начальные и центральные теоретические моменты.

Мода (Дискретной Случайной Величины) «Х» называют её значение, принимаемое с наибольшей вероятностью по сравнению с другими

М₀(х)=М₀Х

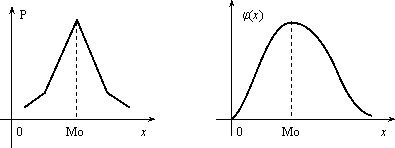
Модой дискретной случайной величины, обозначаемой Мо, называется ее наиболее вероятное значение (рис.1),
а модой непрерывной случайной величины – значение, при котором плотность вероятности максимальна (рис.2)

Медианой непрерывной случайной величины Х называется такое ее значение Ме, для которого одинаково вероятно, окажется ли случайная величина меньше или больше Ме, т.е.

Р(Х < Ме) = Р(X > Ме)

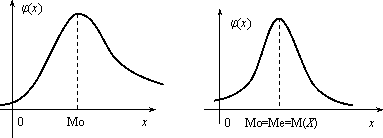
Из определения медианы следует, что Р(Х<Ме) = 0,5, т.е. F (Ме) = 0,5. Геометрически медиану можно истолковывать как абсциссу, в которой ордината φ(x) делит пополам площадь, ограниченную кривой распределения (рис.1). В случае симметричного распределения медиана совпадает с модой и математическим ожиданием (рис.2).

Начальным моментом k-го порядка αk случайной величины Х называется математическое ожидание величины Х ^k, т.е. αk = М(Хk).

( Начальный момент первого порядка – это математическое ожидание случайной величины)

Центральным моментом k-го порядка μk случайной величины Х называется математическое ожидание величины (Х–М(Х)) ^k, т.е. μk = М(Х–М(Х))k.

(Центральный момент второго порядка – это дисперсия случайной величины)

12. Основные свойства и числовые характеристики случайной величины, распределенной по Биномиальному закону.

Биномиа́льное распределе́ние в теории вероятностей — распределение количества «успехов» в последовательности из независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них постоянна и равна p.

Формула: P_n ( k ) = C_n^k · p^k · q^{n - k}

Числовые характеристики случайной величины, распределенной по биномиальному закону

Закон распределения полностью характеризует случайную величину с вероятностной точки зрения. Зная закон распределения случайной величины, можно указать, где располагаются возможные значения случайной величины и какова вероятность ее появления в том или ином интервале.

1. Теорема: «Математическое ожидание M(X) биномиального распределения числа появлений события А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании»
(то есть M(X)=np)

2. Теорема: «Дисперсия биномиального распределения числа появлений события А в n независимых испытаниях, в каждом из которых вероятность p появления события постоянна, равна произведению числа испытаний n на вероятности появления и не появления события в одном испытании»
(то есть D(X) = npq)

3. Теорема: «Среднее квадратическое отклонение суммы конечного числа взаимно независимых случайных величин равно квадратическому корню из суммы квадратов средних квадратических отклонений этих величин»
( s (Х) = 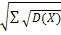или s (Х) =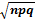

___________________

Пусть в каждом из n независимых испытаний событие А может произойти с одной и той же вероятностью р (следовательно, вероятность непоявления q =1 – p). Дискретная случайная величина Х – число наступлений события А – имеет распределение, которое называется биномиальным.

Очевидно, событие А в n испытаниях может либо не появиться, либо появиться 1 раз, либо 2 раза, …, либо n раз. Таким образом, возможные значения Х таковы: х1 = 0, х2 = 1, х3 = 2,…, хn+1 = n. Вероятность возможного значения Х = k (числа k появления события) вычисляют по формуле Бернулли:

P_n ( k ) = C_n^k · p^k · q^{n - k} , где k = 0, 1, 2, …, n.

Св-ва: 1)Пусть 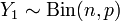и 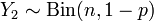. Тогда .

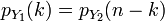2)Пусть 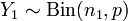и 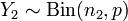. Тогда .

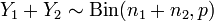13. Основные свойства и числовые характеристики случайной величины, распределенной по закону Пуассона.

Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.
Формула: P_n ( k ) =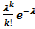

Отличительная особенность данного распределения состоит в том, что математическое ожидание и дисперсия равны параметру распределения

т.е. М(Х)= np =D(X).
Тогда среднее квадратическое отклонение равно s (Х) =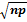

Свойства:

· Сумма независимых пуассоновских случайных величин также имеет распределение Пуассона. Пусть 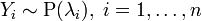. Тогда

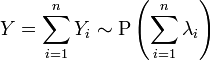
· Пусть 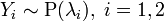, и 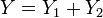. Тогда условное распределение при условии, что , биномиально. Более точно:

____________

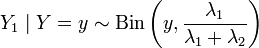
Это распределение представляет собой предельный случай биномиального, когда вероятность р очень мала, а число испытаний n велико.

Таким образом, им можно пользоваться при описании частот распределения редких событий, таких, например, как случай обширных наводнений на протяжении долгого периода времени наблюдений.

Дискретная случайная величина Х, которая может принимать только целые неотрицательные значения с вероятностями P_n ( k ) =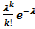

где k – число появления событий в n независимых испытаниях, λ = n · p (среднее число появлений события в n испытаниях), называется распределенной по закону Пуассона с параметром λ .

В отличие от биномиального распределения здесь случайная величина может принимать бесконечное множество значений, представляющее собой бесконечную последовательность целых чисел 0, 1, 2, 3, … .

Закон Пуассона описывает число событий k , происходящих за одинаковые промежутки времени. При этом полагается, что события появляются независимо друг от друга с постоянной средней интенсивностью, которая характеризуется параметром λ = n · p . Так как для распределения Пуассона вероятность р появления события в каждом испытании мала, то это распределение называют законом распределения редких явлений.

По распределению Пуассона распределено, например число посетителей магазина или банка за определенный промежуток времени, при этом λ – среднее число посетителей за это время

14. Основные свойства и числовые характеристики случайной величины, распределенной по геометрическому закону.

Геометри́ческое распределе́ние в теории вероятностей — распределение дискретной случайной величины равной количеству испытаний случайного эксперимента до наблюдения первого «успеха».

Формула: P ( X = k ) =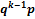

(Обозначим через X дискретную случайную величину - число испытаний, которые нужно провести до первого появления события А. Очевидно, возможными значениями Х являются натуральные числа: 1, 2, 3…)

Мат.Ожидание: M ( X ) =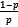

Дисперсия: D ( X ) =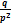

Мода: 0