Закон распределения случайной величины.
Законом распределения дискретной случайной величины называют соответствие между её возможными значениями и их вероятностями.
Закон распределения можно задать:
} таблично,
} аналитически (в виде формулы),
} графически.
При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая ‑ их вероятности.
По определению в одном испытании случайная величина принимает одно и только одно возможное значение, а значит события X=x1, X=x2, X=xn
Образуют полную группу событий, и следовательно
P(X=x1)+P( X=x2)+P( X=xn)=p1+p2+…pn=1
7. Функция распределения случайной величины, ее свойства.
Непрерывная СВ не может быть задана с помощь закона распределения (невозможно указать все значения НСВ).
Функцией распределения называют функцию F(х), определяющую вероятность того, что случайная величина X в результате испытания примет значение, меньшее х, т. е.
F(x)=p(X<x)
Свойства функции распределения
1. Значения функции распределения принадлежат отрезку [0, 1] (как вероятность по определению): 0<=F(x)<=1
2. Функции распределения - неубывающая функция, т. е. F(x2)>=F(x1), если х2>=x1
3. Если возможные значения случайной величины принадлежат интервалу ( a , b ) , то:
1) F(x)=0 при x<=a
2) F(x)=1 при X>=b
C ледствия:
1. Вероятность того, что случайная величина примет значение, заключенное в интервале ( a , b ) , равна приращению функции распределения на этом интервале: P(a<=X<=b)=F(b)-F(a)
2. Вероятность того, что непрерывная случайная величина X примет одно определенное значение, равна нулю.
3. Если возможные значения непрерывной случайной величины расположены на всей оси Ox, то справедливы следующие предельные соотношения:
1) limF(x)=0 (x->бесконечность)
2) limF(x)=1 (x->бесконечность)
8. Плотность распределения вероятностей непрерывной случайной величины. Свойства плотности вероятностей.
Плотностью распределения вероятностей непрерывной случайной величины X называют функцию f ( x ) – первую производную от функции распределения F ( x ) : f(x)= F’(x)
Замечание. Плотность распределения вероятностей неприменима для описания дискретных случайных величин
Свойства плотности вероятностей f ( x )
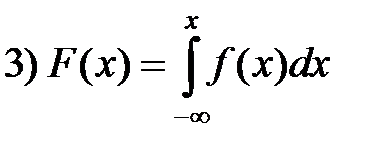
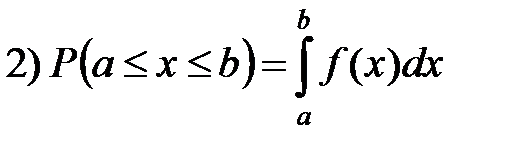
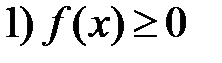
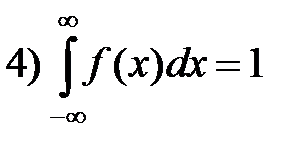
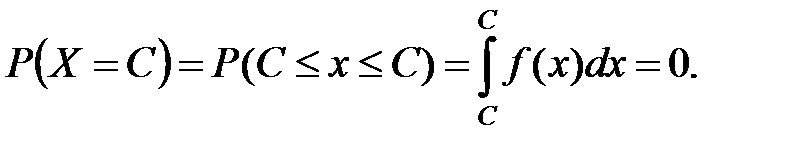 Замечание.Для непрерывной случайной величины имеем:
Замечание.Для непрерывной случайной величины имеем:
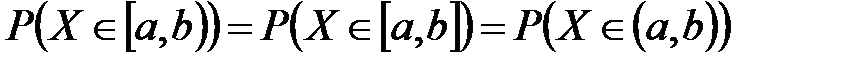 Т.е. вероятность того, что НСВ примет какое-то конкретное значение С равна нулю.
Т.е. вероятность того, что НСВ примет какое-то конкретное значение С равна нулю.
Откуда следует:
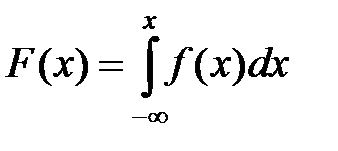 Случайную величину X называют непрерывной , если существует неотрицательная функция f ( x) , такая, что при любых x функцию распределения F ( x ) можно представить в виде
Случайную величину X называют непрерывной , если существует неотрицательная функция f ( x) , такая, что при любых x функцию распределения F ( x ) можно представить в виде
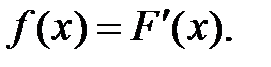
а затем получить, что
9. Математическое ожидание случайной величины. Свойства математического ожидания.
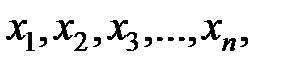 Математическим ожиданием ДСВ X называют сумму произведений всех ее возможных значений на их вероятности.
Математическим ожиданием ДСВ X называют сумму произведений всех ее возможных значений на их вероятности.
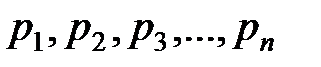 Пусть ДСВ X может принимать значения
Пусть ДСВ X может принимать значения
вероятности которых соответственно равны
Тогда математическое ожидание M ( X ) случайной величины X определяется равенством:
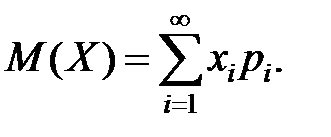 М(Х)=х1*р1+х2*р2+х3*р3+…+хп*рп
М(Х)=х1*р1+х2*р2+х3*р3+…+хп*рп
или
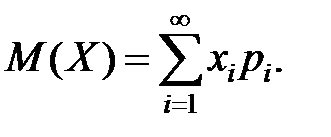
Если число значений ДСВ бесконечно, то
Для непрерывной случайной величины имеем :
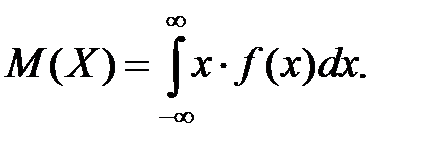
Замечание
Из определения следует, что математическое ожидание случайной величины есть неслучайная (постоянная) величина.








