Просмотреть видеоурок и презентацию к уроку, составить краткий конспект урока.
а) Работа по формированию понятия о правильных многогранниках.
Мне хотелось бы начать со слов Бертрана Рассела: “Математика владеет не только истиной, но и высшей красотой - красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства”.
Название “правильные” идет от античных времен, когда стремились найти гармонию, правильность, совершенство в природе и человеке. Так вот, оказывается, среди всех многогранников существуют особые многогранники, которые называются правильными. Давайте попробуем вместе сформулировать определение правильного многогранника, сравнивая их с другими многогранниками. Правильные многогранники – это многогранники, у которых все грани являются правильными многоугольниками и они равны.
Частично–поисковая работа (определение видов правильных многогранников).
Много ли существует видов правильных многогранников? Как установить количество видов правильных многогранников? (Все грани – правильные многоугольники; все многогранные углы должны быть равны, в каждую вершину должно сходиться одинаковое число ребер, граней, значит нужно установить, сколько граней может сходиться в одну вершину; должен существовать многогранный угол правильного многогранника, условие существования – сумма всех его плоских углов nα меньше 360°).
Существует 5 видов правильных многогранников: тетраэдр, гексаэдр, октаэдр, додекаэдр, икосаэдр.


Почему правильные многогранники получили такие имена?
Это связано с числом их граней. В переводе с греческого языка: эдрон – грань, тетра – четыре, гекса – шесть, окто – восемь, додека – двенадцать, икоси – двадцать.
Все правильные многогранники были известны еще в Древней Греции, и им посвящена заключительная, 13-я книга знаменитых “Начал” Евклида.
Правильные многогранники иногда называют Платоновыми телами, поскольку они занимают видное место в философской картине мира, разработанной великим мыслителем Древней Греции Платоном (ок. 428 – ок. 348 до н.э.). Платон считал, что мир строится из четырёх «стихий» - огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырёх правильных многогранников.
Тетраэдр олицетворял огонь, поскольку его вершина устремлена вверх, как у разгоревшегося пламени; икосаэдр – как самый обтекаемый – воду; куб – самая устойчивая из фигур – землю, а октаэдр – воздух.
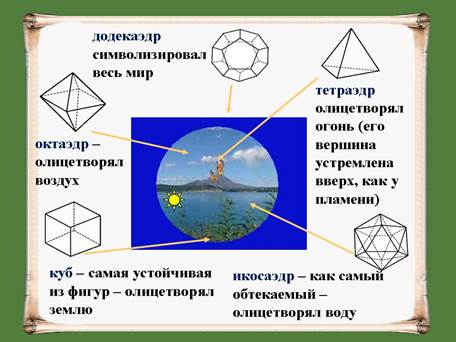
В наше время эту систему можно сравнить с четырьмя состояниями вещества - твёрдым, жидким, газообразным и пламенным. Пятый многогранник – додекаэдр символизировал все мироздание и почитался главнейшим– его по-латыни стали называть quinta essentia (квинта эссенция), означающее все самое главное, основное, истинную сущность чего-либо. Это была одна из первых попыток ввести в науку идею систематизации.
Правильные многогранники встречаются в живой природе. Например, скелет одноклеточного организма феодарии по форме напоминает икосаэдр. Большинство феодарий живут на морской глубине и служат добычей коралловых рыбок. Но простейшее животное пытается себя защитить: из 12 вершин скелета выходят 12 полых игл. На концах игл находятся зубцы, делающие иглу еще более эффективной при защите. Из всех многогранников с тем же числом граней именно икосаэдр имеет наибольший объем при наименьшей площади поверхности. Это свойство помогает морскому организму преодолевать давление водной толщи.
Интересно, что икосаэдр оказался в центре внимания биологов в их спорах относительно формы некоторых вирусов. Вирус не может быть совершенно круглым, как считалось раньше. Для того чтобы определить его форму, брали разные многогранники, направляли на них свет под теми же углами, что и поток атомов на вирус. Оказалось, что только один многогранник дает точно такую же тень – икосаэдр. Головка вируса-бактериофага также имеет форму икосаэдра. Вирус полиомиелита имеет форму додекаэдра. Он может жить и размножаться только в клетках человека и приматов.
Природа широко пользуется тем, что правильные многогранники – самые выгодные фигуры. Это подтверждают формы некоторых кристаллов. Кристаллическая решётка метана имеет форму тетраэдра. Метан горит бесцветным пламенем. С воздухом образует взрывоопасные смеси. Используется как топливо.
Кристаллическая решетка поваренной соли. Маленькие шарики – ионы натрия, большие – ионы хлора. Все кристаллы поваренной соли имеют одинаковую кубическую форму.
Пирит. Пирит обычно образует зернистые массы среди других сульфидных минералов. Часто представлен кристаллами в виде кубов, на гранях которых почти всегда наблюдается характерная штриховка. Окрас – желтый с разными оттенками. Окраска и определила название – «пирос» (по-гречески значит «огонь»). Сырье для получения серной кислоты; руда золота, меди, кобальта.
Магнетит. Обычно встречается в виде мелких зерен, но может образовывать октаэдрические кристаллы. Железо-черные кристаллы, зернистые массы. Встречается в кварцитах и кристаллических сланцах. Главная руда железо.
Алмаз. Кристаллы алмаза обычно имеют форму октаэдра. Алмаз (от греческого adamas – несокрушимый) – бесцветный или окрашенный кристалл с сильным блеском в виде октаэдра. Кристаллы алмаза представляют собой гигантские полимерные молекулы и обычно имеют форму октаэдров, реже — кубов или тетраэдров. Широко используется в ювелирном деле.
б) Исследовательская работа. Проблема:
Цель: Выявить зависимость между числами вершин, граней и ребер выпуклого многогранника.
Гипотеза: Если существует зависимость между числами вершин, граней и ребер, то ее можно выразить формулой и по ней найти число ребер выпуклого многогранника.
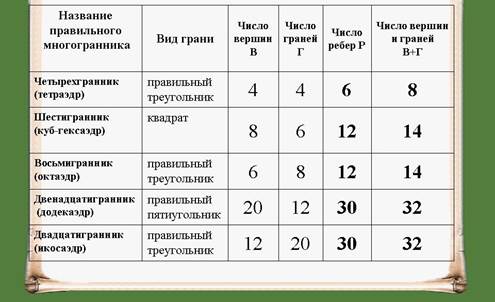
ТЕОРЕМА ДЕКАРТА-ЭЙЛЕРА: В любом выпуклом многограннике сумма числа граней и числа вершин больше числа ребер на 2. (Вершины+Грани – Ребра = 2).
Итог урока.
Итак, многогранники – это не выдумка учёных, не абстракция, они окружают нас в жизни, в природе, в искусстве. Их изучали учёные и древности, и средних веков, но идеи Пифагора и Платона оказались удивительного современными – это были первые попытки систематизации окружающего нас мира. Гениальное предвидение Пифагора о том, что математика откроет человечеству двери к тайне Мироздания, сбылись, хотя ждать пришлось более 2-х тысячелетий. Таким образом, на каком же уроке мы с вами побывали? Алгебры? Геометрии? А мы нашли точки соприкосновения со множеством предметов и явлений, и в этом великая сила и тайна математики.
Задание на дом: учебник «Геометрия 10-11» авт. Л.С. Атанасян, 2014г., глава 3, §1, стр. 60, составить краткий конспект урока (начертить таблицу «Правильные многогранники») и изготовить модель правильного многогранника.








