Пределом разрешения микроскопа называется наименьшее расстояние между двумя точками объекта, когда эти точки различимы, т.е. воспринимаются в микроскопе не сливающимися друг с другом.
Предел разрешения определяется формулой δ=0,51·λ/A, величина А=n·sinu называется числовой апертурой микроскопа; λ - длина волны света, освещающего предмет; n - показатель преломления среды между объективом и предметом; u - апертурный угол объектива, равный половине угла между крайними лучами конического светового пучка, входящего в объектив микроскопа.
Данные о каждом объективе маркируются на его корпусе с указанием следующих параметров):
1) увеличение («х» – кратность, размер);
2) числовая апертура: 0,20; 0,65, пример: 40/0,65 или 40х/0,65;
3) дополнительная буквенная маркировка, если объектив используется при различных методах исследования и контрастирования: фазовый – Ф, поляризационный – П (Pol), люминесцентный – Л (L), и т.п.
4) маркировка типа оптической коррекции: апохромат – АПО (АРО), планахромат – ПЛАН (PL, Plan),.
Разрешающей способностью микроскопа называется способность микроскопа давать раздельное изображение мелких деталей предмета. Разрешающая способность - это величина, обратная пределу разрешения ξ = 1/δ.
Как видно из формулы, разрешающая способность микроскопа зависит от его технических параметров, но физический предел этого параметра определяется длиной волны падающего света.
Повысить разрешающую способность микроскопа можно, заполнив пространство между предметом и объективом иммерсионной жидкостью с большим показателем преломления.
Глубиной резкости называется расстояние от самой ближней плоскости до самой дальней плоскости объекта, которые изображаются приемлемо сфокусированными.
Если точки предмета находятся на различных расстояниях перед объективом (в разных плоскостях), то формируемые им резкие изображения этих точек будут находиться также на различных расстояниях позади объектива. Это должно означать, что резкие изображения могут быть образованы только точками, лежащими в одной плоскости. Остальные точки в этой плоскости будут отображаться кружками, которые называются кружками рассеяния. (рис.2).
| Рис.2.Зависимость резкости изображения от расстояния между предметами и объективом. A, B, C — точки равноудалённых предметов. A1, B1, C1 — точки пересечения лучей, прошедших через линзу. |
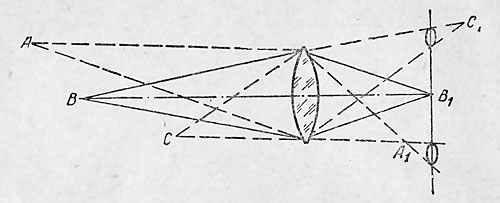
Величина кружка зависит от расстояния от данной точки до плоскости отображения. Вследствие ограниченной разрешающей способности глаза точки, отображаемые малыми кружками, будут восприниматься как точки и соответствующая плоскость объекта будет рассматриваться как сфокусированная. Глубина резкости тем больше, чем короче фокусное расстояние объектива, чем меньше диаметр действующего отверстия (диаметр оправы линзы или отверстия диафрагмы). На рис.2.показана зависимость глубины резкости от перечисленных факторов. При прочих равных условиях, то есть при F постоянном и также постоянном расстоянии от объектива до объекта, для увеличения глубины резкости уменьшают диаметр действующего отверстия. С этой целью между линзами объектива устанавливается диафрагма, позволяющая изменить диаметр входного отверстия.
Поле зрения оптической системы - часть пространства (плоскости), изображаемая этой системой. Величина поля зрения определяется входящими в систему деталями (такими как оправы линз, призм и зеркал, диафрагмы и пр.), которые ограничивают пучок лучей света.
6. Измерения геометрических размеров объекта с помощью оптического микроскопа
Для измерения геометрических размеров в микроскопах используют окуляр-микрометр и винтовой окуляр-микрометр. Окуляр-микрометр представляет собой окуляр с мерной шкалой. Изображение объектов под микроскопом измеряется окуляр-микрометром в делениях его шкалы. Поворотом окуляра, в который вложен окуляр-микрометр, и перемещением препаратоводителя на столике микроскопа, совмещают шкалу окуляр-микрометра с измеряемым объектом по направлению измерения. Определяют количество делений окуляр-микрометра, приходящееся на длину (ширину) объекта.
| Рис.3. Винтовой окуляр-микрометр: а- внешний вид; б – шкала и подвижная сетка с перекрестием в поле зрения окулярного микрометра |
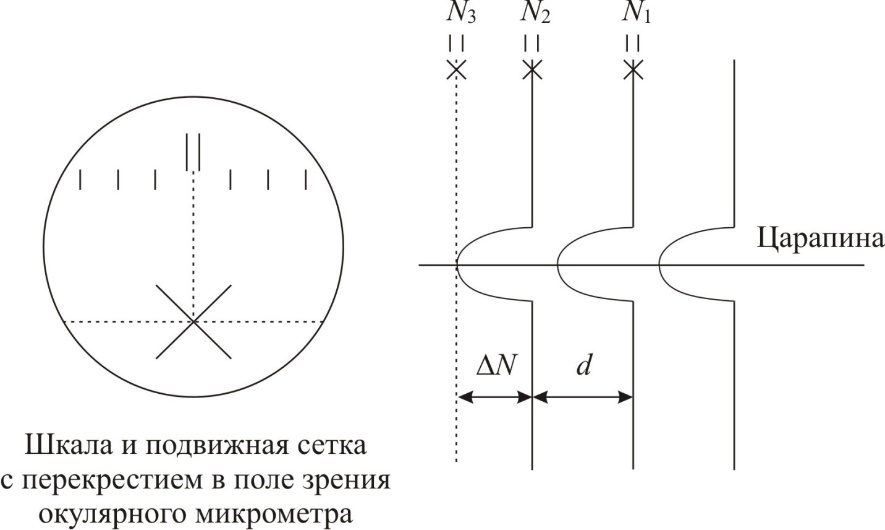
Винтовой окуляр-микрометр представляет собой сочетание микрометрической шкалы с микрометрической винтовой парой. Внешний вид показан на рис.3а. В фокальной плоскости окулярного микрометра расположена неподвижная шкала из 8 делений. В этой же плоскости расположено подвижное перекрестие с жестко связанным с ним указателем - двойной риской (см. рис.3б).
Наблюдая в окуляр и вращая барабан по часовой стрелке, подводят центр перекрестия до совмещения с краем измеряемого объекта и делают первый отсчет по шкалам окуляр-микрометра по положению рисок. При вращении винта перекрестие перемещается в поле зрения по изображению объекта, а двойная риска одновременно движется по шкале целых делений. Поверхность барабана разделена на 100 делений, соответственно, поворот барабана на одно такое деление перемещает перекрестие на 0,01 от деления шкалы, видимой в окуляре. Полный отсчёт окулярного микрометра, складывается из отсчётов целых по шкале в окуляре и сотых по барабану винта. По шкале в поле зрения отсчитывают полные мм, а по шкале барабана - сотые доли мм. Таким образом подводят перекрестие до совмещения его центра с изображением второго края измеряемого объекта и делают второй отсчет по шкалам микрометра. Вычисляют разность отсчетов, которая является величиной изображения объекта.
| Рис.4. Объект-микрометр отраженного света с ценой деления шкалы 0.01 мм |
Поскольку цена деления шкалы окуляр-микрометра зависит от увеличения микроскопа, которое может меняться при смене линз, то необходимо производить калибровку шкалы при том увеличении, при котором будут проводиться измерения. Калибровка производится путем сопоставления окулярной шкалы с эталонной, расположенной на объект-микрометре (рис.4).
Для этого на предметный столик микроскопа, вместо препарата помещают объект-микрометр, находит его шкалу и совмещают ее со шкалой окуляр-микрометра (рис.5).
| Рис.5. определение цены деления микрометрической шкалы: 1 – микрометрическая шкала окуляра; 2 – шкала объект-микрометра |
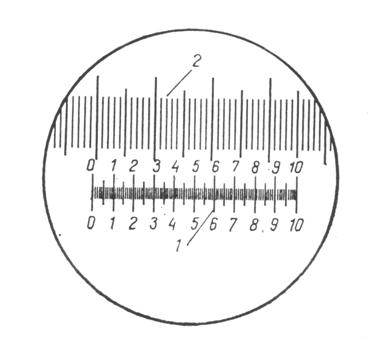
Процедура калибровки, следующая:
1. Определяют сколько делений окуляр-микрометра приходится на какое-то определенное, возможно большее, число делений объект-микрометра.
2. Высчитывают цену деления окуляр-микрометра: L = (N · S )/n, где
L- Цена деления окуляр-микрометра
N- Число делений объект-микрометра
S- Цена одного деления объект-микрометра (см. маркировку)
n- Число делений окуляр-микрометра, совпадающих с числом делений объект-микрометра.
ЛАБОРАТОРНЫЕ РАБОТЫ
Лабораторная работа №1
Исследование преобразователя Холла
Цель работы - изучение принципа действия, применения и основных характеристик датчиков Холла; исследование характеристики преобразования датчика; определение основных параметров датчика.
1.1. Объект испытаний
Датчик холла
1.2. Теоретические сведения
1.2.1. Эффект Холла
Согласно теории электромагнетизма на заряд q, движущийся со скоростью v в магнитном поле, действует сила Лоренца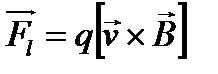 
. где В—индукция магнитного поля. Движущиеся в магнитном поле электрические заряды под воздействием силы Лоренца изменяют свою траекторию.
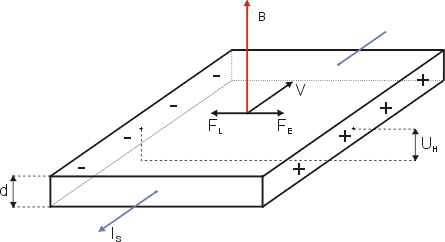
| Рис.1.1. Возникновение разности потенциалов на чувствительном элементе датчика Холла в магнитном поле. |
Если в магнитное поле поместить пластину с током, направление которого перпендикулярно вектору магнитной индукции, то под действием силы Лоренца движущиеся заряды будут отклоняться от направления тока, и на противоположных гранях пластины будут скапливаться заряды разных знаков. Накапливание зарядов будет продолжаться до тех пор, пока возникшее электрическое поле зарядов не скомпенсирует магнитную составляющую силы Лоренца. В результате, на соответствующих сторонах пластины появится разность потенциалов — ЭДС (напряжение Холла), что показано на рис.1.1.