Доказательство. Пусть А и В - выпуклые множества.

Дата: 2025-05-01; Просмотры: 2
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Докажем, что 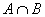- выпуклое множество.

Пусть х, у .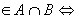

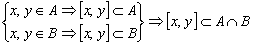Следовательно, 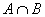- выпуклое множество.

36. Решение систем линейных неравенств

Решение систем линейных неравенств

 

Определение 1. Совокупность точек пространства Rn, координаты которых удовлетворяют уравнению а1х1+ а2х2+…+ anxn = b, называется (n - 1)-мерной гиперплоскостью в n-мерном пространстве.

Теорема 1. Гиперплоскость делит все пространство на два полупространства. Полупространство является выпуклым множеством.

Пересечение конечного числа полупространств является выпуклым множеством.

Теорема 2. Решением линейного неравенства с n неизвестными

а1х1+ а2х2+…+ anxn 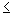b

является одно из полупространств, на которые все пространство делит гиперплоскость

а1х1+ а2х2+…+anxn = b.

Рассмотрим систему из m линейных неравенств с n неизвестными.

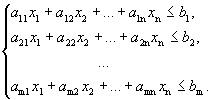
Решением каждого неравенства системы является некоторое полупространство. Решением системы будет являться пересечение всех полупространств. Это множество будет замкнутым и выпуклым.

Решение систем линейных неравенств

с двумя переменными

 

Пусть дана система из m линейных неравенств с двумя переменными.

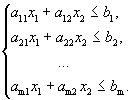
Решением каждого неравенства будет являться одна из полуплоскостей, на которые всю плоскость разбивает соответствующая прямая. Решением системы будет являться пересечение этих полуплоскостей. Данная задача может быть решена графически на плоскости Х10Х2.

37. Представление выпуклого многогранника

Определение 1. Замкнутое выпуклое ограниченное множество в Rn, имеющее конечное число угловых точек, называется выпуклым n-мерным многогранником.

Определение 2. Замкнутое выпуклое неограниченное множество в Rn , имеющее конечное число угловых точек, называется выпуклой многогранной областью.

Определение 3. Множество А 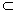Rn называется ограниченным, если найдется n-мерный шар, содержащий это множество.

Определение 4. Выпуклой линейной комбинацией точек 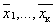называется выражение 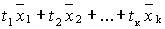, где ti , .

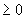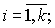
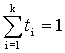Теорема (теорема о представлении выпуклого многогранника). Любую точку выпуклого многогранника можно представить в виде выпуклой линейной комбинации его угловых точек.

38. Область допустимых решений системы уравнений и неравенств.

 

Пусть дана система из m линейных уравнений и неравенств с n неизвестными.

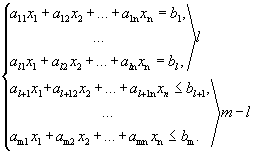
Определение 1. Точка 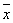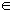Rn называется возможным решением системы, если ее координаты удовлетворяют уравнениям и неравенствам системы. Совокупность всех возможных решений называется областью возможных решений (ОВР) системы.

Определение 2. Возможное решение, координаты которого неотрицательны, называется допустимым решением системы. Множество всех допустимых решений называется областью допустимых решений (ОДР) системы.

Теорема 1. ОДР является замкнутым, выпуклым, ограниченным (или неограниченным) подмножеством вRn.

Теорема 2. Допустимое решение системы является опорным тогда и только тогда, когда эта точка являетсяугловой точкой ОДР.

Теорема 3 (теорема о представлении ОДР). Если ОДР - ограниченное множество, то любое допустимое решение можно представить в виде выпуклой линейной комбинации угловых точек ОДР (в виде выпуклой линейной комбинации опорных решений системы).

Теорема 4 (теорема о существовании опорного решения системы). Если система имеет хотя бы одно допустимое решение (ОДР 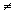Æ), то среди допустимых решений существует хотя бы одно опорное решение.