2. Из вида уравнения следует, что линия симметрична относительно оси OX.

Дата: 2025-05-01; Просмотры: 2

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

3. 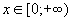. Следовательно, кривая расположена правее оси OY.

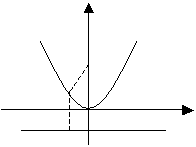
Построим данную кривую.

Y

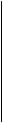N (- p /2, y ) M ( x , y )

X

K(-p/2,0) 0 F(p/2,0)

x =- p /2

Если парабола симметрична относительно OY и имеет вершину в начале координат, то ее каноническое уравнение имеет вид .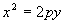

Y

F

0 X

32. Преобразование прямоугольной системы координат.

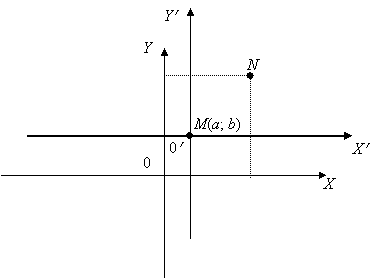
Предположим, что система координат XOY перенесена параллельно себе так, что начало координат сместилось в точку M(a;b). Найдем связь между координатами любой точки в старой и новой системе координат. Возьмем произвольную точку N. В плоскости XOY она имеет координаты N(x; y), в плоскости 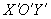она имеет координаты .

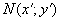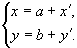
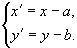
- преобразование координат при параллельном переносе; выражение старых координат через новые и новых через старые.

Поворот системы координат

Y

Y ¢

M X ¢

b a

N X

0 K

Предположим, что прямоугольную систему координат повернули на угол a в положительном направлении и получили новую систему координат .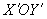

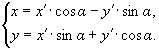
Эти соотношения описывают преобразование координат при повороте, они выражают старые координаты через новые. Из этих соотношений можно выразить новые координаты. Выражение новых координат через старые:

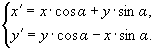
33. Уравнение плоскости в пространстве. Условия параллельности и перпендикулярности плоскостей.

Теорема . Всякое невырожденное уравнение первой степени с тремя переменными описывает некоторую плоскость в пространстве, и наоборот: всякая плоскость может быть описана таким уравнением.

Ax + By + Cz + D = 0 - общее уравнение плоскости,

A² + B² + C² ¹ 0 - условие невырожденности.

Рассмотрим различные случаи расположения плоскости в пространстве в зависимости от коэффициентов общего уравнения.

1. D = 0, Ax + By + Cz = 0 - проходит через начало координат;

A = 0, By + Cz + D = 0 - параллельна оси ОХ;

B = 0, Ax + Cz + D = 0 - параллельна оси OY;

C = 0, Ax + By + D = 0 - параллельна оси OZ;

2. A = D = 0, By + Cz = 0 - содержит OX;

B = D = 0, Ax + Cz = 0 - содержит OY;

C = D = 0, Ax + By = 0 - содержит OZ;

A = B = 0, Cz + D = 0 - параллельна плоскости XOY;

A = C = 0, By + D = 0 - параллельна плоскости XOZ;

B = C = 0, Ax + D = 0 - параллельна плоскости YOZ;

3. A = B = D = 0, Cz = 0 - совпадает с плоскостью XOY;

A = C = D = 0, By = 0 - совпадает с плоскостью XOZ;

B = C = D = 0, Ax = 0 - совпадает с плоскостью YOZ.

Расстояние от точки M₀ (x₀, y₀, z₀) до плоскости, заданной общим уравнением Ax + By + Cz + D = 0, вычисляется по формуле

.

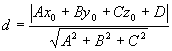Условия параллельности

и перпендикулярности плоскостей

Даны две плоскости, заданные общими уравнениями:

A₁x + B₁y + C₁z + D₁ = 0,

A₂x + B₂y + C₂z + D₂ = 0.

Они имеют нормальные векторы:

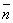₁(A₁, B₁, C₁),

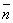₂(A₂, B₂, C₂).

1. Если плоскости параллельны, то векторы нормалей коллинеарны.

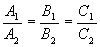- условие параллельности плоскостей.

2. Если плоскости перпендикулярны, то векторы нормалей ортогональны.

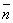_{1 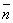2} = 0,

A₁A₂ + B₁B₂ + C₁C₂ = 0 - условие перпендикулярности плоскостей.

34. Уравнение прямой в пространстве

Каноническое уравнение прямой в пространстве

Пусть прямая проходит через точку M₁ (x₁, y₁, z₁) и параллельна вектору 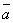(m , n , l). Составим уравнение этой прямой.

Z

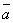
M

M₁

Y

X

Возьмем произвольную точку M (x , y , z) на этой прямой и найдем зависимость между x , y , z. Построим вектор

.

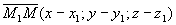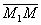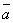Векторы и коллинеарны.

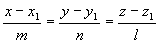- каноническое уравнение прямой в пространстве.

Уравнение прямой в пространстве,

проходящей через две данные точки

Пусть прямая проходит через две точки M₁ (x₁, y₁, z₁) и M₂(x₂, y₂, z₂). Составим ее уравнение. Рассмотрим вектор 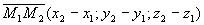. Данная прямая параллельна этому вектору и проходит через точку M₁ (x₁, y₁, z₁). Используя каноническое уравнение, получаем

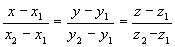
- уравнение прямой, проходящей через две данные точки.

35. Метрическое пространство, выпуклые множества.

Евклидово пространство. Выпуклые множества

Определение 1. Упорядоченная совокупность из n действительных чисел 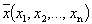называется n-мерной точкой.

Определение 2. Расстоянием между двумя n-мерными точками 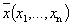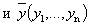называется величина

.

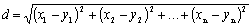Определение 3. Совокупность всех n-мерных точек с введенной на ней метрикой 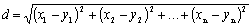называется n-мерным евклидовым (метрическим) пространством Rⁿ.

Определение 4. 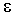-окрестностью точки 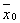в Rⁿ называется множество точек 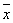, удовлетворяющих условию .

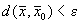Определение 5. Множество А 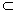Rⁿ называется открытым, если любая точка входит в него вместе с некоторой окрестностью.

Определение 6. Множество B 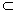Rⁿ называется замкнутым, если оно является дополнением до некоторого открытого множества.

В - замкнутое ó Rⁿ \ B - открытое.

Определение 7. Отрезком в Rⁿ , соединяющим точк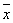и и 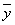, называется множество точек, удовлетворяющее условию .

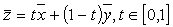Определение 8. Множество А 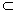Rⁿ называется выпуклым, если вместе с любыми двумя точками, входящими в него, оно содержит отрезок, их соединяющий.

Выпуклые множества. Невыпуклые множества.

Определение 9. Точка х 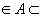Rⁿ называется угловой точкой множества А, если она не является внутренней ни для какого отрезка, целиком лежащего в А.

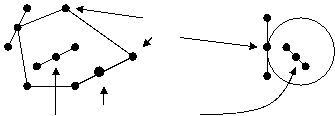Угловые точки

Неугловые точки

Теорема. Пересечение конечного числа выпуклых множеств есть выпуклое множество.