Справедливы следующие свойства решений однородной и неоднородной систем.

Дата: 2025-05-01; Просмотры: 3
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Теорема 1 . Линейная комбинация решений однородной системы (1) является решением системы (1).

 

Доказательство. Пусть и - решения однородной системы.

 

Рассмотрим , где - некоторые произвольные числа. Так как , и являются решениями, то , и . Найдем .

является решением системы (1).

Теорема 2 . Разность двух решений неоднородной системы (2) является решением однородной системы (1).

Доказательство. Пусть и - решения системы (2). Рассмотрим

.. является решением однородной системы (1).

Теорема 3 . Сумма решения однородной системы (1) с решением неоднородной системы (8.2) есть решение неоднородной системы (2).

Пусть - решение системы (1), - решение системы (2). Покажем, что - решение системы (2).

Доказательство. ,

. является решением неоднородной системы (2).

 

24. Прямая линия на плоскости. Общее уравнение, уравнение с угловым

Коэффициентом

 

Общее уравнение прямой

 

Теорема 1 . Всякое невырожденное уравнение первой степени с двумя переменными определяет на плоскости некоторую прямую, и наоборот.

А x+В y+С=0 - общее уравнение прямой,

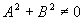- условие невырожденности.

Рассмотрим различные случаи расположения прямой на плоскости в зависимости от коэффициентов общего уравнения.

1) С = 0, Ax + By = 0 - прямая проходит через начало координат;

А = 0, By + C = 0 - прямая проходит параллельно оси ОХ;

В = 0, Ax + C = 0 - прямая проходит параллельно оси ОУ;

2) A = C = 0, By = 0 - прямая совпадает с осью ОХ;

B = C = 0, Ax = 0 - прямая совпадает с осью ОУ.

Расстояние от точки M0 (x0,y0) до прямой, заданной общим уравнением Ax + By + C = 0, находится по формуле

.

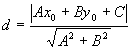равнение прямой с угловым коэффициентом

 

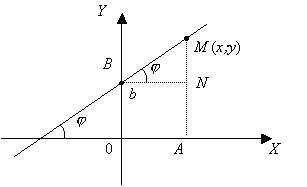
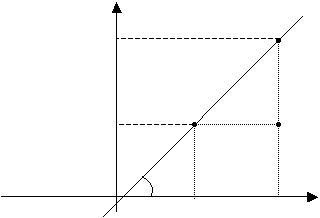
Предположим, что прямая расположена под углом j к оси ОХ и отсекает от оси ОУ отрезок в b единиц. Составим уравнение этой прямой.

 
 

 

 


Возьмем произвольную точку M (x , y), лежащую на этой прямой, и найдем уравнение, связывающее переменные x и y. Из рисунка видно: AM = AN + NM, где AM = y, AN = b. Из треугольника BMN : MN = BN · tg j .Обозначим tg j = k и назовем его угловым коэффициентом прямой. MN = k · x.

Подставляя в равенство

AM = AN + NM

выражения отрезков

AM = y, AN = b, MN = k · x;

получим

y = k · x + b - уравнение прямой с угловым коэффициентом.

25. Уравнение прямой, проходящей через данную точку в данном направлении.

Предположим, что прямая проходит через точку M1 (x1,y1) и образует с осью OX угол j. Составим уравнение этой прямой.

 

 

Y

y M ( x , y )

у1 M1 (x1,y1) N

j

0 х1 х Х

 

Будем искать уравнение прямой в виде уравнения с угловым коэффициентом: y = k · x + b. Угловой коэффициент прямой можно найти, зная угол наклона k = tg j. Возьмем произвольную точку M (x , y), лежащую на этой прямой, и найдем уравнение, связывающее переменные x и y. Так как точки М и M1 лежат на прямой, то их координаты удовлетворяют уравнению прямой:

y = k · x + b ,

y1 = k · x1 + b .

Вычитая эти равенства, получим:

y - y1 = k · (x - x1) - уравнение прямой, проходящей через данную точку в данном направлении.

26. Уравнения прямой, проходящей через две данные точки и в отрезках на осях.

Даны две точки M1 (x1, y1) и M2 (x2, y2). Составим уравнение прямой, проходящей через две эти точки.

Из треугольника M1M2M:

,

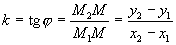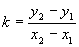
- угловой коэффициент прямой, проходящей через две данные точки.

 

Y

y2 M2 (x2, y2)

у1 M1 (x1,y1) M

j

0 х1 х2 Х

Воспользуемся уравнением прямой, проходящей через данную точку M1 и в данном направлении :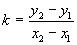

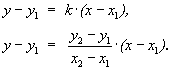
Если точки имеют различные абсциссы и ординаты, то, умножая обе части последнего равенства на величину

,

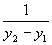получим

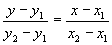- уравнение прямой, проходящей через две данные точки.

Если точки имеют одинаковые абсциссы или одинаковые ординаты, то используют формулу .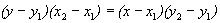

27. Угол между двумя прямыми. Условия параллельности и перпендикулярности прямых.

Определение 1. Углом между двумя прямыми I и II называется угол, отсчитываемый в положительном направлении от прямой I к прямой 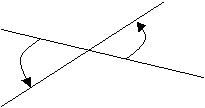II.

II

I

 

Пусть даны две прямые, заданные уравнениями с угловыми коэффициентами

y = k1 · x + b1, y = k2 · x + b2.

Найдем угол между первой и второй прямыми. Обозначим углы наклона прямых j1 и j2. Тогда

k1 = tgj1 , k2 = tgj2.

Проведем через точку пересечения прямую, параллельную оси OX.

 
 

 

 


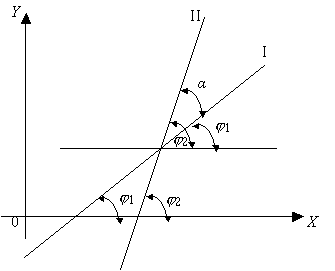
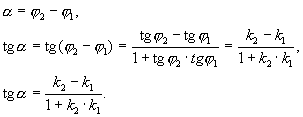
- формула для вычисления угла между двумя прямыми.

1. Предположим, что прямые параллельны:

a = 0 Þ tg a = 0 Þ

k1 = k2 - условие параллельности прямых.

2. Предположим, что прямые перпендикулярны:

a = 900 Þ tg a не существует Þ ctg a = 0 Þ

Þ k1 · k2 = -1 - условие перпендикулярности прямых.

28. Эллипс.

Определение 1. Геометрическое место точек, сумма расстояний от каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная, называется эллипсом.

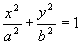- каноническое уравнение эллипса.

Исследуем форму эллипса.

1. Найдем точки пересечения с осями.

OX: y = 0, ;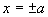

OY: x = 0, ;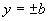

A(a; 0); B (-a; 0); C (0; b); D (0; -b).

Определение 2. Точки A, B, C, D называются вершинами эллипса.

2. Из вида уравнения следует, что линия симметрична относительно осей OX и OY и начала координат.

3.

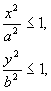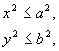Þ Þ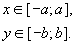

Следовательно, кривая расположена в прямоугольнике со сторонами 2а и 2b.

Построим данную кривую.

 

Y

 

b

- a F1 F2 a

X

 

-

-b

 

Определение 3. Отношение фокусного расстояния к большой оси эллипса называется эксцентриситетом эллипса.

.

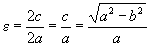Определение 4. Параметр a называется большой полуосью эллипса, параметр b называется малой полуосью эллипса.

29. Окружность.

Определение . Геометрическое место точек, расстояние от каждой из которых до данной точки О, называемой центром, есть величина постоянная, называется окружностью.

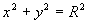- каноническое уравнение окружности.

Окружность является частным случаем эллипса, когда большая и малая полуоси равны, с = 0, фокусы сливаются в центр. Эксцентриситет окружности равен нулю.

.

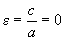30. Гипербола.

Определение 1. Геометрическое место точек, разность расстояний от каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная, называется гиперболой.

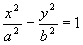- каноническое уравнение гиперболы.

Исследуем форму гиперболы.

1. Найдем точки пересечения с осями.

OX: y = 0, 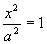, , 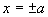A(a;0) , B(-a;0).

OY: x = 0, , .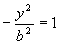

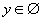Определение 2. Точки A и B называются вершинами гиперболы.

2. Из вида уравнения следует, что линия симметрична относительно осей OX, OY и начала координат.

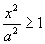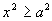3. Þ Þ .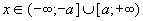

Следовательно, кривая расположена вне прямоугольника со сторонами 2а и 2b.

Построим данную кривую.

 
 

 

 


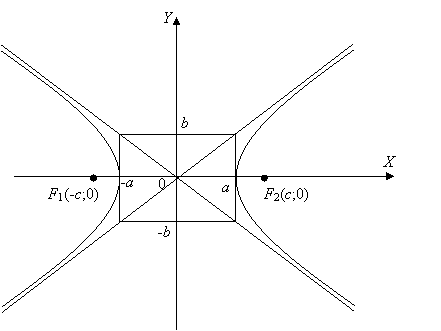
Определение 3. Параметр a называется действительной полуосью гиперболы, а параметр b называется мнимой полуосью.

Определение 4. Прямые 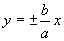называются асимптотами гиперболы.

При возрастании х гипербола неограниченно приближается к асимптотам.

Определение 5. Отношение фокусного расстояния гиперболы к ее действительной оси называется эксцентриситетом.

.

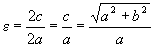Определение 6. Кривые эллипс, гипербола, окружность называются кривыми второго порядка с эксцентриситетом, причем для окружности 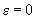, для эллипса 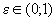и для гиперболы 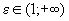. При 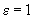гипербола вырождается в две параллельные прямые.

 

31. Парабола.

Определение 1. Геометрическое место точек, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой, именуется параболой.

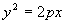
- каноническое уравнение параболы с вершиной в начале координат, симметричной относительно оси OX.

Исследуем форму параболы.

1. Найдем точки пересечения с осями.

OX , OY : y = 0, х=0, О(0;0).

Определение 2. Точка A называется вершиной параболы.