, где - главный определитель, - j-й вспомогательный определитель, который получен из определителя заменой j-го столбца столбцом свободных членов.
Если главный определитель равен нулю и хотя бы один их вспомогательных определителей отличен от нуля, то система решений не имеет.
Если главный определитель и все вспомогательные определители равны нулю, то система имеет бесконечно много решений.
18. Нахождение решений общей системы уравнений.
Пусть дана неоднородная система m линейных уравнений с n неизвестными
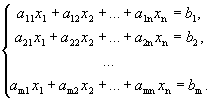
Предположим, что система совместна, т.е. r ( A )=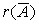 
= r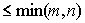 
. Следовательно, существует минор порядка rматрицы А, отличный от нуля. Предположим, что он расположен в левом верхнем углу матрицы. Если это не так, то можно переставить уравнения и перенумеровать неизвестные.
.
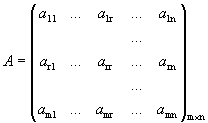Первые r уравнений системы линейно независимы. Остальные выражаются через них. Следовательно, их можно отбросить.
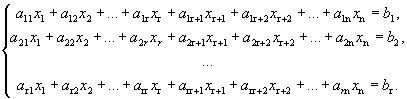
Определение 1. Переменные, коэффициенты при которых образуют минор, отличный от нуля (базисный минор), называются базисными переменными (x1, x2, …, xr). Остальные переменные xr+1, …, xn называются свободными.
Дадим свободным переменным произвольные числовые значения xr+1=сr+1, xr+2=сr+2, …, xn= cn.
Запишем систему в виде
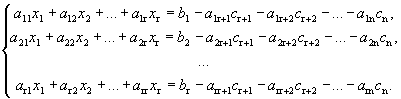
Мы получили систему из r линейных уравнений с r неизвестными, определитель которой отличен от нуля. Она имеет единственное решение.
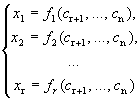- общее решение.
Определение 2. Выражение базисных переменных через свободные называется общим решением системы.
Определение 3. Решение системы, полученное из общего при конкретных значениях свободных переменных, называется частным решением. Частных решений у системы бесконечно много, все они содержатся в общем решении.
Определение 4. Частное решение, полученное из общего, когда свободные переменные равны нулю, называется базисным решением системы.
Определение 5. Базисное решение, координаты которого неотрицательны, называется опорным решением системы.
19. Метод Гаусса. Нахождение опорных решений
Определение 1. Элементарными преобразованиями системы называются:
1) умножение уравнения на число, отличное от нуля;
2) прибавление к одному уравнению другого уравнения, умноженного на некоторое число, отличное от нуля.
3) перестановка двух уравнений;
4) отбрасывание уравнения 0=0.
Если получено уравнение 0=k, то система несовместна.
Метод Гаусса состоит в приведении системы к диагональному виду путем последовательного исключения неизвестных. Количество исключенных неизвестных равно числу линейно независимых уравнений. Переменная считается исключенной, если она содержится только в одном уравнении с коэффициентом 1.
Метод Гаусса удобно применять к расширенной матрице системы, левую часть которой с помощью элементарных преобразований матрицы нужно привести к единичной матрице.
20. Совместность однородной системы.
Рассмотрим однородную систему
.
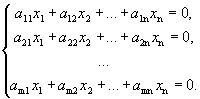Однородная система всегда совместна, так как всегда имеет тривиальное (нулевое) решение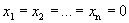 
. Выясним, когда данная система имеет нетривиальное решение.
Теорема 1 . Однородная система имеет нетривиальное решение тогда и только тогда, когда ранг матрицы, составленной из коэффициентов при неизвестных, меньше числа неизвестных.
Доказательство. Пусть система совместна. Это может быть тогда и только тогда, когда найдутся числа с1, с2, …, сn, при подстановке которых в систему мы получим m тождеств. Эти m тождеств можно записать в виде
.
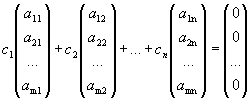Следовательно, система векторов-столбцов матрицы А линейно зависима. А это может быть тогда и только тогда, когда ранг системы векторов-столбцов меньше n, т.е. r ( A )< n.
Следствие. Квадратная однородная система имеет нетривиальное решение тогда и только тогда, когда определитель матрицы, составленной из коэффициентов при неизвестных, равен нулю.
Доказательство. Так как r ( A )< n, то столбцы матрицы линейно зависимы и, следовательно, определитель матрицы равен нулю.
21. Системы однородных уравнений. Свойства решений, совместность.
Рассмотрим однородную систему
.
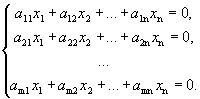Однородная система всегда совместна, так как всегда имеет тривиальное (нулевое) решение 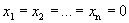. Выясним, когда данная система имеет нетривиальное решение.
Теорема 1 . Однородная система имеет нетривиальное решение тогда и только тогда, когда ранг матрицы, составленной из коэффициентов при неизвестных, меньше числа неизвестных.
Доказательство. Пусть система совместна. Это может быть тогда и только тогда, когда найдутся числа с1, с2, …, сn, при подстановке которых в систему мы получим m тождеств. Эти m тождеств можно записать в виде
.
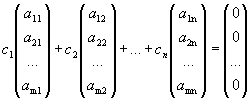Следовательно, система векторов-столбцов матрицы А линейно зависима. А это может быть тогда и только тогда, когда ранг системы векторов-столбцов меньше n, т.е. r ( A )< n.
Следствие. Квадратная однородная система имеет нетривиальное решение тогда и только тогда, когда определитель матрицы, составленной из коэффициентов при неизвестных, равен нулю.
Доказательство. Так как r ( A )< n, то столбцы матрицы линейно зависимы и, следовательно, определитель матрицы равен нулю.
22. Системы однородных уравнений. Общее рещение систем.
Система
(1)
всегда имеет тривиальное решение. Если ранг матрицы, составленной из коэффициентов при неизвестных, меньше числа неизвестных, то система (1) имеет нетривиальные решения.
1) r ( A )= n - система (1) имеет только тривиальное решение:
2) r ( A )= r < n - система (1) имеет нетривиальные решения.
Количество свободных переменных во втором случае будет равно n - r, а базисных r. Давая свободным переменным произвольные значения, мы будем получать различные решения системы (1), т.е. любому вектору размерности n - r(сr+1, cr+2, …, cn)будет соответствовать решение системы (1)(с1, c2, …, cr, cr+1, …, cn).
Определение. Фундаментальной системой решений однородной системы (1) называется максимальная линейно независимая система решений системы (1). Фундаментальная система содержит n - r линейно независимых решений системы (1).
Чтобы получить фундаментальную систему решений, нужно в (n - r)-мерном пространстве взять линейно независимую систему из n - r векторов и по ним построить соответствующие решения системы (1). Полученные решения будут образовывать фундаментальную систему решений . Так как эта система максимальна, то любое решение системы (1) можно представить в виде линейной комбинации решений фундаментальной системы
. Полученное выражение является общим решением однородной системы (1)
23. Однородные системы линейных уравнений
дана однородная система
Рассмотрим соответствующую неоднородную систему
С помощью матриц эти системы можно записать в матричном виде.