Для данной матрицы можно составить m · n миноров первого порядка, миноров второго порядка и т.д., миноров k-го порядка.

Дата: 2025-05-01; Просмотры: 2

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Определение 1. Рангом матрицы называется максимальный порядок минора, отличного от нуля, и обозначаетсяr ( A ).

Очевидно, что .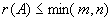

Определение 2. Отличный от нуля минор порядка r= r ( A ) называется базисным минором матрицы А, а строки (столбцы), в которых он расположен, называют базисными строками (столбцами).

Теорема 1 (теорема о базисном миноре). Любой столбец (строка) матрицы А является линейной комбинацией ее базисных столбцов (строк).

Теорема 2 . Ранг матрицы равен максимальному числу линейно независимых строк (столбцов) матрицы.

При элементарных преобразованиях ранг матрицы не меняется. Ранг треугольной матрицы равен числу ненулевых строк этой матрицы.

Для того чтобы найти ранг матрицы, необходимо с помощью элементарных преобразований привести ее к треугольному виду и найти ранг полученной матрицы. Рассмотрим схему таких преобразований подробно. Пусть дана матрица

А= .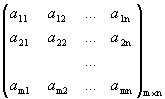

Предположим, что а₁₁ отличен от нуля (если а₁₁=0, то, переставив строки, этого можно добиться). Разделим первую строку на а₁₁, после чего на первом месте в первой строке будет стоять 1. Умножая последовательно первую строку на а₂₁, а_31, …, а_m1 и вычитая, соответственно, из второй, третьей, …, n-й, образуем в первом столбце все нулевые элементы.

А~ .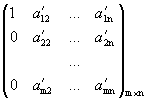

Преобразуем второй столбец, начиная с элемента а’₂₂. Если этот элемент отличен от нуля, то аналогично вышеизложенному получим на его месте единицу, а ниже расположенные элементы превратим в нули. Если а’₂₂=0, но ниже его в том же столбце есть элемент, отличный от нуля, то, поменяв местами строки, переставим его на место а’₂₂. Если в столбце не окажется ненулевых элементов, то можно поменять местами столбцы, пока на месте а’₂₂ не окажется ненулевой элемент.

После второго цикла получим новую эквивалентную матрицу.

А~ .

Выполняя последовательно несколько циклов подобных эквивалентных преобразований и отбросив нулевые строки, придем окончательно к матрице

А~ .

Буквой "а" условно обозначены элементы матрицы, которые могут принимать любые числовые значения.

Очевидно, что r ( A )= m1, так как минор, расположенный в первых m1 строках и первых m1 столбцах, равен единице.

Вычисление ранга системы векторов можно свести к вычислению ранга матрицы. Из теоремы 2 следует, что ранг системы векторов равен рангу матрицы, столбцами (строками) которой являются векторы этой системы.

14. Собственные векторы и собственные значения матрицы.

Определение. Число 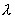называется собственным значением квадратной матрицы А, если найдется вектор 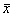такой, что А· 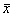= 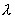· 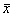. Вектор 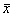называется собственным вектором матрицы А, соответствующим данному собственному значению.

Теорема 1 . Собственные значения матрицы А являются решениями уравнения

.

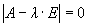Это уравнение называется характеристическим уравнением матрицы А.

Теорема 2 . Число различных собственных значений квадратной матрицы не превосходит ее порядка. Собственные векторы, отвечающие различным собственным значениям, линейно независимы.

15. Системы линейных уравнений.

Определение 1. Система вида

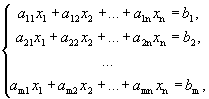
называется системой m линейных уравнений с n неизвестными, где x₁, x₂, …, x_n - неизвестные, a_ij, i = 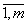, j = 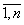- коэффициенты при неизвестных, b₁, b₂, …, b_m - свободные члены.

Определение 2. Если все свободные члены равны нулю, то система называется однородной, и неоднородной - в противном случае.

Определение 3. Решением системы называется совокупность из n чисел с₁, с₂, …, с_n, при подстановке которой в систему вместо неизвестных будет получено m числовых тождеств.

Определение 4. Система называется совместной, если она имеет хотя бы одно решение, и несовместной в противном случае.

Определение 5. Совместная система называется определенной, если она имеет единственное решение, и неопределенной - в противном случае.

При изучении систем исследуют три вопроса:

1) совместна система или нет;

2) если система совместна, то является ли она определенной или неопределенной;

3) нахождение единственного решения в случае определенной системы и всех решений в случае неопределенной.

16. Совместность неоднородной системы.

Рассмотрим неоднородную систему:

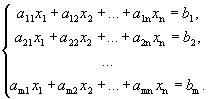
Рассмотрим матрицы:

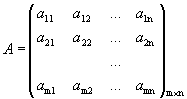и .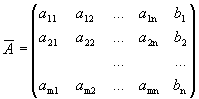

Матрица 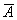называется расширенной матрицей системы.

Теорема (теорема Кронекера - Капелли) . Неоднородная система линейных уравнений совместна тогда и только тогда, когда ранг матрицы, составленной из коэффициентов при неизвестных, равен рангу расширенной матрицы.

Доказательство. Необходимость. Пусть система совместна, тогда найдутся числа с₁, с₂, …, с_n, при подстановке которых в систему мы получим m тождеств, которые можно записать в виде одного векторного тождества:

.

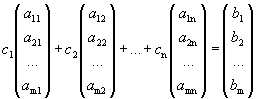Следовательно, вектор-столбец свободных членов является линейной комбинацией векторов-столбцов матрицы А, тогда добавление его к системе векторов-столбцов матрицы А не меняет ранга системы. Отсюда r ( A )= .

Достаточность. Пусть r ( A )= = r. Следовательно, существует линейно независимая подсистема из r векторов-столбцов матрицы A. Она же будет содержатся и в матрице 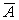. Так как эта система максимальна, то вектор-столбец свободных членов будет выражаться через эти r векторов-столбцов. Следовательно, вектор-столбец свободных членов можно представить в виде линейной комбинации всех векторов-столбцов матрицы А, т.е. найдутся числа с₁, с₂, …, с_nтакие, что вектор-столбец будет представлен в виде

.

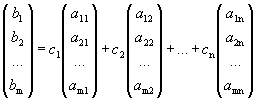Следовательно, числа с₁, с₂, …, с_n являются решением системы, т.е. она совместна.

17. Решение систем методом Крамера и с помощью обратной матрицы.

Рассмотрим неоднородную систему n линейных уравнений с n неизвестными:

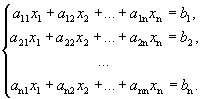
Теорема (теорема Крамера) . Если определитель матрицы, составленной из коэффициентов при неизвестных, отличен от нуля ( 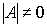), то система имеет единственное решение, которое можно найти по формулам Крамера: