Доказательство. Пусть система имеет базис .

Дата: 2025-05-01; Просмотры: 3
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

1)Линейное векторное н-мерное пространство

Определение 1. Упорядоченная совокупность из n действительных чисел (а1, а2, …, аn) называется n-мерным вектором ā(а1, а2, …, аn). Числа а1, а2, ..., аn называются координатами вектора.

Два n-мерных вектора (а1, а2, …, аn) и (b1, b2, …, bn) считаются равными, если равны их соответствующие координаты:

, ( ).

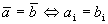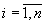Вектор, все координаты которого равны нулю, называется ноль-вектором и обозначается .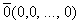

Определение 2. Суммой (разностью) двух n-мерных векторов (а1, а2, …, аn) и (b1, b2, …, bn) называется n-мерный вектор, координаты которого равны суммам (разностям) соответствующих координат исходных векторов:

=(a1 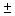b1; a2 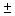b2; …; a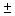n bn).

Определение 3. Произведением n-мерного вектора (а1, а2, …, аn) на число k называется n‑мерный вектор, координаты которого равны произведениям координат вектора на число k:

k · =(ka1; ka2; …; kan).

Для геометрических векторов (n<4) эти операции эквивалентны правилу параллелограмма или треугольника и растяжению (сжатию) вектора.

Свойства операций над векторами:

1) 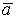+ 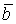= + - коммутативность,

2) +( + 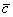)=( + )+ 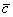- ассоциативность,

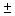
3) k·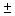( )=k · k · - дистрибутивность,

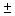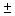4) (k1 k2)· = k1 · k2· ,

5) (k1·k2)· =k1·(k2· ),

6) 1· = ,

7) 0· = ,

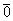8) k· = ,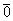

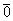9) k· = .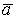

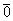
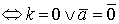Определение 4. Совокупность всех n-мерных векторов с введенными на ней операциями сложения и умножения на число называется n-мерным линейным векторным пространством и обозначается En.

2) Скалярное произведение. Угол между векторами.

Определение 1. Скалярным произведением двух n-мерных векторов (а1, а2, ..., аn) и (b1, b2, ..., bn) называется число, равное сумме попарных произведений соответствующих координат.

· =а1·b1+a2·b2+…+an·bn.

Свойства скалярного произведения:

1. · = · - коммутативность;

2. ·( + 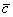)= · + · 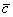- дистрибутивность;

3. k·( · )=(k· )· ,

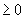4. · = 2 , 2=0 .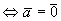

Определение 2. Длиной n-мерного вектора называется величина:

.

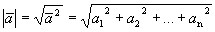Определение 3. Углом между двумя ненулевыми n-мерными векторами называется угол, косинус которого вычисляется по формуле

.

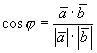3) Условие коллинеарности и ортогональности векторов.

Определение 1. Два n-мерных вектора и называются коллинеарными, если найдется число 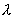такое, что = · .

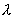Рассмотрим два коллинеарных вектора и . Так как они коллинеарны, то = 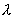· , или (a1, a2, …, an)=(l b1, l b2, …, l bn ). Следовательно, a1= l b1, a2=l 2, …, an=l bn.

Выражая из этих равенств l, получим

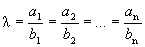- условие коллинеарности.

Для того чтобы два вектора были коллинеарными, необходимо и достаточно, чтобы их координаты были пропорциональны.

Найдем угол между коллинеарными векторами.

.

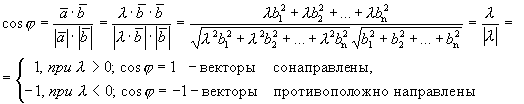Определение 2. Два ненулевых n-мерных вектора и называются ортогональными, или перпендикулярными, если угол между ними равен 90°.

,

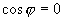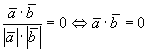- условие ортогональности.

4) Системы векторов.

Пусть дана система n-мерных векторов .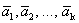

Определение 1. Линейной комбинацией системы векторов называется выражение вида

,

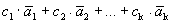где с1, с2, …, сk - некоторые числа.

Определение 2. Выпуклой линейной комбинацией системы векторов называют линейную комбинацию, в которой все коэффициенты неотрицательны и сумма всех коэффициентов равна единице.

; , ; .

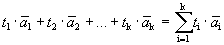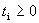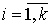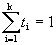Определение 3. Вектор 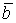разлагается по системе векторов 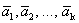, если его можно представить в виде линейной комбинации векторов этой системы.

.

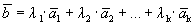5) Ранг и базис системы векторов и всего пространства.

Определение 1. Рангом системы векторов называется максимальное число линейно независимых векторов системы.

.

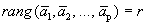Определение 2. Базисом системы векторов называется максимальная линейно независимая подсистема данной системы векторов.

Теорема. Любой вектор системы можно представить в виде линейной комбинации векторов базиса системы. (Всякий вектор системы можно разложить по векторам базиса.) Коэффициенты разложения определяются для данного вектора и данного базиса однозначно.

Доказательство. Пусть система 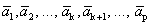имеет базис .

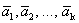1 случай. Вектор 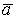- из базиса. Следовательно, он равен одному из векторов базиса, допустим 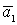. Тогда = .

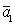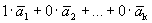2 случай. Вектор 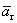- не из базиса. Тогда r>k.

Рассмотрим систему векторов 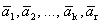. Данная система является линейно зависимой, так как 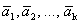- базис, т.е. максимальная линейно независимая подсистема. Следовательно, найдутся числа с1, с2, …, сk, с, не все равные нулю, такие, что

= .

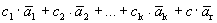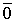Очевидно, что 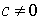(если с=0, то базис системы является линейно зависимым).

.

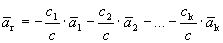Докажем, что разложение вектора по базису единственно. Предположим противное: имеется два разложения вектора по базису.

= ,

= .

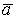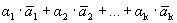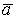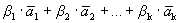Вычитая эти равенства, получим

.

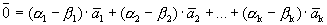Учитывая линейную независимость векторов базиса, получим

.

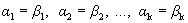Следовательно, разложение вектора по базису единственно.

Количество векторов в любом базисе системы одинаково и равно рангу системы векторов.

Ранг и базис n‑мерного линейного

векторного пространства

 

Теорема 1. Ранг n-мерного пространства равен его размерности: r=n.

Доказательство. На основании теоремы Штейница ранг не превышает n. С другой стороны, в пространстве имеется система из n линейно независимых единичных векторов, следовательно, ранг не меньше n. Значит, базис содержит nвекторов.

Следствие 1. Любой базис n-мерного пространства состоит из n линейно независимых n-мерных векторов.

Следствие 2. Любая система в n-мерном пространстве, содержащая больше чем n векторов, линейно зависима.

Следствие 3. Любой вектор пространства можно однозначно разложить по векторам любого базиса. Коэффициенты разложения для данного вектора и данного базиса определяются единственным образом. Коэффициенты разложения называются координатами данного вектора в этом базисе.

6) Ортогональные системы векторов

Определение. Система ненулевых векторов 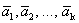называется ортогональной, если все векторы этой системы попарно ортогональны.

Теорема. Ортогональная система ненулевых векторов линейно независима.

7) Матрицы. Операции над матрицами.

Определение 1. Прямоугольная таблица чисел вида

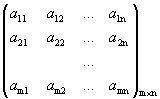
называется прямоугольной матрицей размера 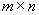, где m - количество строк, а n - количество столбцов.

Определение 2. Числа, которые образуют матрицу, - aij, где 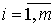, , 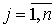называются элементами матрицы.

Определение 3. Числа i и j называются индексами элемента aij, i показывает, в какой строке расположен данный элемент, а j - в каком столбце находится этот элемент.

Две матрицы считаются равными, если равны их соответствующие элементы.

Операции над матрицами

 

Определение 1. Транспонированием матрицы называется такое преобразование матрицы, при котором строки и столбцы меняются ролями при сохранении номеров. Транспонированная матрица обозначается АТ.

, , .

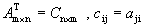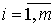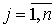Для квадратной матрицы это преобразование эквивалентно симметричному отображению относительно главной диагонали.

Определение 2. Суммой (разностью) двух матриц одинакового порядка называется матрица того же порядка, каждый элемент которой равен сумме (разности) соответствующих элементов исходных матриц.

, , .

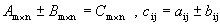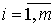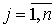Определение 3. Произведением матрицы на число называется матрица того же размера, каждый элемент которой равен произведению соответствующего элемента исходной матрицы на это число.

, , .

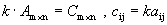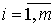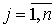Определение 4. Произведением двух матриц А и В, размеры которых заданы соотношением: количество столбцов первой матрицы равно количеству строк второй, называется матрица С, у которой количество строк равно количеству строк первой матрицы, а количество столбцов равно количеству столбцов второй. Каждый элемент данной матрицы равен сумме попарных произведений элементов соответствующей строки первой матрицы и элементов соответствующего столбца второй.

, , , .

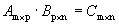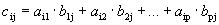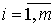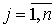Приведем свойства операций над матрицами.

1. А · В 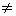В · А - произведение матриц не коммутативно.

2. А+В = В+А - сложение матриц коммутативно.

3. (А + В) +С = А + (В + С) - ассоциативность.

4. ,

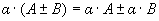5. ,

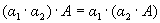6. ,

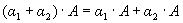7. 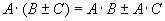- дистрибутивность.

8. 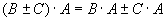- дистрибутивность.

9. А · Е=Е · А=А.

10. .

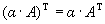11. .

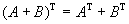12. .

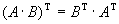8) Определители. Их свойства.

Определители

 

Пусть дана квадратная матрица порядка n:

А = .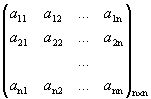

Определение 1. Определителем n-го порядка матрицы А называется число, равное алгебраической сумме n!слагаемых, каждое из которых равно произведению n элементов матрицы А 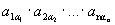, взятых по одному из каждой строки и каждого столбца, причем каждое слагаемое берется со знаком "+" или "-".

.

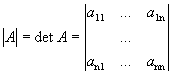Мнемоническое правило вычисления определителя второго порядка:

 

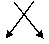
слагаемое со знаком "-", слагаемое со знаком "+".

Мнемоническое правило вычисления определителя третьего порядка:

слагаемые со знаком "+", слагаемые со знаком "-".

Можно построить мнемонические правила для вычисления определителей порядка выше чем три, но они будут слишком громоздкими. Поэтому вычисление таких определителей основано на свойствах определителей.

Свойства определителей

 

Теорема 1. При транспонировании величина определителя не меняется.

Следствие. Строки и столбцы в определителе равноправны, т.е. свойства, справедливые для строк, будут справедливы и для столбцов.

Теорема 2. Если все элементы одной строки определителя умножить на одно и то же число, то и весь определитель умножится на это число.

Следствие. Постоянный множитель строки можно выносить за знак определителя.

Теорема 3. Если в определителе поменять местами две строки, то определитель сменит знак на противоположный.

Следствие 1. Определитель, у которого две строки равны, равен нулю.

Следствие 2. Если в определителе две строки пропорциональны, то такой определитель равен нулю.

Теорема 4. Если строка определителя представлена в виде алгебраической суммы нескольких слагаемых, то определитель равен алгебраической сумме определителей, у которых в первом определителе в данной строке стоит первое слагаемое, во втором - второе слагаемое и т.д.

Следствие. Если строки определителя линейно зависимы, то такой определитель равен нулю.

Теорема 5. Если к элементам одной строки определителя прибавить соответствующие элементы другой, умноженные на одно и то же число, то определитель не изменится.

 

9) Миноры и алгебраические дополнения.

Пусть дана прямоугольная матрица А размера .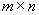

Определение 1. Минором порядка k данной матрицы, где k 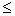min(m;n), называется определитель k-го порядка, полученный из матрицы А вычеркиванием (m - k) строк и (n - k) столбцов.

Определение 2. Дополнительным минором Mij к элементу aij квадратной матрицы 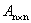называется определитель (n-1) порядка, полученный из матрицы А вычеркиванием этого элемента вместе со строкой и столбцом, в которых он расположен.

Определение 3. Алгебраическим дополнением Aij к элементу aij квадратной матрицы 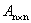называется число Aij= .

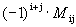Теорема 1. Определитель равен сумме попарных произведений элементов любой строки на их алгебраические дополнения.

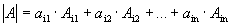- разложение определителя по i-й строке.

Теорема 2. Сумма попарных произведений элементов любой строки определителя на алгебраические дополнения к соответствующим элементам другой строки равна нулю.

Вычисление определителей порядка n>3 сводится к вычислению определителей второго и третьего порядка с помощью теоремы 1 и свойства 5 определителя.

Перед разложением определителя для удобства получают в одном из столбцов нули. Это сокращает объемы вычислений. Для этого используют пятое свойство определителя. Одну из строк умножают на некоторые числа и складывают с другими строками.

10) Обратная матрица. Единственность.

Определение 1. Квадратная матрица называется вырожденной, если ее определитель равен нулю, и невырожденной - в противном случае.

Определение 2. Матрица А-1 называется обратной к квадратной матрице А n-го порядка, если А·А-1= А-1·А=Е.

Теорема 1. Для любой невырожденной квадратной матрицы существует единственная обратная матрица.

Доказательство. 1 часть (единственность).

Предположим, что обратная матрица существует. Докажем, что она единственная. Предположим противное, т.е. существует две обратные матрицы: А-1 и .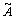

Тогда А·А-1=А-1·А=Е и А· 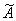= 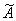·А=Е.

Рассмотрим равенство

А·А-1=Е.

Умножим его слева на .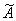

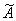·А·А-1= 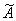·Е,

Е·А-1= ,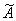

А-1= .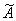

Получили противоречие.

11) Обратная матрица. Существование.


Определение 1. Квадратная матрица называется вырожденной, если ее определитель равен нулю, и невырожденной - в противном случае.

Определение 2. Матрица А-1 называется обратной к квадратной матрице А n-го порядка, если А·А-1= А-1·А=Е.

Теорема 1. Для любой невырожденной квадратной матрицы существует единственная обратная матрица.

2 часть (существование). Дана матрица

А = , .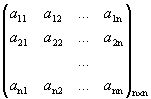

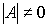Построим обратную матрицу. Для этого совершим ряд действий:

1) заменим все элементы матрицы их алгебраическими дополнениями:

А* 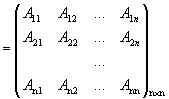- матрица, присоединенная к матрице А;

2) транспонируем полученную матрицу:

(А*)Т= ;

3) разделим все элементы на число ½А½

.

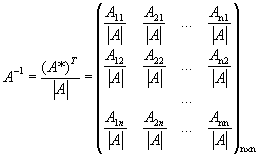Проверим, будет ли полученная матрица обратной к исходной. Для этого умножим матрицу А на А-1. Элемент, стоящий в i-й строке и j-м столбце матрицы произведения, будет равен

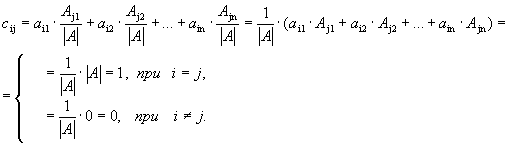
Элементы матрицы-результата совпадают с элементами единичной матрицы Е. Следовательно, А · А-1=Е, т.е. А-1 - обратная матрица к А.

12) Элементарные преобразования над матрицей. Второй способ нахождения обратной матрицы.

Определение 1. Элементарными преобразованиями над матрицей называются:

1) умножение любой строки на число, отличное от нуля;

2) прибавление к элементам одной строки соответствующих элементов другой, умноженных на одно и то же число;

3) перестановка строк;

4) отбрасывание строки из нулей.

Определение 2. Две матрицы называются эквивалентными (А~В), если от одной можно перейти к другой с помощью конечного числа элементарных преобразований.

Теорема. Любую невырожденную квадратную матрицу с помощью элементарных преобразований можно привести к единичной матрице того же порядка. Применяя ту же последовательность элементарных преобразований к единичной матрице, можно получить обратную матрицу к данной.

Обычно элементарные преобразования производят над данной матрицей и единичной одновременно. Для этого составляют расширенную матрицу, в левой части которой стоит исходная матрица, а в правой - единичная матрица того же порядка. С помощью элементарных преобразований в левой части создают единичную матрицу, параллельно в правой части автоматически создается обратная матрица.

.

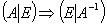13. Ранг матрицы.

Пусть дана произвольная матрица размером 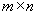. Возьмем произвольные k строк и k столбцов, 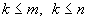. Минором порядка k называют определитель порядка k , составленный из элементов, расположенных на пересечении выбранных k строк и k столбцов, и обозначают Mk.