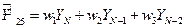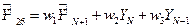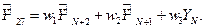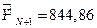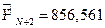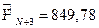Задача 8 (Тема 11)
Значения спроса на продукцию фирмы за каждый месяц в течение двух лет приведены в таблице 10. Требуется построить прогноз спроса для первых трех месяцев следующего года методом скользящего среднего (при этом необходимо определить оптимальные весовые коэффициенты и их количество).
Таблица 10
| Месяцы | Спрос | |||||||||
| Номер варианта | ||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 | 528 | 429 | 594 | 396 | 792 | 561 | 726 | 858 | 363 | 891 |
| 2 | 608 | 494 | 684 | 456 | 912 | 646 | 836 | 988 | 418 | 1026 |
| 3 | 496 | 403 | 558 | 372 | 744 | 527 | 682 | 806 | 341 | 837 |
| 4 | 560 | 455 | 630 | 420 | 840 | 595 | 770 | 910 | 385 | 945 |
| 5 | 480 | 390 | 540 | 360 | 720 | 510 | 660 | 780 | 330 | 810 |
| 6 | 576 | 468 | 648 | 432 | 864 | 612 | 792 | 936 | 396 | 972 |
| 7 | 544 | 442 | 612 | 408 | 816 | 578 | 748 | 884 | 374 | 918 |
| 8 | 624 | 507 | 702 | 468 | 936 | 663 | 858 | 1014 | 429 | 1053 |
| 9 | 624 | 507 | 702 | 468 | 936 | 663 | 858 | 1014 | 429 | 1053 |
| 10 | 576 | 468 | 648 | 432 | 864 | 612 | 792 | 936 | 396 | 972 |
| 11 | 640 | 520 | 720 | 480 | 960 | 680 | 880 | 1040 | 440 | 1080 |
| 12 | 608 | 494 | 684 | 456 | 912 | 646 | 836 | 988 | 418 | 1026 |
| 13 | 592 | 481 | 666 | 444 | 888 | 629 | 814 | 962 | 407 | 999 |
| 14 | 624 | 507 | 702 | 468 | 936 | 663 | 858 | 1014 | 429 | 1053 |
| 15 | 512 | 416 | 576 | 384 | 768 | 544 | 704 | 832 | 352 | 864 |
| 16 | 608 | 494 | 684 | 456 | 912 | 646 | 836 | 988 | 418 | 1026 |
| 17 | 592 | 481 | 666 | 444 | 888 | 629 | 814 | 962 | 407 | 999 |
| 18 | 624 | 507 | 702 | 468 | 936 | 663 | 858 | 1014 | 429 | 1053 |
| 19 | 592 | 481 | 666 | 444 | 888 | 629 | 814 | 962 | 407 | 999 |
| 20 | 560 | 455 | 630 | 420 | 840 | 595 | 770 | 910 | 385 | 945 |
| 21 | 592 | 481 | 666 | 444 | 888 | 629 | 814 | 962 | 407 | 999 |
| 22 | 544 | 442 | 612 | 408 | 816 | 578 | 748 | 884 | 374 | 918 |
| 23 | 560 | 455 | 630 | 420 | 840 | 595 | 770 | 910 | 385 | 945 |
| 24 | 576 | 468 | 648 | 432 | 864 | 612 | 792 | 936 | 396 | 972 |
Решение
Пусть  – число наблюдений,
– число наблюдений,  – реальные значения спроса.
– реальные значения спроса.
Согласно методу скользящих средних прогнозные значения спроса 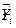 (при
(при 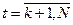 ) вычисляются по формуле:
) вычисляются по формуле: 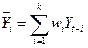 , где
, где 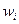 – весовые коэффициенты,
– весовые коэффициенты, 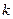 – их количество.
– их количество.
В качестве оценки точности прогноза будем использовать среднеквадратичное отклонение прогнозных значений от реальных: 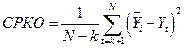 .
.
Таким образом, для нахождения весовых коэффициентов 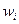 решается следующая задача:
решается следующая задача:
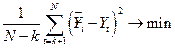 ,
,
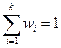 ,
,
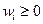 ,
, 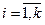 .
.
(При этом 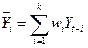 .)
.)
Указанную выше оптимизационную задачу удобно решать в Excel с помощью модуля «Поиск решения». «Поиск решения» находится в меню «Сервис».
Пусть, например, при 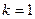
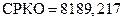 (при этом
(при этом 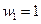 );
);
при 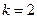 минимальное значение СРКО равно
минимальное значение СРКО равно 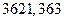 (при этом
(при этом 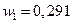 ,
, 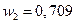 );
);
при 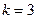 минимальное значение
минимальное значение 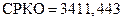 (при этом
(при этом 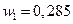 ,
, 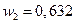 ,
, 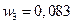 ) ;
) ;
при 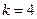 минимальное значение
минимальное значение 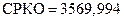 (при этом
(при этом 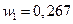 ,
, 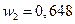 ,
, 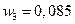 ,
, 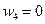 ) .
) .
Заметим, что минимальное значение показателя 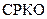 равно
равно 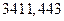 при
при 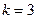 .
.
Следовательно, оптимальное количество весовых коэффициентов равно 3, и при этом 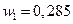 ,
, 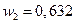 ,
, 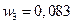 .
.
Для первых трех месяцев следующего года прогнозные значения спроса находятся следующим образом: