Задача 7 (Тема 8)
Данные о рыночной цене коттеджей (которые строит фирма), а также об их площади, вместимости гаража и количестве комнат приведены в таблицах 7, 8 и 9.
Требуется:
1) построить линейную регрессионную модель для оценки рыночной стоимости коттеджей, и с помощью этой модели оценить рыночную стоимость коттеджа с 4 комнатами, площадью 200 кв.м., и с вместимостью гаража – 1 автомобиль;
2) с помощью t-статистик проверить гипотезы о незначимости каждого в отдельности объясняющего фактора при уровне значимости 0,1.
3) С помощью F-статистики проверить гипотезу о незначимости всех объясняющих факторов одновременно при уровне значимости 0,1.
4) Выбрать объясняющие факторы, обеспечивающие наибольшее значение скорректированного коэффициента детерминации и с помощью соответствующей модели оценить рыночную стоимость коттеджа с характеристиками, приведенными в п.1.
Таблица 7
| Номер наблюдения | Цена, ден.ед. | |||||||||
| Номер варианта | ||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 | 150995 | 146510 | 152490 | 167440 | 161460 | 173420 | 168935 | 159965 | 153985 | 174915 |
| 2 | 169579 | 164542 | 171258 | 188048 | 181332 | 194764 | 189727 | 179653 | 172937 | 196443 |
| 3 | 197455 | 191590 | 199410 | 218960 | 211140 | 226780 | 220915 | 209185 | 201365 | 228735 |
| 4 | 202101 | 196098 | 204102 | 224112 | 216108 | 232116 | 226113 | 214107 | 206103 | 234117 |
| 5 | 227654 | 220892 | 229908 | 252448 | 243432 | 261464 | 254702 | 241178 | 232162 | 263718 |
| 6 | 243915 | 236670 | 246330 | 270480 | 260820 | 280140 | 272895 | 258405 | 248745 | 282555 |
| 7 | 220685 | 214130 | 222870 | 244720 | 235980 | 253460 | 246905 | 233795 | 225055 | 255645 |
| 8 | 290375 | 281750 | 293250 | 322000 | 310500 | 333500 | 324875 | 307625 | 296125 | 336375 |
| 9 | 290375 | 281750 | 293250 | 322000 | 310500 | 333500 | 324875 | 307625 | 296125 | 336375 |
| 10 | 318251 | 308798 | 321402 | 352912 | 340308 | 365516 | 356063 | 337157 | 324553 | 368667 |
| 11 | 348450 | 338100 | 351900 | 386400 | 372600 | 400200 | 389850 | 369150 | 355350 | 403650 |
Таблица 8
| Номер наблю-дения | Площадь, кв.м. | |||||||||
| Номер варианта | ||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 | 101 | 98 | 102 | 112 | 108 | 116 | 113 | 107 | 103 | 117 |
| 2 | 111,1 | 107,8 | 112,2 | 123,2 | 118,8 | 127,6 | 124,3 | 117,7 | 113,3 | 128,7 |
| 3 | 116,15 | 112,7 | 117,3 | 128,8 | 124,2 | 133,4 | 129,95 | 123,05 | 118,45 | 134,55 |
| 4 | 141,4 | 137,2 | 142,8 | 156,8 | 151,2 | 162,4 | 158,2 | 149,8 | 144,2 | 163,8 |
| 5 | 171,7 | 166,6 | 173,4 | 190,4 | 183,6 | 197,2 | 192,1 | 181,9 | 175,1 | 198,9 |
| 6 | 181,8 | 176,4 | 183,6 | 201,6 | 194,4 | 208,8 | 203,4 | 192,6 | 185,4 | 210,6 |
| 7 | 191,9 | 186,2 | 193,8 | 212,8 | 205,2 | 220,4 | 214,7 | 203,3 | 195,7 | 222,3 |
| 8 | 191,9 | 186,2 | 193,8 | 212,8 | 205,2 | 220,4 | 214,7 | 203,3 | 195,7 | 222,3 |
| 9 | 212,1 | 205,8 | 214,2 | 235,2 | 226,8 | 243,6 | 237,3 | 224,7 | 216,3 | 245,7 |
| 10 | 212,1 | 205,8 | 214,2 | 235,2 | 226,8 | 243,6 | 237,3 | 224,7 | 216,3 | 245,7 |
| 11 | 232,3 | 225,4 | 234,6 | 257,6 | 248,4 | 266,8 | 259,9 | 246,1 | 236,9 | 269,1 |
Таблица 9
| Номер наблюдения | Вместимость гаража | К-во комнат |
| 1 | 0 | 3 |
| 2 | 0 | 3 |
| 3 | 1 | 3 |
| 4 | 0 | 4 |
| 5 | 1 | 4 |
| 6 | 1 | 5 |
| 7 | 0 | 4 |
| 8 | 1 | 5 |
| 9 | 2 | 5 |
| 10 | 2 | 5 |
| 11 | 2 | 5 |
Решение
Пусть 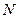 – число наблюдений,
– число наблюдений, 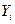 – цена коттеджа для наблюдения
– цена коттеджа для наблюдения 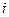 ,
, 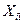 ,
, 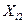 ,
, 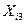 – площадь, вместимость гаража и количество комнат для наблюдения
– площадь, вместимость гаража и количество комнат для наблюдения 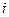 .
.
Прогнозные значения 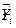 (при
(при 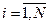 ) находятся по формуле:
) находятся по формуле: 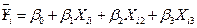 , где
, где 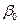 ,
, 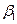 ,
, 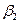 и
и 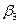 – параметры.
– параметры.
В качестве оценки точности прогноза используется сумма квадратов отклонений прогнозных значений от реальных: 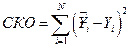 .
.
Для нахождения значений параметров 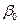 ,
, 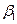 ,
, 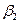 и
и 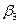 минимизируется
минимизируется 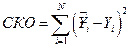 .
.
Оценка 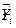 рыночной стоимости коттеджа при известных значениях показателей
рыночной стоимости коттеджа при известных значениях показателей 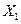 ,
, 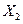 и
и 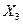 производится по формуле:
производится по формуле: 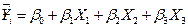 .
.
Требуется:
1) построим линейную регрессионную модель для оценки рыночной стоимости коттеджей, и с помощью этой модели оценим рыночную стоимость коттеджа с 4 комнатами, площадью 200 кв.м., и с вместимостью гаража – 1 автомобиль;
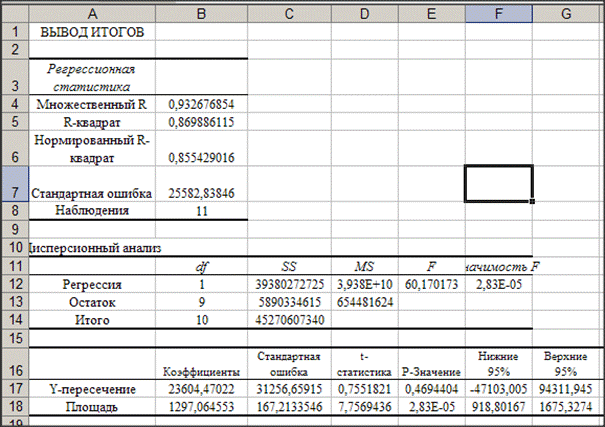
При выполнении задачи в Excel следует использовать модуль «Регрессия» в «Анализе данных». «Анализ данных» находится в меню «Сервис».
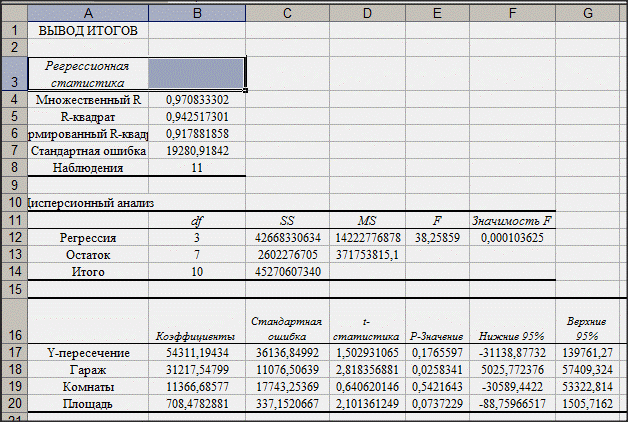
Получили уравнение регрессии:
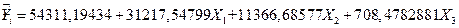
Оценим рыночную стоимость коттеджа с 4 комнатами, площадью 200 кв.м., и с вместимостью гаража – 1 автомобиль:
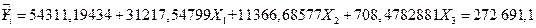 ден. ед.
ден. ед.
2) с помощью t-статистик проверить гипотезы о незначимости каждого в отдельности объясняющего фактора при уровне значимости 0,1.
Случайная величина 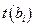 имеет распределение Стьюдента со степенями свободы
имеет распределение Стьюдента со степенями свободы 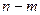 :
: 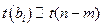
Статистики 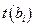 можно использовать для проверки гипотез.
можно использовать для проверки гипотез.
Пусть 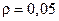 .В условиях нашего примера
.В условиях нашего примера 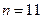 ,
, 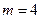 и
и 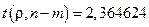 .
.
Как видно из таблицы, значимым коэффициентом является только 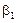 , все остальные факторы – незначимы.
, все остальные факторы – незначимы.
3) С помощью F-статистики проверить гипотезу о незначимости всех объясняющих факторов одновременно при уровне значимости 0,1.
В случае, если 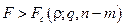 нулевая гипотеза отвергается; если
нулевая гипотеза отвергается; если 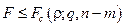 , нет оснований отвергать нулевую гипотезу (и она принимается).
, нет оснований отвергать нулевую гипотезу (и она принимается).
В условиях нашего примера при 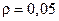 :
:
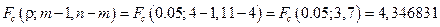
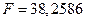 ;
; 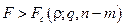 - модель значима.
- модель значима.
4)
Построим Матрицу коэффициентов парной корреляции, используя надстройку MS Excel Пакет анализа (команда Сервис\ Анализ данных\ Корреляция)
Матрица коэффициентов парной корреляции
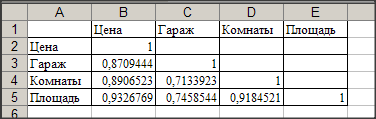
Анализируя матрицу парных коэффициентов корреляции, можно отметить тесную корреляционную связь между переменными Х2 и Х3 ( 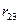 = 0,918452), что, очевидно, свидетельствует о мультиколлинеарности объясняющих переменных.
= 0,918452), что, очевидно, свидетельствует о мультиколлинеарности объясняющих переменных.
Для устранения мультиколлинеарности применим процедуру пошагового отбора наиболее информативных переменных.
Из объясняющих переменных Х1—Х3 выделяется переменная Х3, имеющая с зависимой переменной Y наибольший коэффициент детерминации 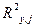 (равный для парной модели квадрату коэффициента корреляции
(равный для парной модели квадрату коэффициента корреляции 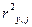 ). Очевидно, это переменная Х3, так как коэффициент детерминации
). Очевидно, это переменная Х3, так как коэффициент детерминации 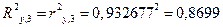 — максимальный.
— максимальный.
С учетом поправки на несмещенность по формуле –
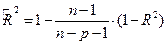
скорректированный коэффициент детерминации
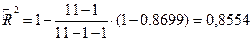
Среди всевозможных пар объясняющих переменных Х3, 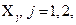 выбирается пара (Х3, Х2), имеющая с зависимой переменной Y наиболее высокий коэффициент детерминации
выбирается пара (Х3, Х2), имеющая с зависимой переменной Y наиболее высокий коэффициент детерминации 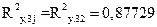 и с учетом поправки
и с учетом поправки
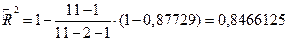
Так как скорректированный коэффициент детерминации на 2-м шаге не увеличился, то в регрессионной модели достаточно ограничиться лишь одной отобранной ранее объясняющей переменной Х3.
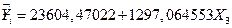
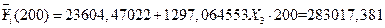 ден. ед.
ден. ед.








