Задача 5 (Тема 5)
Осуществление проекта требует выполнения ряда работ. Номера работ, их продолжительности и перечни работ, которые должны быть закончены к началу выполнения других работ, приведены в табл. 5.
Требуется:
1) построить сетевой график выполнения работ;
2) рассчитать минимальное время выполнения всего комплекса работ;
3) определить ранние и поздние сроки начала и окончания работ, и их полные и свободные резервы времени;
4) найти критические работы и построить критический путь (на сетевом графике).
Таблица 5
| Номера работ | Предше-ствующие работы | Продолжительность работы, дн. | |||||||||
| Номер варианта | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 1 | – | 65 | 15 | 45 | 60 | 35 | 40 | 10 | 20 | 30 | 55 |
| 2 | – | 39 | 9 | 27 | 36 | 21 | 24 | 6 | 12 | 18 | 33 |
| 3 | 1 | 91 | 21 | 63 | 84 | 49 | 56 | 14 | 28 | 42 | 77 |
| 4 | 1 | 78 | 18 | 54 | 72 | 42 | 48 | 12 | 24 | 36 | 66 |
| 5 | 2 | 91 | 21 | 63 | 84 | 49 | 56 | 14 | 28 | 42 | 77 |
| 6 | 4, 5 | 39 | 9 | 27 | 36 | 21 | 24 | 6 | 12 | 18 | 33 |
| 7 | 4, 5 | 130 | 30 | 90 | 120 | 70 | 80 | 20 | 40 | 60 | 110 |
| 8 | 3, 6 | 104 | 24 | 72 | 96 | 56 | 64 | 16 | 32 | 48 | 88 |
Решение
Дугам (стрелкам) сетевого графика соответствуют работы, а вершинам – события. Событие заключается в окончании выполнения работ, в него входящим, а также в начале выполнения работ, из него выходящих.
Для нахождения минимального времени выполнения всего комплекса работ и временных характеристик работ нужно вначале рассчитать характеристики событий.
Ранние сроки свершения событий рассчитываются по формуле:
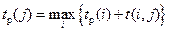 ,
,
где 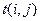 – продолжительность работы
– продолжительность работы 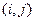 , а максимум берется по всем событиям
, а максимум берется по всем событиям 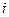 , непосредственно предшествующим событию
, непосредственно предшествующим событию 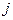 .
.
При этом ранний срок свершения начального события полагается равным нулю: 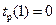 .
.
Поздние сроки свершения событий рассчитываются по формуле:
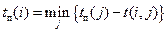 ,
,
где максимум берется по всем событиям 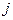 , непосредственно следующим за событием
, непосредственно следующим за событием 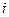 .
.
При этом поздний срок свершения завершающего события полагается равным раннему сроку свершения этого события.
Резервы времени событий рассчитываются по формуле:
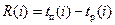 .
.
Описанные выше характеристики событий удобно находить на сетевом графике. Для этого необходимо события изобразить кружками, разделенными на четыре сектора. В верхнем секторе указывается номер события, в левом и правом – ранний и поздний сроки свершения этого события, в нижнем – его резерв времени:
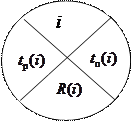 |
Продолжительности выполнения работ указываются возле соответствующих дуг сетевого графика.
Расчет характеристик событий на сетевом графике начинается с внесения раннего срока 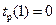 свершения начального события в левый сектор соответствующего кружка. Затем находятся ранние сроки остальных событий. При этом нужно двигаться слева направо от более ранних событий к более поздним. Поздний срок свершения завершающего события полагается равным раннему сроку свершения этого события. Для расчета поздних сроков свершения событий нужно двигаться справа налево от более поздних событий к более ранним.
свершения начального события в левый сектор соответствующего кружка. Затем находятся ранние сроки остальных событий. При этом нужно двигаться слева направо от более ранних событий к более поздним. Поздний срок свершения завершающего события полагается равным раннему сроку свершения этого события. Для расчета поздних сроков свершения событий нужно двигаться справа налево от более поздних событий к более ранним.
После расчета ранних и поздних сроков свершения событий находятся резервы времени событий по указанной выше формуле.
Минимальное время выполнения комплекса работ равно раннему сроку свершения завершающего события.
Работы, соединяющие события с нулевым резервом времени, являются критическими (т.е. любая задержка выполнения этих работ приводит к увеличению времени выполнения всего комплекса работ).
Ранние и поздние сроки начала и окончания работ, и их полные и свободные резервы времени находят (с помощью уже найденных ранних и поздних сроков свершения событий, и заданных продолжительностей выполнения работ) по следующим формулам:
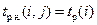 ,
,
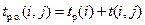 ,
,
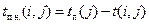 ,
,
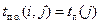 ,
,
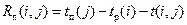 ,
,
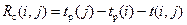 .
.
Критические работы – это работы, полный резерв времени которых равен нулю.
Критический путь – это путь, состоящий из критических работ, который соединяет начальное и конечное события.
Рассчитаем характеристики событий четырёхсекторным методом.
Вычисляем ранний срок свершения каждого события –
tр(1)=0,
tР(2) =0+35 =35,
tp(3) = 0+21=21,
tp(4) = max (35+42; 21+49) = 77
tp(5) = max (35+49; 77+21) = 98
tp(6) = max (98+56; 77+70) = 154
Заносим вычисленные значения в левые секторы. Далее считаем поздние сроки свершения событий.
Полагая tП(6) = tр(6) = 154 дн., перемещаемся в обратном направлении от события №6 к событию №1 и получаем –
tП(5) = 154-56=98
tП(4) = min {154-70; 98-21} = 77
tП(3) = 77-49=28
tП(2) = min {98-49; 77-42} = 35
tП(l) = min {35-35; 28-21} = 0.
Заносим вычисленные значения в правые секторы.
Резерв времени событий вычисляем в любом порядке, вычитая из правого сектора левый сектор. Значение записываем в нижний сектор. В нашем случае
R(1) = R(2) = R(4) = R(5) = R(6) = 0,
то есть не все события имеют нулевой резерв времени.
Так как tП(6) = tp(6) = tKp = 154 дн., то весь комплекс работ может быть выполнен за минимальный срок 154 дн.
Вычисляем полные резервы времени работ – 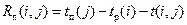
то есть отнимаем от позднего срока свершения конечного события j ранний срок свершения начального события % и длительность работы.
Имеем:
RП (1,2) = tП(2) – tp(1) – t(1,2)= 35-0-35=0
RП (1,3) = tП(3) – tp(1) – t(1,3)= 28-0-21=7
RП (2,5) = tП(5) – tp(2) – t(2,5)= 98-35-49=14
RП (2,4) = tП(4) – tp(2) – t(2,4)= 77-35-42=0
RП (3,4) = tП(4) – tp(3) – t(3,4)= 77-21-49=7
RП (4,5) = tП(5) – tp(4) – t(4,5)= 98-77-21=0
RП (4,6) = tП(6) – tp(4) – t(4,6)= 154-77-70=7
RП (5,6) = tП(6) – tp(5) – t(5,6)= 154-98-56=0
Работы (1,2), (2,4), (4,5) и (5,6) имеют нулевой резерв времени и являются критическими. Срыв сроков их выполнения сразу же приводит к увеличению времени выполнения всего комплекса работ.
Вычисляем свободные резервы времени работ – 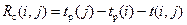
то есть отнимаем от раннего срока свершения конечного события j ранний срок свершения начального события % и длительность работы.
Имеем:
Rс (1,2) = tр(2) – tp(1) – t(1,2)= 35-0-35=0
Rс (1,3) = tр(3) – tp(1) – t(1,3)= 21-0-21=0
Rс (2,5) = tр(5) – tp(2) – t(2,5)= 98-35-49=14
Rс (2,4) = tр(4) – tp(2) – t(2,4)= 77-35-42=0
Rс (3,4) = tр(4) – tp(3) – t(3,4)= 77-21-49=7
Rс (4,5) = tр(5) – tp(4) – t(4,5)= 98-77-21=0
Rс (4,6) = tр(6) – tp(4) – t(4,6)= 154-77-70=7
Rс (5,6) = tр(6) – tp(5) – t(5,6)= 154-98-56=0
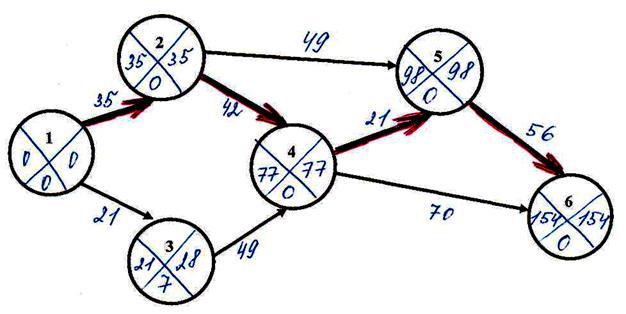
Построим критический путь. Для этого выделим на сетевом графике критические работы. Они составляют критический путь.
|
|
Рис. 5.1. Сетевой график с характеристиками событий