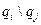Задача 4 (Тема 4)
Издержки фирмы на производство продукции составляют 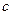 денежных единиц в расчете на 1 единицу продукции.
денежных единиц в расчете на 1 единицу продукции.
Фирма реализует продукцию по цене 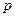 ден.ед. Непроданный товар реализуется по сниженной цене, равной
ден.ед. Непроданный товар реализуется по сниженной цене, равной 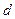 ден.ед.
ден.ед.
Спрос может составлять 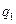 ,
, 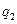 ,
, 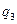 и
и 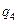 шт. Определить оптимальное количество производимой продукции с помощью критериев Лапласа, Вальда, Сэвиджа и Гурвица (при заданном значении параметра
шт. Определить оптимальное количество производимой продукции с помощью критериев Лапласа, Вальда, Сэвиджа и Гурвица (при заданном значении параметра 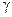 ).
).
Значения параметров 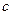 ,
, 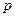 ,
, 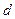 ,
, 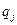 (где
(где 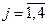 ) и
) и 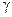 приведены в табл. 4.
приведены в табл. 4.
Таблица 4
| Параметры | Номер варианта | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|
| 17 | 14 | 12 | 18 | 23 | 29 | 27 | 16 | 8 | 11 |
|
| 25,5 | 21 | 18 | 27 | 34,5 | 43,5 | 40,5 | 24 | 12 | 16,5 |
|
| 15,3 | 12,6 | 10,8 | 16,2 | 20,7 | 26,1 | 24,3 | 14,4 | 7,2 | 9,9 |
|
| 340 | 280 | 240 | 360 | 460 | 580 | 540 | 320 | 160 | 220 |
|
| 425 | 350 | 300 | 450 | 575 | 725 | 675 | 400 | 200 | 275 |
|
| 510 | 420 | 360 | 540 | 690 | 870 | 810 | 480 | 240 | 330 |
|
| 595 | 490 | 420 | 630 | 805 | 1015 | 945 | 560 | 280 | 385 |
| γ | 0,51 | 0,42 | 0,36 | 0,54 | 0,69 | 0,87 | 0,81 | 0,48 | 0,24 | 0,34 |
Решение
Используем обозначения:
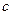 – стоимость производства единицы продукции,
– стоимость производства единицы продукции, 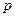 – цена реализации,
– цена реализации, 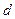 – сниженная цена,
– сниженная цена, 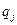 – значение спроса (
– значение спроса ( 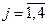 ).
).
Обозначим через 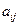 прибыль фирмы в случае, когда производимое количество товара равно
прибыль фирмы в случае, когда производимое количество товара равно 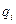 , а спрос равен
, а спрос равен 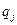 .
.
Вычислим значения 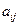 по формуле:
по формуле:
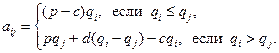
Пусть, например, 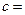 23,
23, 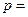 34,5,
34,5, 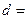 20.7,
20.7, 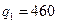 ,
, 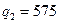 ,
, 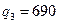 ,
, 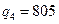 .
.
Тогда платежная матрица 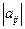 имеет вид:
имеет вид:
|
| 460 | 575 | 690 | 805 |
| 460 | 5290 | 5290 | 5290 | 5290 |
| 575 | 5025,5 | 6612,5 | 6612,5 | 6612,5 |
| 690 | 4761 | 6348 | 7935 | 7935 |
| 805 | 4496,5 | 6083,5 | 7670,5 | 9257,5 |
Критерий Лапласа
Найдем среднюю прибыль фирмы 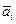 при производимом количестве
при производимом количестве 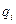 по формуле:
по формуле:
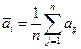
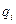
|
|
| 460 | 5290 |
| 575 | 6215,75 |
| 690 | 6744,75 |
| 805 | 6877 |
Заметим, что максимальное значение 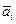 достигается при
достигается при 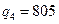 . Следовательно, оптимальной по Лапласу будет стратегия фирмы, состоящая в производстве 805 ед.товара.
. Следовательно, оптимальной по Лапласу будет стратегия фирмы, состоящая в производстве 805 ед.товара.
Критерий Вальда
Найдем наименьшую прибыль фирмы при производимом количестве 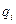 :
:
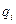
|
|
| 460 | 5290 |
| 575 | 5025,5 |
| 690 | 4761 |
| 805 | 4496,5 |
Заметим, что максимальное значение 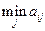 достигается при
достигается при 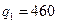 . Следовательно, оптимальной по Вальду будет стратегия фирмы, состоящая в производстве 460 ед.товара.
. Следовательно, оптимальной по Вальду будет стратегия фирмы, состоящая в производстве 460 ед.товара.
Критерий Сэвиджа
Найдем риски 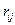 по формуле:
по формуле: 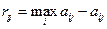 .
.
|
| 460 | 575 | 690 | 805 |
| 460 | 0 | 1322,5 | 2645 | 3967,5 |
| 575 | 264,5 | 0 | 1322,5 | 2645 |
| 690 | 529 | 264,5 | 0 | 1322,5 |
| 805 | 793,5 | 529 | 264,5 | 0 |
Найдем максимальные риски при производимых количествах 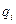 :
:
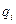
|
|
| 460 | 3967,5 |
| 575 | 2645 |
| 690 | 1322,5 |
| 805 | 793,5 |
Заметим, что минимальное значение 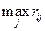 достигается при
достигается при 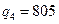 .
.
Следовательно, оптимальной по Сэвиджу будет стратегия фирмы, состоящая в производстве 805 ед.товара.
Критерий Гурвица
Вычислим значения 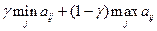 . Например, при
. Например, при 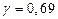 , эти значения равны:
, эти значения равны:
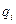
|
|
| 460 | 5290 |
| 575 | 5517,47 |
| 690 | 5744,94 |
| 805 | 5972,41 |
Заметим, что максимальное значение 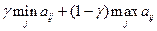 достигается при
достигается при 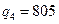 .
.
Следовательно, оптимальной по Гурвицу (при 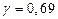 ) будет стратегия фирмы, состоящая в производстве 805 ед.товара.
) будет стратегия фирмы, состоящая в производстве 805 ед.товара.