Задача 3 (Тема 3)
Распределение спроса на используемую фирмой продукцию за время выполнения заказа дискретно и задано в табл. 3.
Продукция поставляется в среднем один раз в 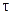 дней, издержки хранения одной единицы продукции в течение одного дня составляют
дней, издержки хранения одной единицы продукции в течение одного дня составляют 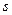 ден.ед., а издержки, связанные с дефицитом одной единицы продукции, равны
ден.ед., а издержки, связанные с дефицитом одной единицы продукции, равны 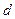 ден.ед.
ден.ед.
Требуется определить оптимальные страховой запас и точку размещения заказа (при которых суммарные издержки, связанные с содержанием страхового запаса и с дефицитом, минимальны), а также средний уровень дефицита, издержки содержания страхового запаса и потери, связанные с дефицитом (при найденных оптимальных страховом запасе и точке размещения заказа).
Значения параметров 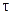 ,
, 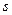 и
и 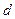 приведены в табл. 4.
приведены в табл. 4.
Таблица 3
| Спрос (в единицах продукции) | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
| Вероятность | 0,05 | 0,1 | 0,2 | 0,3 | 0,2 | 0,1 | 0,05 |
Таблица 4
| Параметры | Номер варианта | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|
| 12 | 28 | 24 | 14 | 18 | 36 | 34 | 26 | 16 | 22 |
|
| 0,33 | 0,36 | 0,25 | 1,14 | 1,22 | 0,50 | 0,24 | 0,77 | 0,88 | 0,55 |
|
| 20 | 50 | 30 | 80 | 110 | 90 | 40 | 100 | 70 | 60 |
Решение
Будем использовать следующие обозначения:
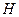 – спрос за время выполнения заказа,
– спрос за время выполнения заказа, 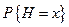 – вероятность того, что спрос за время выполнения заказа составит
– вероятность того, что спрос за время выполнения заказа составит 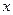 единиц продукции,
единиц продукции,
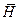 – средний спрос за время выполнения заказа,
– средний спрос за время выполнения заказа, 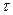 – среднее количество дней между очередными поставками,
– среднее количество дней между очередными поставками, 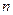 – среднее количество поставок в голу,
– среднее количество поставок в голу, 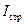 – страховой запас,
– страховой запас, 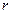 – точка размещения заказа,
– точка размещения заказа, 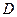 – уровень дефицита,
– уровень дефицита, 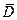 – средний уровень дефицита,
– средний уровень дефицита, 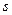 – издержки хранения единицы продукции в течение одного дня,
– издержки хранения единицы продукции в течение одного дня, 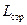 – годовые издержки содержания страхового запаса,
– годовые издержки содержания страхового запаса, 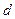 – издержки, связанные с дефицитом единицы продукции,
– издержки, связанные с дефицитом единицы продукции, 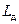 – годовые издержки, связанные с дефицитом,
– годовые издержки, связанные с дефицитом, 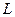 – суммарные издержки, связанные с содержанием страхового запаса и с дефицитом
– суммарные издержки, связанные с содержанием страхового запаса и с дефицитом
Имеют место следующие равенства:
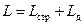 ,
,
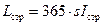 (считая, что количество дней в году – 365)
(считая, что количество дней в году – 365)
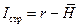 ,
, 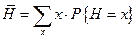
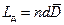 ,
, 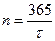 ,
, 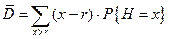
Обозначим через 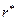 – оптимальную точку размещения заказа, при которой суммарные издержки
– оптимальную точку размещения заказа, при которой суммарные издержки 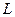 минимальны.
минимальны.
Через 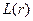 обозначим суммарные издержки при точке размещения заказа, равной
обозначим суммарные издержки при точке размещения заказа, равной 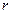 .
.
Для оптимальной точки размещения заказа 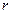 одновременно должны выполняться условия:
одновременно должны выполняться условия:
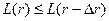 ,
,
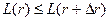 .
.
Используя записанные выше формулы, можно показать, что эти условия равносильны следующим:
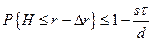 ,
,
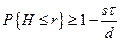 .
.
Пусть, например, 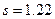 ,
, 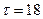 ,
, 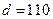 , а распределение спроса задано в следующей таблице:
, а распределение спроса задано в следующей таблице:
Спрос, 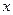
| 15 | 20 | 25 | 30 | 35 | 40 | 45 |
Вероятность, 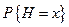
| 0,05 | 0,1 | 0,2 | 0,3 | 0,2 | 0,1 | 0,05 |
Тогда 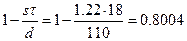 , и записанные выше условия примут вид:
, и записанные выше условия примут вид:
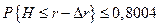 ,
,
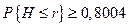 .
.
Добавим в таблицу строку с кумулятивными вероятностями 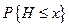
Спрос, 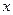
| 15 | 20 | 25 | 30 | 35 | 40 | 45 |
Вероятность, 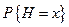
| 0,05 | 0,1 | 0,2 | 0,3 | 0,2 | 0,1 | 0,05 |
Кумулятивная вероятность, 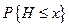
| 0,05 | 0,15 | 0,35 | 0,65 | 0,85 | 0,95 | 1 |
Несложно заметить, что условия 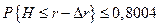 ,
, 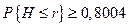 выполняются при
выполняются при 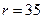 .
.
Следовательно, оптимальная точка размещения заказа равна 35.
По формуле 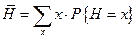 найдем средний спрос за время выполнения заказа:
найдем средний спрос за время выполнения заказа:
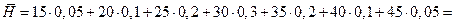 30.
30.
Найдем оптимальный страховой запас: 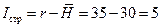 .
.
Средний уровень дефицита найдем по формуле: 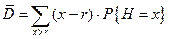
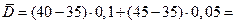 1.
1.
Издержки содержания страхового запаса определяются формулой:
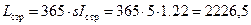 ,
,
а потери, связанные с дефицитом:
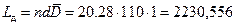 , где
, где 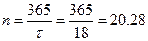 .
.








