Задача 1 (Тема 2)
Фирма принимает заказы по телефону. Если в момент поступления заявки хотя бы один менеджер, принимающий заявки, свободен либо число заявок, ожидающих в очереди, не превосходит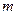 
, заявка принимается. В противном случае заявка теряется. Известно, что в среднем поступает 
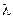звонков в час, среднее время обслуживания одной заявки составляет 
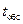минут. Доход, получаемый фирмой в результате обслуживания одной заявки, в среднем равен 
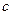ден.ед., а менеджеру по продажам платят 
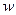ден.ед. в час.
Требуется определить количество менеджеров, при котором прибыль фирмы максимальна.
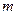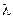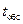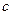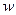Значения параметров , , , и приведены в табл. 1.
Таблица 1
| Параметры | Номер варианта | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|
| 2 | 4 | 3 | 2 | 4 | 2 | 3 | 2 | 3 | 4 |
|
| 44 | 48 | 36 | 56 | 32 | 28 | 52 | 64 | 72 | 68 |
|
| 3,3 | 3,6 | 2,7 | 4,2 | 2,4 | 2,1 | 3,9 | 4,8 | 5,4 | 5,1 |
|
| 5,5 | 6 | 4,5 | 7 | 4 | 3,5 | 6,5 | 8 | 9 | 8,5 |
|
| 3,3 | 3,6 | 2,7 | 4,2 | 2,4 | 2,1 | 3,9 | 4,8 | 5,4 | 5,1 |
Решение
Решим задачу при следующих значениях параметров:
,
,
,
.
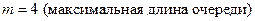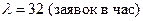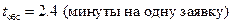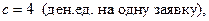
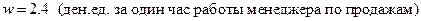Примем час в качестве единицы измерения времени.
Тогда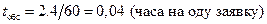 
.
Найдем интенсивность нагрузки: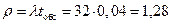 
.
Найдем уровень загрузки системы: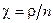 
Прибыль = Доход – Расходы.
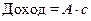, где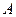 
– абсолютная пропускная способность.
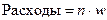, где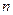 
– число менеджеров по продажам.
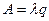, где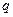 
– относительная пропускная способность.
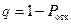, где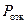 
– вероятность отказа.
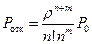, где 
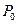– вероятность того, что в системе нет заявок.
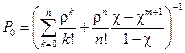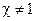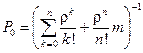при 
.
при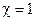 
.
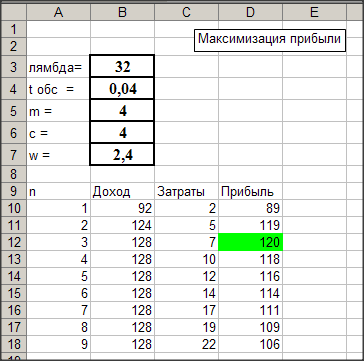
Из приведенных выше формул и расчетов в EXCEL следует, что (при указанных выше значениях параметров) прибыль фирмы равна 89 д.е. при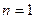 
, 119 д.е. при 
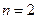, 120 д.е. при 
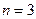и т.д.
Следовательно, прибыль фирмы максимальна при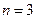 
и равна 120 ден.ед.
Задача 2 (Тема 3)
Фирма использует продукцию пяти видов.
Годовой спрос на товар вида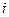 
равен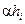 
единиц товара. Издержки размещения заказа и содержания запасов составляют 
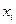и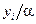 
ден. ед., соответственно. Расход складской площади на единицу товара вида 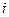равен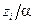 
кв.м. Общая величина площади складских помещений равна 260 кв.м.
Требуется определить оптимальные партии поставок при ограничении на максимальный уровень запаса, а также оценить уменьшение общих расходов на размещение заказов и содержание запасов при увеличении складских помещений на 10 кв.м.
Значения параметров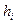 
, , 
, 
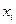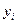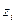. приведены в табл. 2. Значение параметра 
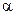определяется формулой: 
.
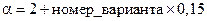Таблица 2
|
|
|
|
|
|
| 1 | 800 | 4 | 16 | 2 |
| 2 | 1600 | 5 | 40 | 3 |
| 3 | 1800 | 6 | 6 | 4 |
| 4 | 1500 | 6 | 20 | 3 |
| 5 | 2000 | 3 | 30 | 1,5 |
Решение
.
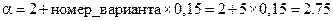Используем обозначения: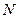 
– количество видов товаров, 
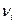– годовой спрос на товар вида , 
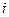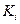– издержки размещения одного заказа (на товар вида ), 
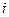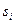– издержки содержания единицы товара вида 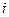в течение года, 
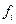– расход складской площади на единицу товара вида , 
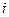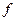– общая площадь торгового зала и складских помещений, 
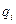– размер партии поставки товара вида .
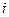Суммарные издержки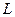 
размещения и содержания в течение года вычисляются по формуле: 
.
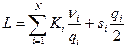Максимальная площадь, необходимая для хранения товарных запасов, равна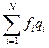 
.
Таким образом, задача минимизации суммарных издержек при ограничении на максимальный уровень запаса имеет вид:
.
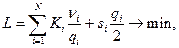
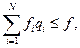
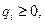
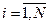Решим задачу при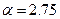 
. Значения всех остальных параметров возьмем из табл.2.
Для решения задачи используем табличный процессор Excel.
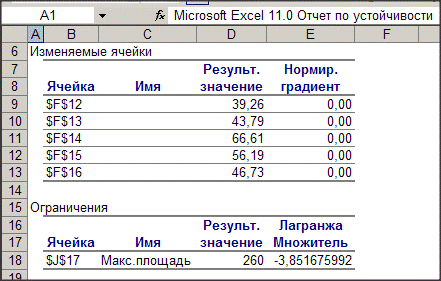
В результате получим: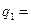 
39.26; 
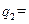43.79; 
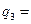66.61; 
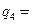56.19; 
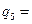46.73.
Множитель Лагража (двойственная оценка ограничения) равен: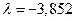 
.
Следовательно, уменьшение общих расходов на размещение заказов и содержание запасов при увеличении складских помещений на 10 кв.м. приблизительно равно:
