13. Кедров-Зихман О.О. Поликросстест в селекции растений. Минск, 1974.
14. Гальперн И.Л. Использование генетико-математического анализа в селекционной работе с птицей бройлерных линий. – Докл. ВАСХНИЛ, № 5, 1973.
15. Котов М.М. Генетика и селекция. Часть 1.: Учебник для вузов. – Йошкар-Ола: МарГТУ, 1997. – 280 с.
16. Любавская А.Я. Лесная селекция и генетика. Учебник для вузов. – М.: Лесная промышленность, 1982. – 288 с.
17. Айала, Ф.Дж. Введение в популяционную и эволюционную генетику / Ф.Дж. Айала / М.: Мир, 1984. – 232 с.
18. Айала, Ф.Дж. Современная генетика / Ф.Дж. Айала, Дж.А. Кайгер /. – В 3-х т. Т. 2. Пер с англ. – М.: Мир, 1988. – 368 с.
19. Гуляев, Г.В. и др. Словарь терминов по генетике, цитологии, селекции, семеноводству и семеноведению /Г.В. Гуляев, В.В. Мальченко. – М.: Россельхозиздат, 1975. – 216 с.
20. Бессчетнова, Н.Н. К вопросу об оценке общей комбинационной способности плюсовых деревьев сосны обыкновенной /Н.Н. Бессчетнова //Вестник московского государственного университета леса – Лесной вестник, № 6. – 2008. – С. 4 – 12.
21. Бессчетнова, Н.Н. Оценка общей комбинационной способности плюсовых деревьев сосны обыкновенной в Нижегородской области /Н.Н. Бессчетнова //Вестник московского государственного университета леса – Лесной вестник, № 4. – 2009. – С. 4 – 10.
22. Бессчетнова, Н.Н. Поликросс-тест в определении оценок общей комбинационной способности сосны обыкновенной /Н.Н. Бессчетнова // Актуальные проблемы лесного комплекса / Под общей редакцией Е.А. Памфилова. // Сборник научных трудов по итогам международной научно-технической конференции. Выпуск 22. – Брянск: БГИТА, 2009. – С. 10 – 14.
23. Бессчетнова, Н.Н. Оценка эффективности отбора плюсовых деревьев сосны обыкновенной в испытательных культурах в Нижегородской области /Н.Н. Бессчетнова //Вестник московского государственного университета леса – Лесной вестник, № 2. – 2009. – С. 31 – 36.
24. Царев, А.П. Селекция и репродукция лесных древесных пород: Учебник/ Под ред. А. П. Царева/ А.П. Царев, С.П. Погиба, В.В. Тренин// Учебник. – М.: Логос, 2003. – 520 с.: ил.
25. Бессчетнова, Н.Н. Сосна обыкновенная (Pinus sylvestris L.). Селекционный потенциал плюсовых деревьев / Н.Н. Бессчетнова. – LAP Lambert Academic Publishing, 2011 – 402 с.
26. Бессчетнов, В.П. Дисперсионный анализ многоуровневых иерархических комплексов. Методические указания для студентов и аспирантов очного и заочного отделений факультета лесного хозяйства по специальности 25020165 - лесное хозяйство / В.П. Бессчетнов, Н.Н. Бессчетнова, О.Ю. Храмова, А.Н. Орнатский, Н.И. Горелов. – Нижний Новгород: Нижегородская государственная сельскохозяйственная академия, 2012. – 33 с.
Асинхронно-синхронная связь с преподавателем:
1. Бессчетнов Владимир Петрович: E-mail: lesfak@bk.ru
Мобильный телефон: 8-906-355-81-97.
2. Бессчетнова Наталья Николаевна: E-mail: besschetnova1966@mail.ru
Мобильный телефон: 8-960-160-54-32.
1. Проблемы генетического анализа в лесной селекции и понятие о комбинационной способности
В лесной селекции проблема выбора наилучших селекционных объектов, отобранных по фенотипу (например, плюсовых деревьев), стоит особенно остро. Она (проблема), прежде всего, инициируется тем, что лесничества и уполномоченные в установленном порядке учреждения и организации в соответствии с действующими нормативами (Указания…, 2000), отбор плюсовых деревьев, ведут по фенотипу, а использовать в дальнейшем селекционном процессе или в хозяйственном плане намереваются лучшие генотипы (элитные деревья). Цель отбора – отбор лучших генотипов. Это предусматривает реализацию такой формы отбора, как индивидуальный отбор. Он (индивидуальный отбор) в лесной селекции воплощается в сравнительную оценку семенных (а иногда еще и вегетативных) потомств разных плюсовых деревьев, отобранных по фенотипу. Такая оценка получается в результате анализа роста и состояния исследуемых семенных потомств плюсовых деревьев в испытательных культурах.
Методологической основой оценки селекционного эффекта в отборе по фенотипу плюсовых деревьев выступают работы отечественных (Серебровский, 1970; Роне, 1980а, б; Петров, 1984; 1987; 1989; Пирагс, 1985; Ефимов, 1991, 1998, 2000; Котов, 1997; Ткаченко, 2000; Царев, 2001; 2003; 2006; 2013; 2014) и зарубежных (Larsen, 1937, 1947; 1956; Stern, 1953; 1960; 1972a, b; Langner, 1955; 1958) специалистов.
Теоретической предпосылкой организации такого анализа выделенных по фенотипу объектов (плюсовых деревьев) выступает представление о том, что в сходных условиях произрастания потомство родителя с «лучшими» генотипическими (генетическими) характеристиками будет (должно быть) лучше, чем потомство или потомства особи или особей с «худшими» генотипическими характеристиками (Царев и др., 2005, стр. 184). Если установленные в ходе таких сравнительных испытаний преимущества одного родителя над другими будут подтверждены статистически, то их (преимущества) можно считать обусловленными генотипически. На основании таких теоретических представлений строят программы определения генетической ценности объектов, выделенных по фенотипу, в частности плюсовых деревьев. Основным содержанием таких программ выступает ранжирование отобранных фенотипов по их генетическим качествам и ценности (Царев и др., 2005, стр. 184).
Подавляющее большинство видов деревьев и кустарников относятся к перекрестно опыляемым или аллогамным видам. Несмотря на то, что практически все они к тому же не является абсолютными аллогамными видами (строгими перекрестно опылителями), у которых отсутствует самоопыление, они формируют аллогамные популяции в полном смысле этого слова. Особи таких популяций произошли от родительских организмов (отцовского и материнского растений), не идентичных по своим генотипам, и по этой причине сами популяции характеризуются сравнительно высокой степенью гетерозиготности. Проявление признаков таких растений определяется не только собственно генетическим эффектом – действием аддитивных генов или аддитивным эффектом, но и неаддитивными эффектами или эффектами межаллельного взаимодействия (доминирование и сверхдоминирование). Поскольку неаддитивные эффекты связаны с гетерозиготным состоянием, то для сохранения их положительного (в селекционном отношении) влияния, следует обеспечивать сохранение у отобранных объектов высокого уровня гетерозиготности (Гужов др., 1991, стр. 152). В противовес этому проявление аддитивного эффекта не связано с тем, в каком из двух возможных состояний: гетерозиготном или гомозиготном находится генотип рассматриваемого объекта.
Вместе с тем признается (Гужов др., 1991, стр. 152), что продуктивность (в том числе и темпы прироста по запасу древесины или урожайность орехов, смолопродуктивность или количество технического ивового прута, накопление салициловой кислоты в коре ивы или дубильных веществ в коре дуба Б.В.П.) особей аллогамных популяций зависит не от степени гетерозиготности как таковой, а от того, в какой мере гены, привносимые в зиготу от материнского и от отцовского растений (материнской и отцовской гаметами), проявляют положительное аддитивное действие или межаллельное взаимодействие – от проявления аддитивного и неаддитивного эффектов в результате слияния гамет конкретных родительских форм. Тогда мы подошли к представлению о том, что индивидуальная продуктивность особей в аллогамных популяциях определяется комбинационной способностью их родительских форм. Способностью родительских форм образовывать при комбинации своих генотипов в результате слияния их гамет (их взаимного опыления) зиготы, в которых их признаки сочетаются таким наилучшим образом, что обеспечивают наибольшую продуктивность в широком смысле (В.П.) В соответствии с представлениями о двух видах действия генов: аддитивном и неаддитивном, – комбинационная способность состоит из двух компонентов: общей комбинационной способности (ОКС), обусловленной аддитивным действием генов, и специфической комбинационной способности (СКС), определяемой эффектом неаддитивного взаимодействия генов (Гужов и др., 1991, стр. 152).
Общие представления о комбинационной способности и трактовка её основных теоретический положений к настоящему времени сложились в полной мере (Райт, 1978; Рокицкий, 1978; Роне, 1980 б; Биргелис, 1981; 1988; Фолконер, 1985; Айала, 1988 а, б; Гужов, 1991; Царев, 2003; Бессчетнов, 2005 в; 2006; Бессчетнова, 2005 а; 2008 а, б; 2009 а, б, в 2016; Griffing, 1956 a, b; Das, 1998; Bailey, 2006; Han, 2008; Kamunya, 2009; Souza, 2009; Kroon, 2009; 2011; Mahdy, 2011).
Селекция древесных и кустарниковых видов, называемая лесной селекцией, оперирует преимущественно методами отбора, приемлемыми для работы в аллогамных популяциях. Они (эти методы) различаются тем, какая именно форма комбинационной способности преобладает у вида, который подвергают селекционному совершенствованию.
Известны методы отбора, основывающиеся на использовании эффекта общей комбинационной способности. Одним из них является повторяющийся (рекуррентный) отбор на общую комбинационную способность, другим – поликросс-тест. Их применение считается обоснованным, если неаддитивная (обусловленная доминированием) варианса значительно меньше, чем половина аддитивной генетической вариансы. Если же неаддитивная генетическая варианса, обусловленная эффектом доминирования, составляет больше половины аддитивной генетической вариансы, то имеются основания ожидать большего эффекта от отбора на специфическую комбинационную способность. Так поступают при селекции на гетерозис. Кроме того, возможен и одновременный отбор на достижение эффектов общей и специфической комбинационной способности – реципрокный повторяющийся отбор (Гужов и др., 1991, стр. 152).
Признается возможность оценки уровня генетической обусловленности селекционных преимуществ отобранных растений на основании испытания их клонов как первый этап определения генетического качества результатов селекции, например: плюсовых деревьев (Райт, 1978; Гужов, Фукс, Валичек, 1991, стр. 156). Такие сравнительные испытания вегетативных потомств возможны на соответствующих ЛСП и в архивах клонов. Идеология такого сравнительного испытания клонов выделенных по фенотипу плюсовых деревьев соответствует принципам клонового отбора, который в свою очередь базируется на реализации принципов близнецового метода (Айала, 1984, стр. 146 – 147; Айала, Кайгер, Т-2, 1988, стр. 357 - 359). Сравнительные испытания клонов проводят с целью выявления генотипической ценности выделенных по фенотипу плюсовых деревьев; ценны ли «элитные» растения не только фенотипически, но и генотипически. Ответ на это вопрос дают, исходя из постулата о том, что продуктивности клонов, полученных от более продуктивных объектов, также должна быть большей. Если это подтверждается в ходе сравнительных испытаний клонов исследуемых плюсовых деревьев, то приход к выводу о большей генотипичеси обусловленной продуктивности и самих плюсовых деревьев.
Емкое определение понятию «комбинационная способность» дают Г.В. Гуляев и В.В. Мальченко (1975, стр. 71).
Комбинационная способность – это способность линии или сорта при сочетании их в гибридных комбинациях давать потомство (F1), характеризующееся различным относительно некоторого, условно принятого уровня выражением того или иного признака или свойства (Гуляев, Мальченко, 1975, стр. 71).
Они же (Гуляев, Мальченко, 1975, стр. 71) дают расшифровку предложенного определения. При существенном (факт существенности необходимо доказать в ходе дисперсионного анализа Б.В.П.) превышении над данным уровнем выражения исследуемого признака у потомства говорят о высокой комбинационной способности родителей. Определение комбинационной способности линий и сортов, а в лесной селекции плюсовых деревьев, является очень важным этапом в современной селекции на гетерозис у многих растений.
Принципиальная возможность применения методов генетического анализа популяций при работах с объектами ПЛСБ и ЕГСК определена принадлежностью составляющих их плюсовых деревьев к единой популяции. Все они должны быть отобраны в установленном порядке (Вересин, 1963; Временные рекомендации…, 1966; Указания о порядке отбора…, 1972; Основные положения по лесному семеноводству…, 1976; 1991; Указания по лесному семеноводству…, 2000) из состава естественных насаждений региона, что следует из содержания паспортов и описания плюсовых деревьев, введенных в ассортимент ЛСП.
При модернизации существующих представлений о комбинационной способности, выполненной на кафедре лесных культур Нижегородской ГСХА (Бессчетнова, 2016 а, 2016 б) мы исходили из того, что генотип каждого из них представляет собой часть генофонда общей популяции, из которой они были выделены. Сложность процессов взаимодействия генотипа особей и экологического фона, на котором сформировались популяции древесных видов, специфика их биологии, исключающая или существенно ограничивающая возможность применения в испытаниях по-вторяющихся смен поколений, делает нереальной реализацию исчерпывающего генетического анализа, обусловливает необходимость рассматривать упрощенные и формализованные модели популяций (Правдин, 1971; Роне, 1980а, б; Котов, 1997). В такой ситуации важно определить, насколько адекватно характеристики модели отражают свойства популяции. На лесосеменных плантациях при установленных схемах смешения клонов и размещения посадочных мест складываются условия для свободного и, в идеале, полного обмена генетической информацией между растениями, представляющими собой вегетативные потомства разных плюсовых деревьев. Вероятность возникновения самоопыления при этом сведена к минимуму. Пространственная структура ЛСП соответствует представлению о популяции как о системе организмов со случайным распространением генов. В известной мере ЛСП можно принимать как модель популяции (Правдин, 1971; Бороевич, 1984). ЛСП рассматривалась нами как модель популяции исключительно в отношении возможности осуществления на ней свободного опыления составляющих её особей (при оценке ОКС методом поликросс-теста). Кроме этого, мы считали возможным применить такую терминологию на основании того, что популяция традиционно рассматривается как группа особей одного вида, занимающая определенную территорию и имеющую определенные пространственно-репродуктивные взаимоотношения, в рамках реализации которых существует возможность для свободного (в границах популяции) обмена генетическим материалом (Завадский, 1968; Правдин, 1971; Гуляев, 1975; Филипченко, 1978; Айала, 1984; 1988а, б; Бороевич, 1984; Фолконер, 1985; Реймерс, 1990). Мы рассматривали ЛСП как совокупность живых организмов, в той или иной степени соответствующую понятию популяция по ряду своих характеристик:
- наличие в породном составе особей только одного вида (видовая гомогенность и монотипность в репродуктивной сфере);
- единство территории с четко обозначенными границами (пространственно-территориальный критерий общности особей совокупности);
- выраженная в той или иной степени территориальная и репродуктивная обособленность от других популяций и особей того же вида (аспект локальной изоляции от остальных особей того же вида);
- свободный и полный обмен генетической информацией между особями в пределах границ совокупности (способность к панмиксии или аспект потенциально полного генетического взаимообмена);
- нахождение на определенной территории особей в данном составе и соотношении в течение достаточно продолжительного времени, настолько продолжительного, что становится возможным их многократное репродуктивное взаимодействие и формирование семенных генераций, способных обеспечить смену семенных поколений (временной аспект репродуктивного взаимодействия особей, составляющих совокупность).
Кроме того, на ЛСП вегетативного происхождения создаются необходимые предпосылки для полного, равномерного и сбалансированного опыления каждого ортета, представленного некоторым набором своих клонов – рамет, пыльцой всех остальных плюсовых деревьев, введенных в ассортиментный состав. Следовательно, на репродуктивно изолированной от несанк-ционированного заноса пыльцы лесосеменной плантации реализуется неконтролируемое опыление плюсовых деревьев по схеме поликросса. Тогда у нас возникают основания рассматривать отдельную ЛСП как поликроссное поле, выступающее источником семян при проведении генетического анализа семенного потомства полусибсов плюсовых деревьев по системе поли-кросс-теста (Кедров-Зихман, 1974; Райт, 1978; Рокицкий, 1978; Фолконер, 1985; Гужов, 1991; Sprague, 1942; Hinkelmann, 1963; Dey, 1994; Gupta, 1994; Singh, 1995; Mukerjee, 1997; Olfati, 2012; Azad, 2014): все варианты перекрестного опыления при исключении самоопыления.
Сложность организации и высокая трудоемкость контролируемых скрещиваний на объектах постоянной лесосеменной базы выдвигают в число основных критериев оценки селекционных преимуществ и генетической ценности плюсовых деревьев, выделенных по фенотипу, их общую комбинационную способность (Петров, 1981). Вместе с тем, известные алгоритмы вычисления оценок общей комбинационной способности (Райт, 1978; Рокицкий, 1978; Фолконер, 1985; Гужов, 1991; Котов, 1997; Царев, 2003) не определяют конкретный порядок расчета этих величин при реализации поликросс-теста, в частности в варианте свободного опыления на лесосеменных плантациях. Отсутствуют и однозначно трактуемые представления о правилах использования в таких расчетах контроля.
В селекции растений хорошо известно, что не каждое скрещивание двух линий (родительских форм или плюсовых деревьев) приводит к получению гетерозисных гибридов, так как различные генотипы в неодинаковой степени способны обеспечить эффект гетерозиса. Чтобы найти наиболее приспособленные для этого плюсовые деревья, формы, лини или в конечном итоге сорта необходимо проводить диаллельные скрещивания, в которых каждую изучаемую родительскую форму (плюсовое дерево, гибрид, линию) скрещивают с каждой другой изучаемой родительской формой (плюсовым деревом, гибридом, линией). Полученные вследствие этого семенные потомства испытываемых объектов совместно выращивают на специальных участках – испытательных культурах.
Поскольку селекционерам приходится иметь дело с сотнями и даже тысячами линий, сортов и форм (коллекции вегетативных репродукций плюсовых деревьев сосны обыкновенной в Семеновском специализированном семеноводческом лесхозе или лиственницы сибирской в бывшем Волжском лесхозе Нижегородской области превышают сотни единиц), то перекомбинировать их во всех сочетаниях не представляется возможным. Вследствие этого все многообразие исходных родительских форм нередко объединяют в небольшие группы по 8 – 10 форм (наиболее различающиеся в признаках или по происхождению при реализации стратегии скрещивания наиболее отдаленных родительских форм) или линий, и затем проводят диаллельные скрещивания в пределах каждой из них в отдельности.
Схема диаллельного скрещивания, как правило, представляется в виде таблицы («решетки»). Один из её вариантов для 6 родительских форм приведен ниже (табл. 1).
Таблица 1.
Схема полных диаллельных скрещиваний шести родительских форм
с исключением самоопыления
| ♂ ♀ | Родительские формы | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| Родительские формы | 1 | - | 1 х 2 | 1 х 3 | 1 х 4 | 1 х 5 | 1 х 6 |
| 2 | 2 х 1 | - | 2 х 3 | 2 х 4 | 2 х 5 | 2 х 6 | |
| 3 | 3 х 1 | 3 х 2 | - | 3 х 4 | 3 х 5 | 3 х 6 | |
| 4 | 4 х 1 | 4 х 2 | 4 х 3 | - | 4 х 5 | 4 х 6 | |
| 5 | 5 х 1 | 5 х 2 | 5 х 3 | 5 х 4 | - | 5 х 6 | |
| 6 | 6 х 1 | 6 х 2 | 6 х 3 | 6 х 4 | 6 х 5 | - | |
Все комбинации в левой стороне ниже диагонали – это прямые скрещивания, а все комбинации в правой стороне выше диагонали – это обратные скрещивания. Все вместе они составляют полную схему диаллельного реципрокного скрещивания для однодомных видов деревьев и кустарников.
Диаллельные скрещивания – это скрещивания испытуемых деревьев во всех возможных комбинациях.
Полученные в результате скрещиваний гибриды испытывают в полевом опыте в испытательных культурах по хозяйственно важным или адаптивным признакам (быстрота роста, качество ствола и древесины, устойчивость и др.) в соответствии с поставленной целью селекции.
ДОПОЛНЕНИЕ
В ряде случаев для оценки селекционных качеств плюсовых деревьев применяют сравнительную оценку их семенных потомств в процессе сравнительного изучения сеянцев на ранних этапах их развитии. Это мажет иметь значение для оценки способности семенного потомства плюсовых деревьев к высоким темпам роста в ранних фазах оногенеза
Оценка родительских форм на комбинационную способность может быть проведена на основании изучения их гибридов F1 (в полевых и лабораторных испытаниях) по двум критериям:
- общей комбинационной способности (ОКС) и
- специфической комбинационной способности (СКС).
Существует немало определений понятия «комбинационная способность». Нередко они заметно различаются по своему содержанию. Это указывает на достаточную сложность рассматриваемого вопроса, отсутствие единого всеобъемлющего определения и неоднозначное представление о нем.
Одно из наиболее удачных определений звучит так.
Комбинационная способность – это степень выраженности признаков родителей в первом поколении гибридов F1 .
Весьма важное дополнение в это определение сделал Дж. В. Райт (1978).
Комбинационная способность – это относительная способность организма передавать генетическое превосходство своим потомкам (Райт, 1978, стр. 446).
Термин относительная в определениях, предложенных Дж. В. Райтом (1978), совершенно справедливо подчеркивает то, что оценка ОКС или СКС имеет отношение только к данному (учитываемому в данном опыте или в данном конкретном случае, а не вообще) анализируемому комплексу (набору) потомств плюсовых деревьев – только к данному комплексу сравнительно оцениваемых плюсовых деревьев. При этом, как правило, предусматривается, что данный комплекс потомств плюсовых деревьев испытывается в составе одних испытательных культур. Оценка ОКС или СКС имеет значение только относительно тех деревьев, которые были задействованы в каждом конкретном случае учета или анализа. Значения ОКС и СКС одного и того же ПД в разных схемах испытаний с разными наборами других ПД, с которыми оно будет комбинироваться, будут различными, и ранг качества конкретного ПД в разных комплексах сочетаний с другими ПД будет не однозначным.
Не вполне удачное, на мой взгляд (В.П.) определение приведено в учебнике Селекция и репродукция лесных древесных пород (Царев и др., 2003).
Комбинационная способность – это способность одного родителя (линии, клона ПД) в сочетании с другим родителем (линией, клоном ПД) давать потомство, характеризующееся определенным уровнем признака или свойства, или относительная способность организма передавать генетическое превосходство своим потомкам (Царев и др., 2003, стр. 485).
Оно требует существенных разъяснений, несмотря на то, что в целом вполне корректно. То, что изложено в первой части определения свойственно любому организму: любой из «родителей» способен давать потомство в сочетании с «другим родителем», при этом, безусловно, потомство будет обладать определенным уровнем признака или свойства (иначе и не бывает), на которое мы обращаем внимание при селекции. Здесь, очевидно, авторы определения хотели подчеркнуть аспект, который определяет название термина «комбинационная». Да, это способность к комбинации (сочетанию) одного «родителя» с другими «родителями». Однако содержательный момент понятия «комбинационная способность» в этом определении отсутствует. Следовало бы указать на то, что «комбинационная способность» как показатель, служит мерой или относительной оценкой способности «родителя» передавать (в той или иной степени) свои лучшие признаки и свойства потомству: либо вообще в любых комбинациях (ОКС), либо только в конкретных комбинациях (СКС). Вторая же часть этого определения авторами была позаимствована у Дж. В. Райта (1978, стр. 446) без каких либо изменений и ссылок на него.
Различают общую и специфическую комбинационную способность.
2. Испытательные культуры как средство проведения генетического анализа в лесной селекции
.
3. Сравнительные испытания семенных потомств в ранних фазах онтогенеза
4. Общая комбинационная способность
Традиционно принимается следующее определения понятия «общая комбинационная способность».
Общая комбинационная способность – это оценка генетического качества каждого отдельного родителя, установленная в испытаниях потомков-полусибов.
Экстраполируя это определение на лесную селекцию, можно уточнить, что «родителем» будет выступать плюсовое дерево, а в более широком смысле – любой объект селекции: например, любое отобранное дерево (особь), используемое в процессе гибридизации или участвующее в процессе получения мутантов или полиплоидов.
Весьма удачное определение этого понятия предложил Дж. В. Райт (1978).
Общая комбинационная способность – это относительная способность организма передавать свое генетическое превосходство потомкам при скрещивании с любыми другими организмами этого вида. Высокая ОКС обычно указывает на наличие генов с аддитивным эффектом (Райт, 1978, стр. 447).
Термин относительная в определениях, предложенных Дж. В. Райтом (1978), совершенно справедливо подчеркивает то, что оценка ОКС или СКС имеет отношение только к данному (учитываемую в данном опыте или в данном конкретном случае, а не вообще) анализируемому комплексу потомств плюсовых деревьев – только к данному комплексу плюсовых деревьев. Оценка ОКС или СКС имеет значение только относительно тех деревьев, которые были задействованы в каждом конкретном случае учета или анализа.
Свое определение предложили и авторы учебника А.П. Царев и др. (2003).
Общая комбинационная способность – это средняя ценность одного родителя (линии, клона) на основе его поведения в скрещивании с другими родителями (линиями, клонами). Оценка проводится по потомству на основе диаллельных скрещиваний, методов топкросса, поликросса или свободного опыления (Царев и др., 2003, стр. 485).
ОКС представляет собой среднюю оценку отклонения потомков данного генотипа (потомков одного плюсового дерева) от средних значений признака у всех полученных гибридов всех генотипов, включенных в опыт (Царев и др., 2003, стр.117).
По определению Д. С. Фолконера (1985), ОКС представляет собой среднее значение по всем F 1 , для которых данная линия является родительской, и её величина выражается как отклонение от общего среднего по всем кроссам. При реализации поликросс-теста данное определение Д.С. Фолконера (1985) позволяет рассматривать среднюю величину признака каждой полусибсовой семьи как среднее значение по всем F 1 , для которых данная линия является родительской.
Исходя из приведенных тезисов, удается обозначить весьма существенную сторону оценки ОКС (оценки как величины и как процесса или алгоритма). Обязательным условием вычисления значения ОКС какого либо объекта (плюсового дерева) является сравнительное испытание его семенных потомков-полусибсов (или сибсов) в комплексе полусибсовых семей, полученных в такой системе скрещиваний (диаллельные разной модификации, поликросс, топкросс), при реализации которой образуется набор семенных потомств: полусибсовых семей, или сибсовых семей, – характеризующихся родственными отношениями не только внутри семьи (что само по себе разумеется), но и относительно друг друга. Каждая из семей обладает некоторой частью общих и для всех других семей генов, что обеспечено собственно принятыми в испытаниях системах скрещиваний (диаллельные разной модификации, поликросс, топкросс).
Вместе с тем действующими в настоящее время нормативными документами, регламентирующими реализацию селекционных мероприятий в сфере лесного семеноводства на генетико-селекционной основе (Указания …, 2000, п. 4.2, стр. 14), дано свое вполне конкретное определение этого понятия и обозначен порядок получения итоговых значений оценок.
Общая комбинационная способность плюсового дерева определяется как средняя величина превышения показателя исследуемого признака над контролем у его семенного потомства, полученного от скрещивания данного дерева с любыми деревьями того же вида, в том числе при свободном опылении (Указания …, 2000, п.4.2, стр. 14).
Она состоит в способности одних родителей скрещиваться («комбинироваться») с другими и давать в результате этого наилучших потомков. Принято считать, что родитель, дающий в целом наилучшее потомство, обладает большей общей комбинационной способностью (ОКС).
Слово «сиб» (сокращение от слова “sibling”) – общий термин для обозначения брата или сестры. У полу-братьев или полу-сестер («полусибсов») известен один общий родитель (мать или отец), но не оба родителя одновременно. У деревьев-полу-сибсов общий родитель, как правило, семяобразователь или (значительно реже) общий пыльцевой родитель, но не оба родителя.
Оценкой общей комбинационной способности (ОКС) растения служит мера отклонения от «контроля – обобщенного среднего» (Котов, 1997) среднего значения селектируемого признака у совокупности всех гибридов F1 , полученных во всех комбинациях скрещивания, где одним из родителей было испытуемое (анализируемое) дерево (плюсовое дерево).
С помощью ОКС выявляют плюсовые деревья (линии), давшие в среднем наиболее продуктивные гибриды. Для этого по каждой родительской форме (линии, плюсовому дереву) определяют средние показатели селектируемого признака для всех гибридов, в создании которых она участвовала (как отцовская, либо как материнская, либо и в той и другой форме). Родительские формы (линии, ПД), гибриды которых характеризуются высокими средними показателями селектируемого признака, признаются формами с высокой общей комбинационной способностью. Таким образом, показатель ОКС всегда относится к одной конкретной родительской форме – особи (линии, плюсовому дереву – генотипу).
Оценки ОКС отобранных особей (плюсовых деревьев, гибридов и т.п.) используется при выборе лучших деревьев для семенных плантаций; для генетической браковки худших объектов в существующих ЛСП; при выборе родительских пар для генетического улучшения деревьев.
Общую комбинационную способность определяют, как правило, на основе топкроссных испытаний, при осуществлении которых проводят скрещивание изучаемых линий (плюсовых деревьев) с одним общим тестером – своего рода эталоном для сравнения линий, плюсовых деревьев, гибридов (Рокицкий, 1978, стр. 364). Вместе с тем существуют схемы (М.М. Котов, 1997), где рекомендовано поликроссное скрещивание или поликросс, что легко реализовать на лесосеменных плантациях при их удовлетворительной изоляции от других источников пыльцы (от неконтролируемого заноса пыльцы извне).
Топкроссные скрещивания – это скрещивания, при которых все участвующие в испытании растения опыляются пыльцой одного из них. (Котов, 1997, стр. 133).
Топкроссное скрещивание – это скрещивание некоторого числа родительских форм (линий, плюсовых деревьев) с одной определенной формой (линией, плюсовым деревом), которая называется тестером. Если в качестве тестера используется существующий сорт, то его называют сорт-тестер. (Гужов и др., 1991).
От сорта-тестера или формы-тестера требуется, чтобы он обладал по возможности средней ОКС. В этом случае, как правило, лучше различается ОКС линий, чем при использовании тестера с высокой ОКС. Использование тестера с высокой ОКС приведет к нивелированию различий между сравниваемыми родителями.
В качестве тестера можно использовать как отцовское растение (его пыльцой опыляют все остальные растения), так и материнское растение (его цветки или макростробилы опыляют пыльцой со всех остальных растений). В первом случае необходима кастрация всех источников пыльцы, не являющихся тестером, во втором – ручное опыление с использованием изоляторов. Считается, что использование в качестве тестера материнского растения имеет преимущества, заключающиеся в том, что все образовавшиеся семена (при их различной генетической конституции) будут иметь одинаковые (в той или иной степени) посевные качества (размер, запас питательных веществ и пр.), поскольку будут сформированы на одном растении (одна корневая система, одинаковое водообеспечение, корневое питание и т.п.). Кроме того, в этой ситуации исключено влияние на образование различий «материнского эффекта».
Поликросс – это система скрещиваний, в которой на специально созданных участках (питомниках, лесосеменных плантациях) исследуемые деревья свободно опыляются пыльцой других растений, растущих на том же участке (питомнике, лесосеменной плантации) (Котов, 1997, стр.133).
Таким образом, поликросс следует рассматривать как одну из систем скрещиваний – одну из числа применяемых систем простых скрещиваний. Очевидно, следует также учесть то обстоятельство, что результатом осуществления поликроссных скрещиваний будет комплекс полусибсовых семей, каждая из которых представляет генеративное потомство (набор гибридов) отдельного (данного) плюсового дерева со всеми остальными плюсовыми деревьями, участвующими в испытании. Тот же набор полусибсовых семей с принципиально таким же набором гибридов в каждой из них будет получен при реализации реципрокной диалельной схемы скрещиваний.
Здесь следует ввести ограничение понятию свободное опыление – оно предусматривает свободное опыление только в границах испытываемых особей, участвующих в диаллельном анализе, при исключении какой-либо возможности заноса пыльцы извне.
ВНИМАНИЕ!
Здесь, очевидно, предусматривается возможность раздельного анализа поколений F1 от каждого исходного родительского дерева. Кроме того, очевидно, принимается допущение о равноценности условий опыления каждого из анализируемых на ОКС родителей всеми остальными родительскими формами в полном представительстве опыления всех других форм на данной анализируемой форме.
Соответствующие методы определения комбинационной способности разработал Б. Гриффинг (B. Griffing, 1956) (по Рокицкому, 1978; Гужову и др. 1991), предложивший четыре метода анализа диаллельного скрещивания.
1. Изучают родительские формы и реципрокные гибриды F1; число вариантов опыта равно р2 (варианты самоопыления исключены).
2. Изучают родительские формы и гибриды F1 одностороннего диаллельного скрещивания; число вариантов равно 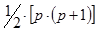 .
.
3. Изучают только реципрокные гибриды F1; число вариантов скрещивания 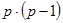 ; варианты самоопыления исключены.
; варианты самоопыления исключены.
4. Изучают только гибриды F1 одностороннего диаллельного скрещивания без родительских форм; число вариантов опыта составляет 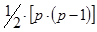 .
.
Для анализа комбинационной способности в целях гетерозисной селекции, как правило, применяют метод 4. Тоже можно сказать и в отношении видов древесных и кустарниковых пород в лесной селекции. Наряду с выбором метода необходимо установить, могут ли существовать между изучаемыми родительскими формами любые родственные отношения (модель 1) или родительские компоненты являются случайной выборкой из определенной популяции (модель 2). Гетерозисная селекция чаще всего основана на предпосылках модели 1.
В лесной селекции часто проводят оценку генетического качества плюсовых деревьев, определяя их ОКС в ходе поликросс-теста, который на ЛСП может быть сравнительно легко реализован в форме свободного переопыления всех рамет всех ПД, введенных в состав ЛСП. Применение такой схемы проведения анализа соответствует 3-му или 4-му методу Гриффинга, когда изучают только потомство, полученное в результате прямых односторонних скрещиваний. С генетической точки зрения такая аналогия вполне приемлема, поскольку в результате реализации свободного опыления на ЛСП будет образовано гибридное потомство каждого отдельного ПД со всеми остальными. Это обусловлено принятыми схемами смешения клонов, многократной повторностью каждого клона, случайным характером размещения на местности их комплекса, поскольку выбор порядкового номера конкретного клона в схеме смешения случаен (на «этом месте» мог оказаться любой из сравниваемых клонов, и не одному из них не было предоставлено каких-либо преимуществ). Тот же комплекс гибридов будет образован в результате поликросс-теста, равно как и в результате прямых односторонних диаллельных скрещиваний, проводимых контролируемо. Действительно, в любом из этих случаев будет получен комплекс кроссов каждого испытываемого ПД с каждым из всех остальных. Именно то обстоятельство, что в результате реализации этих схем возникает один и тот же комплекс потомков, позволяет отнести их к четвертому методу Гриффинга. Тогда возникает предпосылка для проведения анализа в соответствии с этим методом.
Рекуррентный отбор на общую комбинационную способность отличается от повторяющегося (рекуррентного) отбора по фенотипу тем, что не является методом массового отбора.
Рекуррентный отбор по фенотипу относят к одному из методов массового отбора (отбор по фенотипу – основной критерий массового отбора), поскольку на каждом из его этапов идет отбор по фенотипу. Принципиально такой отбор мог бы быть реализован в популяциях древесных видов (перекрестно опыляющихся видов). Однако реальность его применения в этом случае невелика, поскольку повторяющийся отбор рассматривается как отбор по фенотипу, повторяющийся в последующих генеративных поколениях. Отбор по фенотипу плюсового дерева выступает в этом отборе первым этапом. На следующем этапе должен быть предусмотрен отбор по фенотипу лучших из потомков данного плюсового дерева, а на следующем – лучших из потомков лучшего потомка исходного плюсового дерева и т.д. Легко понять, что при работе с деревьями и кустарниками такой отбор потребует (займет) слишком много времени, особенно если оценку потомства проводить в возрасте 50 лет, что рекомендовано при изучении испытательных культур, или если учесть, что возраст вступления в генеративную фазу некоторых древесных видов весьма велик: у сосны кедровой сибирской – 90 лет (в насаждениях).
Рекуррентный отбор на общую комбинационную способность основан на принципах индивидуального отбора. Как правило, такой отбор реализуется через сравнительные испытания потомств отобранных плюсовых деревьев (или гибридов, или мутантов и т.п.), полученных в результате их скрещивания с объектом-тестером (сортом-тестером или плюсовым деревом-тестером). Отбор по фенотипу плюсового дерева (или иного продукта селекции) в этом типе отборе (схеме отбора) выступает первым этапом. На последующих периодах отбора он (отбор) реализуется как отбор лучших особей по результатам испытаний их потомств (а не по фенотипу, как в рекуррентном отборе по фенотипу).
При невозможности или затрудненности проведения скрещиваний с сортом-тестером (по экономическим – очень дорого, или техническим – сложности опыления или изоляции, или иным причинам), для определения ОКС выделенных по фенотипу объектов (плюсовых деревьев, гибридов, мутантов и т.п.) допускается использование свободного опыления между собой растений, образующих анализируемый комплекс. По Гужову и др., 1991, такой комплекс называется «популяцией исходного материала», в смысле материала, отобранного по фенотипу. Именно «популяция исходного материала» подвергается рекуррентному отбору на ОКС. При этом авторы (Гужов и др., 1991, стр. 153 – 155) определяют (обозначают, подчеркивают) то обстоятельство, что на первом этапе такого отбора из некоторой совокупности выделяют «элитные» объекты по фенотипу. В лесной селекции такая работа адекватна выделению плюсовых деревьев. Эти «элитные» объекты формируют «исходную популяцию», которая и подвергается повторяющемуся отбору на ОКС.
Тогда очевидным становится весьма важное обстоятельство организации работ по рекуррентному отбору на ОКС путем свободного опыления:
- необходимость участия в свободном опылении всех особей или объектов «исходной популяции» с одной стороны, и
- участие в таком свободном опылении только особей данной «исходной популяции» с другой стороны.
Это обеспечивает включение в расчетные схемы по определению величин ОКС, данных только по семьям, полученным от такого опыления. Необходимость такого подхода к организации отбора на ОКС обусловлена тем, что в расчетные схемы требуется включение известной заранее доли дисперсии. Такой известной долей дисперсии выступает дисперсия между близкими родственниками – близнецовый метод. Все испытываемые полусибсовые семьи должны обладать некоторой долей генетической общности. Каждая из них имеет структуру генотипа принципиально одинакового (такого) характера. В составе полусибсовой семьи ½ генотипов у всех особей полусибсовой семьи (относится к генотипу) определена генотипом инициальной особи (особи, инициирующей происхождение полусибсовой семьи – общего родителя) и является общей для данной полусибсовой семьи, но и специфичной для каждой полусибсовой семьи. Вторая ½ генотипов – вторые «половинки генотипов» – представляет собой набор или комплекс генотипов всех остальных особей (плюсовых деревьев), участвующих в испытании. При этом комплекс таких «вторых половинок» у всех полусибсовых семей различается только по отсутствию в его составе генотипа данной инициальной особи – варианты самоопыления исключены, а в остальном – одинаков.
Испытание на комбинационную способность по данному методу проводят в полевом опыте по методике испытаний семей. Семенное потомство каждого испытываемо объекта (плюсового дерева), полученное от свободного переопыления, представляет отдельный вариант опыта.
Вместе с тем в классической схеме рекуррентного отбора на ОКС присутствует этап самоопыления части генеративных органов выделенных по фенотипу «лучших» объектов и сочетание этого этапа с одновременным опылением другой части генеративных органов выделенных по фенотипу объектов пыльцой сорта-тестера или, как в лесной селекции, плюсового дерева-тестера. Семена, полученные от скрещивания (опыления) выделенных по фенотипу объектов с сортом-тестером, служат для изучения ОКС плюсовых деревьев («элитных растений» по Гужову и др., 1991, стр. 154.) с применением схемы топкроссных скрещиваний. Их (лучшие объекты) выявляют для того, чтобы использовать семена, полученные от их принудительного самоопыления, для формирования новой «исходной популяции». Её растения (после вступления их в генеративную фазу онтогенеза) могут свободно переопыляться, что должно устранить инцухт-депрессию. Семена, полученные от свободного переопыления особей такой производной «популяции», при их посеве образуют новую популяцию, которая подвергается следующему этапу такого отбора и т.д. Обычно отбор повторяется несколько циклов.
Принципиально такой отбор также мог бы быть реализован в популяциях древесных видов. Однако реальность и его применения и в этом случае крайне мала, поскольку повторяющийся отбор рассматривается как отбор, повторяющийся в последующих генеративных поколениях. Отбор по фенотипу плюсового дерева выступает в этом отборе первым этапом. На следующем этапе должен быть предусмотрен отбор лучших из испытываемых по результатам топкросса семей, что определяет ценность образовавших их плюсовых деревьев. Понятно, что в лесном хозяйстве создание и изучение таких испытательных культур потребует много времени (50 лет и более). Затем установленные лучшие ицухт-линии, точнее инцухт линии лучших по итогам испытания плюсовых деревьев, объединяют в одну общую популяцию – высаживают на площадь общей для них ЛСП специального назначения. Здесь они (а, возможно В.Б., и полученные от них клоны) (после вступления их в генеративную фазу онтогенеза) свободно переопыляются. Полученные в результате этого процесса семена служат для образования следующей популяции – «популяции синтетик». Она выступает «исходной популяцией» для следующего цикла повторяющегося отбора, который будет проведен по первоначальной схеме с самоопылением и скрещиванием с тестером и т.д.
На следующем – лучших из потомков лучших потомков исходной популяции плюсовых деревьев и т.д. Легко понять, что при работе с деревьями и кустарниками такой отбор потребует (займет) слишком много времени, особенно если оценку каждого потомства проводить в возрасте 50 лет, что рекомендовано при изучении испытательных культур.
Полученные таким путем семена служат для формирования
Для преодоления возможной инцухт депрессии полученного материала семенного происхождения в схему рекуррентного отбора вводят этап свободного переопыления потомств (после вступления их в генеративную фазу онтогенеза), показавших наилучший результат по итогам сравнительного испытания. Свободное переопыление устраняет инцухт депрессию.
Поликросс-тест традиционно рассматривается как метод отбора на ОКС (Райт, 1978; Гужов, Фукс, Валичек, 1991, стр. 156; Котов, 1997, стр.133; Царев и др., 2003, стр. 120; Бессчетнова, 2009, 2010), в результате которого удается выделить генотипы, лучшие в анализируемой группе особей – плюсовых деревьев. Применение поликросс-теста наиболее целесообразно в случаях самостерильности рассматриваемых объектов (что в известной мере справедливо для сосны обыкновенной), а также с возникновением сложности в реализации рекуррентного (повторяющегося) отбора на ОКС (что справедливо и типично для большинства древесных видов, и сосны обыкновенной в том числе, поскольку все их особи гетерозиготны в силу аллогамности популяций, а возраст вступления в репродуктивную фазу онтогенеза велик). Исходной посылкой данного метода и его начальным этапом выступает клонирование тестируемых объектов, отобранных по фенотипу из гетерогенного исходного материала в соответствии с задачами селекции – в нашем случае плюсовых деревьев. Созданные в Семеновском специализированном семеноводческом лесхозе клоновые лесосеменные плантации в полной мере отвечают данному условию проведения анализа. Они могут рассматриваться адекватным аналогом поликроссных полей, на которых каждый клон опыляется смесью пыльцы всех остальных клонов, поскольку были заложены по аналогичным требованиям. Важнейшими из них выступают следующие. Каждый клон высаживается в многократной повторности – не менее чем в 10 кратной. Отдельные повторности каждого клона распределяются по площади поликроссных полей – клоновых ЛСП – по принципу рендомизации (что реализовано в схеме смешения клонов по Лангнеру и Штерну, (Рокитский, 1978; Любавская, 1982; Котов, 1997), а также в других схемах смешения клонов на ЛСП), так, чтобы был обеспечен равномерный репродуктивный взаимный контакт каждого из клонов с каждым из других. При этом минимизируются или полностью исключаются варианты самоопыления. Клоны, размещенные на ЛСП – поликроссных полях – должны обладать сходной фенологией, особенно по генеративным фазам: макро- и микроспорогенез плюсовых деревьев хвойных пород должны протекать в одни сроки, – в противном случае не будет обеспечено равномерное участие всех клонов в опылении искусственно созданной клоновой популяции. Если не все клоны полностью самостерильны (что в известном смысле свойственно сосне обыкновенной и другим хвойным видам), то они должны обладать одинаковой самофертильностью (что в пределах вида принимается априори). Схема закладки поликроссных полей должна обеспечивать соответствие блочной схеме полевого опыта, в которой каждый отдельный клон встречается в каждом отдельном блоке учета только один раз, а число блоков соответствует числу повторностей. Это условие в полной мере реализуется блочной схемой смешения на ЛСП (ОСТ 56-74-96, 1996). Поскольку величина ОКС зависит от условий среды, следует проводить опыт в различных экологических условиях. При создании испытательных культур для получения оценки ОКС предусматривается не менее, чем трехкратная повторность (Указания…, 2000).
Дискуссия
В учебниках А.П. Царева и др. (2003, на странице 118) и (2005 на странице 185) говорится (цитирую): «Общая комбинационная способность определяется как среднее значение показателя потомства отдельного дерева, когда оно скрещивается со множеством других деревьев».
Притом, что данное утверждение содержит один весьма важный аспект, характеризующий само понятие ОКС и характеризующий важный этап определения ОКС как оценки, с ним нельзя согласиться в полной мере.
Почему именно так?
Во-первых, ОКС выступает только как относительная оценка генетического качества каждого отдельного родителя (например, плюсового дерева), устанавливаемая в ходе проведения сравнительных испытаний потомств полусибсов или сибсов некоторой группы объектов сравниваемых между собой с цель выявления их ценности относительно друг друга. Тогда существенным моментом такой сравнительной оценки, безусловно, выступает результат сравнения между собой средних величин испытываемых семей (как производных от соответствующих объектов). Точнее говоря, имеет место сравнение объектов (ПД) посредством сравнения характеристик их семей (например, полусибсов) в форме сравнения средних арифметических величин анализируемого признака каждой из семей.
Там же (в тех же источниках) говорится, что ОКС представляет собой среднюю оценку отклонения потомков данного генотипа от средних всех полученных гибридов всех генотипов, включенных в опыт (Царев и др., 2005, стр. 184).
Ранжирование объектов по величине среднего значения анализируемого признака (см. цитату – в ней говорится о средних значениях) позволит выявить наилучшую семью в составе их анализируемого комплекса. Понятно, что «лучшей» данная семья будет только относительно данного комплекса испытываемых семей. Вместе с тем потребуется установление факта существенности различий между «лучшей семьей» и остальными или, что то же самое, доказательство того, что «лучшая семья» действительно «лучше» других, а не является случайным отклонением в пределах ошибки опыта или ошибки распределения. Потребуется доказательство того, что установленный нами факт превосходства одного объекта над всеми другими не является статистически случайным, не лежит в пределах ошибки среднего значения испытываемой совокупности объектов (см. дисперсионный анализ). Потребуется подтверждение того факта, что выявленная «лучшая семья» не относится к единой совокупности, к которой могут принадлежать остальные семьи. Я намекаю на необходимость проведения дисперсионного анализа.
Кроме того, сравнение каждого объекта с каждым из других (по результатам испытания их потомств) позволит выявить, в каких случаях сравнения разница между объектами настолько велика, что может быть признана существенной, а в каких – нет. Это можно установить также только в ходе дисперсионного анализа, используя один из критериев: наименьшую существенную разность (НСР) или D-критерий Тьюки.
Здесь правильно то, что необходимы оценки среднего значения каждого объекта. Однако признать то, что оценка ОКС какого-либо плюсового дерева есть средняя величина признака всех особей его гибридного потомства в испытываемом комплексе, невозможно.
Во-вторых, безусловно, верно то, что оценку ОКС какого-либо дерева можно получить лишь в результате его скрещивания со множеством других. Учитывая же то, что ОКС является относительной оценкой генетического качества отдельного объекта, сравниваемого с другими, но только теми, относительно которых оценка может быть собственно относительной. Иной она быть не может. То есть речь идет о вполне конкретном и однозначно определенном комплексе сравниваемых между собой объектов. Методом сравнения служит сравнительное испытание их потомств (например, полусибсов), полученных в процессе опыления каждого отдельного объекта пыльцой всех остальных (поликросс-тест). Собственно такая организация испытаний и обеспечивает возможность получения относительной оценки не вообще относительной, а относящейся к конкретному комплексу объектов. Однако из сказанного никак не следует, что оценка ОКС какого-либо плюсового дерева – это собственно средняя величина признака всех его гибридных потомков при скрещивании «…со множеством других деревьев».
наилучший объект или группу наилучших объектов
3. Специфическая комбинационная способность.
Специфическая комбинационная способность – это оценка генетического качества каждой из комбинаций родителей в их родительских парах, устанавливаемая по результатам сравнительного изучения потомков-сибсов от разных комбинаций скрещивания.
Она представляет собой оценку способности испытываемых плюсовых деревьев (или иного испытываемого материала) давать в определенных комбинациях скрещивания наилучшее потомство. Та комбинация скрещивания двух родительских форм (двух ПД), которая дает наилучшее по селектируемым признакам потомство, обладает и наивысшей специфической комбинационной способностью.
Специфическая комбинационная способность – это относительная способность организма передавать генетическое превосходство потомкам при скрещивании только с некоторыми другими организмами. Высокая СКС обычно указывает на наличие доминирования, сверхдоминирования и эпистаза (Райт, 1978, стр. 447).
Указаниями по лесному семеноводству в РФ (2000, п. 4.2, стр.14) определен порядок получения оценок ОКС.
Специфическая комбинационная способность плюсового дерева определяется как величина превышения показателя исследуемого признака у его потомства, полученного от конкретной комбинации контролируемого скрещивания с определенным партнером того же или другого вида (Указания …, 2000, п.4.2, стр. 14).
4. Расчет показателей комбинационной способности методами дисперсионного анализа.
Для оценки ОКС и СКС существует целый ряд методов. Наиболее разработанным из них выступает дисперсионный анализ результатов диалельных, а точнее, полиалельных скрещиваний (Рокицкий, 1978, стр. 362). Общеизвестно, что одной из сфер применения дисперсионного двухфакторного анализа является определение общей комбинационной способности (ОКС) и специфической комбинационной способности (СКС) при осуществлении селекции методом отбора (отбор по фенотипу ПД) и методом гибридизации (при оценке наследуемости признаков родителей потомками). В этих ситуациях оценивается степень проявления (сохранения) признаков родителей у потомства первого поколения (F 1). При исследованиях гибридных потомств (селекция методом гибридизации) иерархические комплексы строятся по следующей схеме: иерархическим уровнем высшего порядка (фактор А) выступает один из родительских компонентов (например, отцовские особи), рангом низшего порядка (фактор В) является второй родительский компонент (например, материнские особи); повторностями опыта выступают наборы повторностей каждой комбинации скрещивания (в идеальном случае на нескольких клонах материнской особи при одном источнике пыльцы) в пределах одной комбинации скрещивания.
При оценке ОКС и СКС в ходе испытаний семенных потомств плюсовых деревьев, отобранных по фенотипу, строят не иерархические двухфакторные комплексы. Одним из факторов (фактор А) выступает набор комбинаций скрещивания (диалельных прямых и реципрокных), вторым фактором (фактор В) является набор повторностей каждой комбинации скрещивания (в идеальном случае на нескольких клонах материнской особи при одном источнике пыльцы) в пределах одной комбинации скрещивания.
МЕТОД АНАЛИЗА
Гибриды F 1 изучают в полевом опыте с повторностями в блоках или решетках (латиссы) испытательных культур. В каждом блоке (делянке) необходимо иметь 10 – 15 растений. Изучаемым признаком может быть любой количественный признак, на который ведется селекция в соответствии с её задачами (высота дерева, диаметр ствола, объем или масса стволовой древесины и т.д.). Результаты полевого опыта подвергают дисперсионному анализу, чтобы определить остаточную вариансу 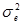 (MSz). Дисперсионный анализ ведут на основе измерения гибридного потомства по каждой родительской форме (для оценки ОКС) и по каждой комбинации скрещивания (для оценки СКС).
(MSz). Дисперсионный анализ ведут на основе измерения гибридного потомства по каждой родительской форме (для оценки ОКС) и по каждой комбинации скрещивания (для оценки СКС).
***************
Внимание!
Выделенное нуждается в обосновании и теоретической доработке.
Примечание:
В учебнике М.М. Котова (стр. 134-135) приведена некорректная схема двухфакторного комплекса: не указывается, что именно является повторностями испытания гибридного потомства (n или r). В рассматриваемом примере по М.М. Котову (1997), Обоснованность введения повторностей в испытательных культурах может быть обоснована следующими положениями.
1. Поскольку в испытательных культурах (по данной схеме) испытываются семенные потомства, то каждая из испытываепмых особей обладает специфическим (неповторяющимся, свойственным только ей) генотипом. Тогда при создании из этих особей испытательных культур распределение генотипов каждой полусибсовой семьи по повторностям будет случайным, но не идентичным – в каждую повторность попадает неповторяющийся набор генотипов (набор генотипов в каждой из повторностей не повторяющийся «каламбур»). Тогда каждая из повторностей опыта может быть представлена как собственно повторность с разным «режимом» «напряженности фактора (фактор – набор генотипов)». Методически введение трёх и более повторностей должно обеспечивать нивелирование действия этого фактора на процесс возникновения и формирования различий между представителями одной полусибсовой семьи или одной семьи полных сибсов.
2. Наборы представителей полусибсовых семей в повторностях размещаются на неповторяющемя в каждой повторности экофоне: каждая повторность испытательных культур территориально размещена на экофоне, который в той или иной степени отличается от экофона других повторностей (или может отличаться), при том, что методически следует предусмотреть выровненность экофона в пределах каждой повторности. Именно это обстоятельство и приводит к необходимости введения в опыт с испытательными культурами повторностей, которые позволяю в итоге добиться статистической однородности экофона под каждой из полусибсовых (или сибсовых семей) и нивелировать различия, вызванные действием внешних факторов или даже (теоретически) исключить, а точнее игнорировать, действие различий в экофоне.
3. При таком методическом подходе к построению опыта, а рассматривается двухфакторный дисперсионный анализ при независимости факторов, статистически каждая из повторногстей какого либо из вариантов скрещивания формируется под действием фактора, обусловленного (представленного) различиями в экологическом фоне и спецификой генетического комлекса семей сибсов или полусибсов.
Вместе с тем, известно (Лакин,1989; Меркурьева, 19** и др.), что результаты дисперсионного анализа (особенно многофакторного) в значительной степени зависят от характера конкретного распределения (конкретной комбинации) действующих факторов по их градациям. В случае, если повторности испытания искусственно выделены в пределах какой либо комбинации скрещивания - скрещивание проведено в пределах одной пары деревьев – они (повторности) по своей сути будут представлять одну и ту же совокупность и будут являться одной и той же выборкой. В такой ситуации распределение всего количества гибридов данной комбинации на повторности испытания гибридного потомства будет абсолютно искусственным и не значимым, что в свою очередь может исказить результаты дисперсионного анализа.
ВНИМАНИЕ!
Здесь (по М.М. Котову, 1997) уместнее (НЕТ!)в качестве высшего уровня иерархии (фактор А) рассматривать отцовские особи (особи, выступающие отцовскими) в комбинациях скрещивания (когда растения выступают источником пыльцы), а в соподчиненном уровне иерархии факторов (фактор В) рассматривать комбинации скрещивания каждого отцовского дерева с различными материнскими (выступающими в качестве материнских) особями. То есть комбинации скрещивания каждого отцовского дерева будут являться градациями фактора низшей иерархии в пределах каждого отцовского дерева, выступающего фактором высшей иерархии.
Вместе с тем в данной схеме можно рассматривать повторности как независимо действующий фактор, определяемый различиями в условиях среды участков под каждой из повторностей.
Вспомним, что диаллельное скрещивание – это скрещивание испытываемых деревьев (и кустарников) во всех возможных комбинациях. Оно может быть прямым (только односторонним прямым), обратным (обратным – по отношению к прямому) и реципрокным (прямым и обратным).
При одностороннем прямом скрещивании без вариантов (случаев) самоопыления число возможных комбинаций скрещивания равно:
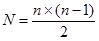 . где
. где
n – число растений участвующих в гибридизации, при условии, что все они однодомны.
При реципрокном (прямом и обратном) скрещивании число возможных комбинаций равно:
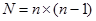 .
.
ПРИМЕР 1. (Реконструкция по Ю.Л. Гужову и др., 1991).
Пусть требуется определить комбинационную способность (вначале ОКС, а затем и СКС) 6 исходных родительских форм ели Тяньшанской (р = 6), при диаллельном прямом скрещивании которых (схема 4) было получено 15 гибридов (а = 15), которые были размещены в 6 повторностях (в = 6) по 12 растений в каждой (с = 12) на опытном участке. Измеряемым параметром выступала высота ствола в 20-летнем возрасте, выраженная в сантиметрах.
Предлагается следующая схема двухфакторного неиерархического дисперсионного анализа (табл. 2).
Таблица 2.
Схема дисперсионного анализа высоты гибридов ели
| № | Источники варьирования | Число степеней свободы, | Средний квадрат, М = ms | Сумма квадра-тов SS | Средний квадрат MS |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1. | Общая дисперсия | a×b×c – 1 = 15×6×12 – 1 = 1079 | My= msy | 20581,6 | |
| 2. | Гибриды | a – 1 = 15 – 1 = 14 | Mg= msg | 11784,6 | |
| 3. | Повторности | b – 1 = 6 – 1 = 5 | Mb= msb | 1680,7 | |
| 4. | Взаимодействие (гиб-риды × повторности) | (a – 1)×(b – 1) = 70 | Mbv= msab | 1334,3 | |
| 5. | Остаток (ошибки) | m = a×b×(c – 1) = 990 | Me= msе | 5782,0 | 5,84 |
ПРИМЕЧАНИЕ.
- В колонке «5» таблицы 2 приведены суммы квадратов отклонений по каждому источнику варьирования без приведения исходных данных по результатам обмеров исследуемых гибридов: таблица исходных данных опускается.
- Средние квадраты отклонений могут быть легко рассчитаны путем деления значения суммы квадратов отклонений по каждому источнику варьирования (колонка 5) на соответствующее ему число степеней свободы (колонка 3).
Из полученного значения для остаточной вариансы Me (5,84) можно вычислить значение Me', необходимое для дальнейшего анализа:
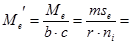
Для нашего примера с 6 повторностями и 12 растениями в каждой повторности это значение будет равно:
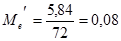
По сути дела полученная таким образом исправленная оценка среднего квадрата отклонений остаточной дисперсии представляет собой отношение суммы квадратов отклонений остаточной дисперсии к исправленному числу степеней свободы
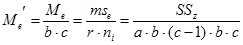
ВНИМАНИЕ!
Схема расчета остаточной дисперсии в учебнике М.М. Котова изложена иначе.
(a-1)*(c-1)*c = (a*c-c-a+1)*c = по схеме М.М. Котова? Корректность формулы вызывает вопрос... Число степеней свободы остаточной дисперсии равно разности между числом степеней общей дисперсии и числами степеней свободы всех организованных факторов: числом степеней свободы дисперсии, вызванной различиями между гибридами (между каждой комбинацией скрещиваний); числом степеней свободы дисперсии, вызванной различиями между повторностями одного гибрида (повторностями одной гибридной комбинации, размещенными на предположительно разном экофоне); числом степеней свободы дисперсии, вызванной взаимодействием факторов «гибриды» и «повторности». Однако в той схеме, которая приводится в учебнике М.М. Котова (1997), в расчете числа степеней свободы остаточной дисперсии не учтена численность собственно вариант (наблюдений, дат, единиц комплекса и т.п.) комплекса.
a×b×(c – 1)×b×c = (a×b×c – a×b) × b×c =
(a – 1) × (r – 1) × n = (a×r – r – a +1) × n = a×r×n – r×n – a×n + n = a×r×n – (r×n + a×n) + n = a×r×n – n×(r + a) + n = a×r×n – n×(r + a) – 1)
ОЦЕНКА КОМПОНЕНТОВ ВАРИАНСЫ
Собственно анализ комбинационной способности проводят по формулам, приведенным в таблице 3 и ниже.
Таблица 3.
Схема дисперсионного анализа для определения комбинационной способности при одностороннем диаллельном скрещивании
ели Шренка (ели тяньшанской)
| № | Источники варьирования | Степени свободы | Сумма квадратов, S | Средний квадрат, М | Теоретически ожидаемое для среднего квадрата по модели 1 |
| 1. | ОКС Разница между семьями полусибсов | 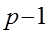
| Sg | Mg | 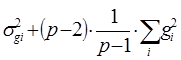
|
| 2. | СКС Разница между семьями сибсов | 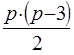
| Ss | Ms | 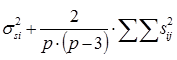
|
| 3. | Остаток (ошибка) | 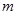 =
a×b×(c–1) =
a×b×(c–1)
| Se | Me | 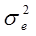
|
Вычисление компонентов проводят по следующим формулам:
Сумма квадратов, обусловленная общей комбинационной способностью (ОКС):
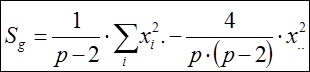
Сума квадратов, обусловленная специфической комбинационной способностью (СКС):
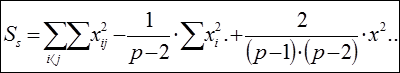
Достоверность эффектов общей и специфической комбинационной способности определяют с помощью F-критерия Фишера.
Для эффектов общей комбинационной способности:
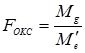
В соответствии с таблицей 3, число степеней свободы равно:
- для значения Mg kg= p – 1;
- для значения Me’ ke= m
Для эффектов специфической комбинационной способности:
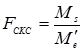
В соответствии с таблицей 3, число степеней свободы равно:
- для значений Ms ks= p(p – 3)/2
- для значения Me’ ke= m
Общую комбинационную способность любой родительской формы (i) определяют по формуле:
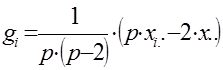
Варианса ОКС определенной родительской формы равна:
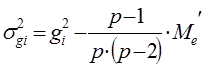
Специфическая комбинационная способность пары родительских компонентов (ij) определяют по формуле:
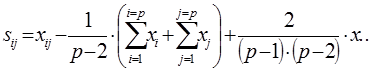
Варианса специфической комбинационной способности определенной родительской формы составляет:
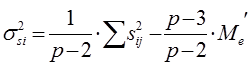
ВЫЧИСЛЕНИЯ
В рассматриваемом нами примере проводилось одностороннее прямое диаллельное скрещивание 6 родительских форм, в результате которого было получено 15 полусибсовых семей гибридного потомства F1. Количество гибридных семей (15) соответствует расчетному числу Гриффинга (1/2 × р × (р – 1)) по варианту «4». Варианты самоопыления исключались из схемы опыта. Характеристики родителей (плюсовых деревьев) также не учитывались. Испытание проводилось в шести повторностях (на 6 разных учетных участках испытательных культур или питомника) по 12 гибридных растений в каждой повторности. Анализировалась высота сеянцев в возрасте 20 лет. Средние значения анализируемого признака, представляющие собой средние арифметические значения по каждой полусибсовой семье из 6 повторностей с 12 гибридными сеянцами в каждой сведены в таблице 4.
Таблица 4.
Средняя для полусибсовой семьи высота ствола (см)
у гибридов F 1 ели Шренка
и исходные значения для определения комбинационной способности
| ♀ | ♂ | |||||||
| Р-1 | Р-2 | Р-3 | Р-4 | Р-5 | Р-6 | x i =Σxij | x i 2 | |
| Р-1 | 81,1 | 83,1 | 82,2 | 81,1 | 82,0 | 409,5 | 167690,25 | |
| Р-2 | 81,1 | 85,1 | 85,0 | 82,0 | 85,0 | 418,2 | 174891,24 | |
| Р-3 | 83,1 | 85,1 | 85,9 | 85,2 | 88,0 | 427,3 | 182585,29 | |
| Р-4 | 82,2 | 85,0 | 85,9 | 87,4 | 88,2 | 428,7 | 183783,69 | |
| Р-5 | 81,1 | 82,0 | 85,2 | 87,4 | 93,0 | 428,7 | 183783,69 | |
| Р-6 | 82,0 | 85,0 | 88,0 | 88,2 | 93,0 | 436,2 | 190270,44 | |
| Σ | 2548,6 | 1083004,60 | ||||||
Помимо экспериментально полученных данных, средних значений высоты ствола для каждой из 6 родительских форм (x ij .), приведенных в верхней правой части матрицы, (для каждого из 6 плюсовых деревьев) вычисляют сумму значений признака (в данном примере по средним значениям для каждой комбинации скрещиваний) у F 1 (F1ij = Рi × Рj) соответствующей полусибсовой семьи: всех потомков-полусибсов каждого одного из испытываемых плюсовых деревьев (Рi) в его сочетаниях со всеми другими (Рj) – (x i = Σ x ij):
| х1 = 81,1+83,1+82,2+81,1+82,0 = 409,5 |
| х2 = 81,1+85,1+85,0+82,0+85,0 = 418,2 |
| х3 = 83,1+85,1+85,9+85,2+88,0 = 427,3 |
| х4 = 82,2+85,0+85,9+87,4+88,2 = 428,7 |
| х5 = 81,1+82,0+85,2+87,4+93,0 = 428,7 |
| х6 = 82,0+85,0+88,0+88,2+93,0 = 436,2 |
и соответствующие квадраты этих сумм (x i 2 = [Σ x ij ]2):
| х12 = (81,1+83,1+82,2+81,1+82,0)2 = 409,52 = 167690,25 |
| х22 = (81,1+85,1+85,0+82,0+85,0)2 = 418,22 = 174891,24 |
| х32 = (83,1+85,1+85,9+85,2+88,0)2 = 427,32 = 182585,29 |
| х42 = (82,2+85,0+85,9+87,4+88,2)2 = 428,72 = 183783,69 |
| х52 = (81,1+82,0+85,2+87,4+93,0)2 = 428,72 = 183783,69 |
| х62 = (82,0+85,0+88,0+88,2+93,0)2 = 436,22 = 190270,44 |
а также общую сумму этих квадратов сумм значений полусибсовых семей по каждому полному набору комбинаций скрещиваний каждого ПД (Σ x i 2); Σ x i 2 = Σ (Σ x ij )2 = 1083004,60 (см. табл. 4, итоговая строка).
На следующем этапе рассчитывают:
- сумму всех значений признака полученных в данной схеме испытаний полусибсовых семей (в рассматриваемом примере только прямые односторонние скрещивания): вычисляется как сумма полученных в данном испытании средних (x ij .) по комбинациям (только прямые скрещивания, см. табл. 4) значений признака (x .. = [Σ Σ x ij .]):
| x .. = 81,1+83,1+82,2+81,1+82,0 + |
| + 85,1+85,0+82,0+85,0 + |
| + 85,9+85,2+88,0 + |
| + 87,4+88,2 + |
| + 93,0 = |
| = 1274,3 |
- квадрат этой суммы (x ..2 = [Σ Σ x ij .]2), x ..2 = (1274,3)2 = 1623840,49;
- общую сумму квадратов значений признака всех гибридов F 1 (F1ij = Рi × Рj) – в нашем случае одностороннего скрещивания (только прямые скрещивания, без вариантов самоопыления), (Σ Σ x 2 ij .), Σ Σ x 2 ij . = 108405,73.
| Σ Σ x 2 ij . = 81,12+83,12+82,22+81,12+82,02 + … |
| + 85,12+85,02+82,02+85,02 + … |
| + 95,92+85,22+88,02 + … |
| + 87,42+88,22 + … |
| + 93,02 = |
| = 108405,73 |
Кроме того, вычисляют полную сумму сумм значений признака (в данном примере по приведенным средним значениям для каждой комбинации скрещиваний) у F 1 (F1ij = Рi × Рj) соответствующей полной полусибсовой семьи: всех потомков-полусибсов каждого одного из испытываемых плюсовых деревьев (Рi) в его сочетаниях со всеми другими (Рj) – (Σxi = Σ Σ x ij , если x i = Σ x ij); показатель используется в расчетах оценок ОКС:
| Σ Σ x ij = 81,1+83,1+82,2+81,1+82,0 + Σ x i = 409,5 + |
| + 81,1+85,1+85,0+82,0+85,0 + + 418,2 + |
| + 83,1+85,1+85,9+85,2+88,0 + + 427,3 + |
| + 82,2+85,0+85,9+87,4+88,2 + или + 428,7 + |
| + 81,1+82,0+85,2+87,4+93,0 + + 428,7 + |
| + 82,0+85,0+88,0+88,2+93,0 = + 436,2 = |
| = 2548,6 = 2548,6 |
полученная величина в формулах дальнейших расчетов ОКС обозначена как «2 × х..». Она соответствует общей сумме всех значений признака полусибсовых групп для полной реципрокной схемы диаллельных скрещиваний получим (Σxi = Σ Σ x ij) Σxi = 2548,6 (см. табл. 4 итоговая строка).
Вычисление компонентов дисперсии проводят по следующим формулам, используя полученные на предыдущем этапе значения.
1. Сумма квадратов, обусловленная общей комбинационной способностью (ОКС) - Sg:
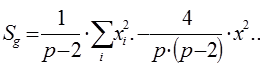 =
=
= 1/(6 – 2) × 1083004,6 – 4/6 × (6 – 2) × 162384,49 = 270751,15 – 270640,08 = 111,07.
2. Сума квадратов, обусловленная специфической комбинационной способностью (СКС) - Ss:
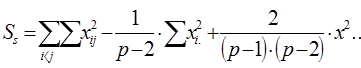 =
=
= 108405,73 – 1/(6 – 2) × 1083004,6 + 2/[(6 – 1) × (6 – 2)] ×1623840,49 = 108405,73 – 270751,15 + + 162384,05 = 38,63.
На следующем этапе составляют таблицу варианс (табл. 5).
Таблица 5.
Таблица варианс для определения комбинационной способности
| Источники варьирования | Степень свободы, k | Сумма квадратов, S | Средний квадрат М |
| ОКС | kg = 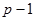 = 6 – 1 = 5 = 6 – 1 = 5
| Sg = 111,07 | Мg = Sg /kg = 22,21 |
| СКС | ks= 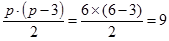
| Ss = 38,63 | Мs = Ss /ks = 4,29 |
| Остаток | ke =a×b×(c–1)×b×c = 71280 | Sе = 5782,00 | М'е=Sе/kе= 0,08 |
Достоверность эффектов общей и специфической комбинационной способности определяют с помощью F-критерия Фишера.
Для эффектов общей комбинационной способности:
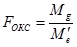 = 22,21 / 0,08 = 277,6 (табличное значение 4,37).
= 22,21 / 0,08 = 277,6 (табличное значение 4,37).
В соответствии с таблицей 3, число степеней свободы равно:
- для значения Mg kg = p – 1 = 5;
- для значения Me’ ke = m = 990.
Для эффектов специфической комбинационной способности:
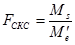 = 4,29 / 0,08 = 53,6 (табличное значение 2,71).
= 4,29 / 0,08 = 53,6 (табличное значение 2,71).
В соответствии с таблицей 3, число степеней свободы равно:
- для значения Ms ks = p(p – 3)/2 = 9;
- для значения Me’ ke = m = 990
Из представленных расчетов и сравнений видно, что и фактическое (опытное, эмпирическое) значение дисперсионного отношения (критерия Фишера) общей комбинационной способности и фактическое (опытное, эмпирическое) значение дисперсионного отношения (критерия Фишера) специфической комбинационной способности превышают соответствующие табличные значения. Это свидетельствует о том, что значения общей и специфической комбинационной способности достоверны. Полученный результат обусловливает возможность и целесообразность (создает основания, предпосылки для) продолжения генетического анализа, который будет состоять в определении общей комбинационной способности для каждой родительской формы (плюсового дерева) и специфической комбинационной способности для каждой их пары в прямых односторонних скрещиваниях.
При диаллельном скрещивании для каждого родительского компонента (i) – любой родительской формы – общую комбинационную способность (gi) определяют по формуле:
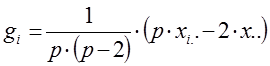
Варианса ОКС определенной родительской формы равна:
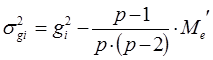
Тогда для каждой из родительских форм (плюсового дерева) получим следующие значения общей комбинационной способности (gi).
g1 = 1/[6×(6 – 2)] × (6 × 409,5 – 2 × 1274,3) = – 3,82
g2 = 1/[6×(6 – 2)] × (6 × 418,2 – 2 × 1274,3) = – 1,64
g3 = 1/[6×(6 – 2)] × (6 × 427,3 – 2 × 1274,3) = 0,63
g4 = 1/[6×(6 – 2)] × (6 × 428,7 – 2 × 1274,3) = 0,98
g5 = 1/[6×(6 – 2)] × (6 × 428,7 – 2 × 1274,3) = 0,98
g6 = 1/[6×(6 – 2)] × (6 × 439,2 – 2 × 1274,3) = 2,86
Оценки вариансы для ОКС каждой особи получают в результате следующих расчетов.
σ2gi = – 3,822 – (6 – 1)/[6×(6 – 2)] × 0,08 = 14,58
σ2gi = – 1,642 – (6 – 1)/[6×(6 – 2)] × 0,08 = 2,67
σ2gi = 0,632 – (6 – 1)/[6×(6 – 2)] × 0,08 = 0,38
σ2gi = 0,982 – (6 – 1)/[6×(6 – 2)] × 0,08 = 0,94
σ2gi = 0,982 – (6 – 1)/[6×(6 – 2)] × 0,08 = 0,94
σ2gi = 2,862 – (6 – 1)/[6×(6 – 2)] × 0,08 = 8,16
Расчеты для каждой родительской формы сводят в таблицу 6.
Таблица 6.
Общая комбинационная способность родительских форм
(плюсовых деревьев) ели Шренка
| Родительский компонент | gi | σ2gi |
| Р1 | - 3,82 | 14,58 |
| Р2 | - 1,64 | 2,67 |
| Р3 | 0,63 | 0,38 |
| Р4 | 0,98 | 0,94 |
| Р5 | 0,98 | 0,94 |
| Р6 | 2,86 | 8,16 |
Специфическая комбинационная способность пары родительских компонентов (ij) определяют по формуле:
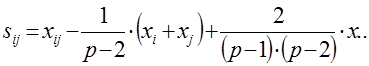
Где:
xi-j – среднее значение признака всех потомков-сибсов каждой конкретной комбинации скрещивания двух родителей (Pi × Pj), участвующих в испытаниях потомств.
xi – сумма значений признака F1 соответствующей полусибсовой группы (всех потомков-полусибсов одного из родителей, во всех его комбинациях с каждым их других плюсовых деревьев) – «первого» из двух родителей (Pi) со всеми остальными.
xj – сумма значений признака F1 соответствующей полусибсовой группы (всех потомков-полусибсов одного из родителей, во всех его комбинациях с каждым их других плюсовых деревьев) – «второго» из двух родителей (Pj) со всеми остальными.
x.. – общая сумма значений признака всех полусибсовых групп (всех полученных в опыте потомков-полусибсов) реализованной в данной опыте (схеме) испытаний потомств прямой схемы диаллельных скрещиваний.
Варианса специфической комбинационной способности определенной родительской формы составляет:
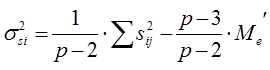
Для всех комбинаций прямого одностороннего скрещивания плюсовых деревьев, участвующих в испытаниях потомств, (родителей) «первого» и «второго» (Р1 × Р2) получим:
S1-2 =x1-2 –1/(6–2)×(x1+x2)+2/(6–1)×(6–2)×x..=81,1–¼×(409,5+418,2)+2/20×(1274,3)=1,60
S1-3 =x1-3 –1/(6–2)×(x1+x3)+2/(6–1)×(6–2)×x..=83,1–¼×(409,5+427,3)+2/20×(1274,3)=1,33
S1-4 =x1-4 –1/(6–2)×(x1+x4)+2/(6–1)×(6–2)×x..=82,2–¼×(409,5+428,7)+2/20×(1274,3)=0,08
S1-5 =x1-5 –1/(6–2)×(x1+x5)+2/(6–1)×(6–2)×x..=81,1–¼×(409,5+428,7)+2/20×(1274,3)=-1,02
S1-6 =x1-6 –1/(6–2)×(x1+x6)+2/(6–1)×(6–2)×x..=82,0–¼×(409,5+436,2)+2/20×(1274,3)=-2,00
S2-3 =x2-3 –1/(6–2)×(x2+x3)+2/(6–1)×(6–2)×x..=85,1–¼×(418,2+427,3)+2/20×(1274,3)=1,16
S2-4 =x2-4 –1/(6–2)×(x2+x4)+2/(6–1)×(6–2)×x..=85,0–¼×(418,2+428,7)+2/20×(1274,3)=0,70
S2-5 =x2-5 –1/(6–2)×(x2+x5)+2/(6–1)×(6–2)×x..=82,0–¼×(418,2+428,7)+2/20×(1274,3)=-2,30
S2-6 =x2-6 –1/(6–2)×(x2+x6)+2/(6–1)×(6–2)×x..=85,0–¼×(418,2+436,2)+2/20×(1274,3)=-1,17
S3-4 =x3-4 –1/(6–2)×(x3+x4)+2/(6–1)×(6–2)×x..=85,9–¼×(427,3+428,7)+2/20×(1274,3)=-0,67
S3-5 =x3-5 –1/(6–2)×(x3+x5)+2/(6–1)×(6–2)×x..=85,2–¼×(427,3+428,7)+2/20×(1274,3)=-1,37
S3-6 =x3-6 –1/(6–2)×(x3+x6)+2/(6–1)×(6–2)×x..=88,0–¼×(427,3+436,2)+2/20×(1274,3)=-0,44
S4-5 =x4-5 –1/(6–2)×(x4+x5)+2/(6–1)×(6–2)×x..=87,4–¼×(428,7+428,7)+2/20×(1274,3)=0,48
S4-6 =x4-6 –1/(6–2)×(x4+x6)+2/(6–1)×(6–2)×x..=88,2–¼×(428,7+436,2)+2/20×(1274,3)=-0,60
S5-6 =x5-6 –1/(6–2)×(x5+x6)+2/(6–1)×(6–2)×x..=93,0–¼×(428,7+436,2)+2/20×(1274,3)=4,20
ПРИМЕР 2. (реконструкция по М.М. Котову, 1997 с необходимой коррекцией и дополнениями В.П. Бессчетнова).
Пусть требуется оценить общую и специфическую комбинационную способность родительских деревьев дуба черешчатого по высоте 20-летнего потомства, полученного от односторонних прямых диаллельных скрещиваний. Исходные данные приведены в таблице (табл. 7).
Расчет ведется по схеме равномерного (ортогонального) дисперсионного двухфакторного комплекса при независимых факторах.
Таблица 7.
Высота гибридов дуба (в возрасте 20 лет)
| № варианта | Комбинация скрещивания | Повторности | Учетные растения | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
| 1 | 1 × 2 | 1 | 5,5 | 5,4 | 6,0 | 6,2 | 6,1 | 6,4 | 6,1 | 6,0 | 5,9 | 6,0 |
| 2 | 5,9 | 6,1 | 6,1 | 6,3 | 5,8 | 5,7 | 5,1 | 6,4 | 6,0 | 6,1 | ||
| 3 | 6,4 | 6,0 | 6,2 | 5,8 | 5,9 | 5,7 | 5,0 | 6,0 | 6,2 | 6,3 | ||
| 2 | 1 × 3 | 1 | 6,5 | 6,5 | 6,1 | 5,5 | 5,4 | 4,9 | 6,1 | 6,3 | 6,4 | 6,3 |
| 2 | 6,0 | 5,9 | 5,8 | 6,3 | 6,5 | 5,2 | 6,3 | 6,2 | 6,1 | 6,1 | ||
| 3 | 6,3 | 6,1 | 5,4 | 5,0 | 6,5 | 6,3 | 6,0 | 5,9 | 5,8 | 5,6 | ||
| 3 | 1 × 4 | 1 | 3,0 | 3,4 | 2,8 | 3,2 | 3,0 | 3,0 | 2,9 | 2,8 | 3,6 | 3,4 |
| 2 | 3,5 | 3,4 | 3,4 | 3,2 | 2,8 | 2,8 | 2,0 | 4,1 | 4,1 | 2,1 | ||
| 3 | 4,0 | 4,1 | 3,2 | 3,1 | 2,5 | 2,5 | 3,8 | 2,1 | 3,0 | 3,1 | ||
| 4 | 2 × 3 | 1 | 3,1 | 3,0 | 2,8 | 2,6 | 3,4 | 3,0 | 2,5 | 2,1 | 2,9 | 3,1 |
| 2 | 4,1 | 3,0 | 3,6 | 3,4 | 2,8 | 2,8 | 2,9 | 3,1 | 3,2 | 3,4 | ||
| 3 | 3,9 | 3,9 | 3,6 | 3,5 | 3,5 | 2,5 | 3,4 | 3,8 | 4,0 | 4,0 | ||
| 5 | 2 × 4 | 1 | 2,5 | 4,1 | 4,1 | 3,9 | 3,5 | 3,5 | 3,9 | 4,0 | 4,9 | 2,6 |
| 2 | 4,1 | 2,6 | 4,1 | 3,9 | 3,6 | 3,8 | 3,8 | 4,1 | 3,6 | 3,8 | ||
| 3 | 4,0 | 4,1 | 4,1 | 4,0 | 4,9 | 3,9 | 3,9 | 3,8 | 3,5 | 3,5 | ||
| 6 | 3 × 4 | 1 | 3,5 | 3,5 | 3,8 | 3,5 | 2,8 | 4,1 | 4,1 | 4,0 | 2,9 | 3,9 |
| 2 | 4,1 | 4,0 | 4,0 | 4,1 | 4,0 | 3,9 | 3,9 | 3,2 | 3,1 | 2,9 | ||
| 3 | 2,8 | 2,9 | 4,9 | 4,1 | 4,0 | 3,8 | 3,8 | 3,8 | 3,4 | 3,0 | ||
Примечание.
Принципиально возможно добавить информацию о дисперсионном анализе – базовая модель, многофакторная модель, иерархическая модель.
Для дальнейших расчетов полезно сформировать таблицу значений степеней свободы для каждого источника изменчивости и численностей градаций каждого из организованных факторов (табл. 8).
Таблица 8.
Числа степеней свободы для разных источников варьирования
| Источник варьирования | Алгоритм вычисления числа степеней свободы | Вычисление числа степеней свободы | Число |
| общая | ky = a × r × n – 1 | ky = 6×3×10 – 1 = | = 179 |
| гибриды | ka = a – 1 | ka = 6 – 1 = | = 5 |
| повторности | kr = r – 1 | kr = 3 – 1 = | = 2 |
| Взаимодействие гибридов и повторностей | kar = (a – 1) × (r – 1) | kar = (6 – 1)×(3 – 1) = | = 10 |
| Остаток или ошибки, или случайная дисперсия: неисправленная величина (m=kz) | kz = ky – ka – kr – kar = (a × r × n – 1) – (a – 1) – (r – 1) – ((a – 1) × (r – 1)) = a×r×n – 1 – a + 1 – r + 1 – (a×r – r – a + 1) = a×r×n – a – r + 1 – a×r + r + a – 1 = a×r×n – a×r = a×r×(n – 1) или, что тоже самое kz = N – a × r = a×r×n – a × r = a×r×(n – 1) | kz = 6×3×(10 – 1) = | = 162 |
| OKC | kOKC = p – 1 | kOKC = 4 – 1 = | = 3 |
| CKC | kCKC = [p × (p – 3)]/2 | kCKC = [4×(4 – 3)]/2 = | = 2 |
| Исправленная | kе = kz × r × n | kе = 162 × 3 × 10 = | =4860 |
В таблице при определении числа степеней свободы остаточной (или средовой или случайной или экотипической) изменчивости исходим из представления о числе степеней свободы остаточной дисперсии как о разности между общим числом степеней свободы и степенями свободы всех организованных факторов (Гужов, Фукс, Валичек, 1991, стр. 334; Доспехов, 1973, стр. 167 – 168; Лакин, 1980, стр. 219, 221, 233).
Примечание
Предложенная схема расчетов имеет свои методические ограничения в части вычисления величины специфической комбинационной способности. В частности, число комбинаций скрещивания не может быть меньше 3. В противном случае число степеней свободы для СКС становится равным «0», что бессмысленно и делает деление на такую степень свободы невозможным, или будет отрицательным, что также бессмысленно.
a×b×(c – 1)×b×c = (a×b×c – a×b) × b×c =
(a – 1) × (r – 1) × n = (a×r – r – a +1) × n = a×r×n – r×n – a×n + n = a×r×n – (r×n + a×n) + n = a×r×n – n×(r + a) + n = a×r×n – n×(r + a) – 1)
Таблица ***
Дисперсионный анализ высоты 20-летних гибридов дуба
| Крите-рии | Варианты опыта - Гибридные комбинации (а) а=6 Фактор высшей иерархии | Сум-ма | |||||||||||||||||
| а1 (1х2) | а2 (1х3) | а3 (1х4) | а4 (2х3) | а5 (2х4) | а6 (3х4) | ||||||||||||||
| Повторности испытания потомства ( r=3) в каждой комбинации скрещивания Фактор низшей иерархии | |||||||||||||||||||
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | ||
| Hi | 5 ,5 | 5,9 | 6,4 | 6,5 | 6,0 | 6,3 | 3,0 | 3,5 | 4,0 | 3,1 | 4,1 | 3,9 | 2,5 | 4,1 | 4,0 | 3,5 | 4,1 | 2,8 |
|
| 5,4 | 6,1 | 6,0 | 6,5 | 5,9 | 6,1 | 3,4 | 3,4 | 4,1 | 3,0 | 3,0 | 3,9 | 4,1 | 2,6 | 4,1 | 3,5 | 4,0 | 2,9 | ||
| 6,0 | 6,1 | 6,2 | 6,1 | 5,8 | 5,4 | 2,8 | 3,4 | 3,2 | 2,8 | 3,6 | 3,6 | 4,1 | 4,1 | 4,1 | 3,8 | 4,0 | 4,9 | ||
| 6,2 | 6,3 | 5,8 | 5,5 | 6,3 | 5,0 | 3,2 | 3,2 | 3,1 | 2,6 | 3,4 | 3,5 | 3,9 | 3,9 | 4,0 | 3,5 | 4,1 | 4,1 | ||
| 6,1 | 5,8 | 5,9 | 5,4 | 6,5 | 6,5 | 3,0 | 2,8 | 2,5 | 3,4 | 2,8 | 3,5 | 3,5 | 3,6 | 4,9 | 2,8 | 4,0 | 4,0 | ||
| 6,4 | 5,7 | 5,7 | 4,9 | 5,2 | 6,3 | 3,0 | 2,8 | 2,5 | 3,0 | 2,8 | 2,5 | 3,5 | 3,8 | 3,9 | 4,1 | 3,9 | 3,8 | ||
| 6,1 | 5,1 | 5,0 | 6,1 | 6,3 | 6,0 | 2,9 | 2,0 | 3,8 | 2,5 | 2,9 | 3,4 | 3,9 | 3,8 | 3,9 | 4,1 | 3,9 | 3,8 | ||
| 6,0 | 6,4 | 6,0 | 6,3 | 6,2 | 5,9 | 2,8 | 4,1 | 2,1 | 2,1 | 3,1 | 3,8 | 4,0 | 4,1 | 3,8 | 4,0 | 3,2 | 3,8 | ||
| 5,9 | 6,0 | 6,2 | 6,4 | 6,1 | 5,8 | 3,6 | 4,1 | 3,0 | 2,9 | 3,2 | 4,0 | 4,9 | 3,6 | 3,5 | 2,9 | 3,1 | 3,4 | ||
| 6,0 | 6,1 | 6,3 | 6,3 | 6,1 | 5,6 | 3,4 | 2,1 | 3,1 | 3,1 | 3,4 | 4,0 | 2,6 | 3,8 | 3,5 | 3,9 | 2,9 | 3,0 | ||
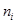
| 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | N=180 |
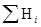
| 59,6 | 59,5 | 59,5 | 60 | 60,4 | 58,9 | 31,1 | 31,4 | 31,4 | 28,5 | 32,3 | 36,1 | 37 | 37,4 | 39,7 | 36,1 | 37,2 | 36,5 | ΣΣHi= 77 2 ,6 |
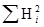
| 356,04 | 355,23 | 355,47 | 362,68 | 365,98 | 348,81 | 97,41 | 103,32 | 102,62 | 82,45 | 105,83 | 132,13 | 141,56 | 141,64 | 158,99 | 132,27 | 140,3 | 136,95 | ΣΣH2i=3615,81 |
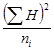
| 355,22 | 354,03 | 354,03 | 360,00 | 364,82 | 346,92 | 96,721 | 98,596 | 98,596 | 81,225 | 104,33 | 130,32 | 136,9 | 139,88 | 157,61 | 130,32 | 138,38 | 133,23 | (ΣHi)2 Σ-------- ni 3595,60 |
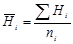
| 5,96 | 5,95 | 5,95 | 6 | 6,04 | 5,89 | 3,11 | 3,14 | 3,14 | 2,85 | 3,23 | 3,61 | 3,7 | 3,74 | 3,97 | 3,61 | 3,72 | 3,65 | ΣHi Σ-------- ni = 77,51 |
Решение задачи состоит из трех этапов.
1. доказательство существенности различий между гибридными комбинациями.
2. доказательство наличия эффектов комбинационной способности.
3. анализа комбинационной способности отдельных родителей и вариантов скрещивания.
1 этап.
Различия между гибридными комбинациями оцениваются по F критерию Фишера в двухфакторном дисперсионном комплексе (табл. ***).
1. Вычисляем общую сумму квадратов отклонений:
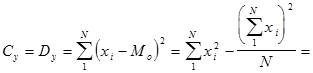
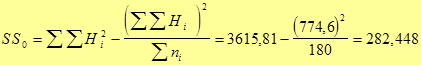 .
. 
2. На следующем этапе находим межгрупповой квадрат отклонений – общий факториальный квадрат отклонений:
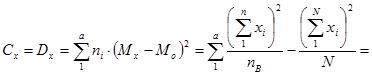
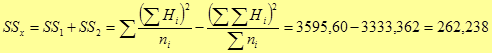
Здесь величина

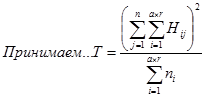
3. Далее находим вспомогательную промежуточную величину – сумму взвешенных квадратов сумм по фактору А (по отношению к числу вариант в пределах каждой соответствующей градации фактора А) для расчета суммы квадратов отклонений по фактору А:

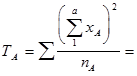
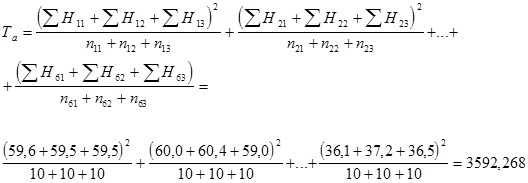
4. После этого определяем сумму квадратов отклонений по первому фактору – фактору высшего уровня иерархии (фактору А):
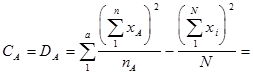
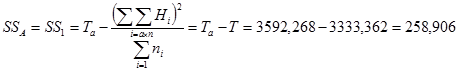
5. Рассчитываем остаточную сумму квадратов отклонений (по неорганизованным факторам), используя представление об остаточной дисперсии как о той доле её общей величины, которая представляет собой разность между общей дисперсией и дисперсией всех организованных факторов:
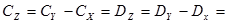
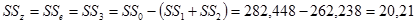
6. На следующем этапе вычисляем вариансы или средние квадраты отклонений: вариансу по первому фактору – различия между гибридными комбинациями (А) – ms1 и остаточную вариансу – по неорганизованным факторам (Z) – ms3 :
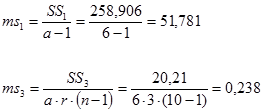
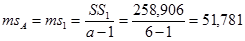
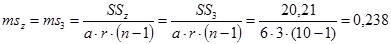
Примечание!
Источник ошибки в учебнике М.М. Котова (1997, стр. 136, 137 и далее) , согласно которой число степеней свободы остаточной дисперсии многофакторного комплекса равна ke = ( l –1)( n – 1), кроется в следующем выведении (В.П. Бессчетнов) указанного значения (из Доспехов, 1973, стр. 241) для однофакторного дисперсионного комплекса с повторностями:
N = n* l, тогда:
ke = (N-1) – (n-1) – (l-1) = (n*l – 1) – (n-1) – (l-1)= n*l – 1 – n +1 –l +1 = n*l – n –l +1 =
= n( l –1) –( l – 1) = ( l –1)( n – 1).
Б.А. Доспеховым (1973) справедливо предполагалось, что в однофакторном комплексе с повторностями не существует взаимодействия между собственно организованным фактором и его повторностями. Важно, что речь в этом случае идет именно об однофакторном комплексе.
Аналогичная неоднозначность (неточность, ошибка) опубликована в учебнике П.Ф. Рокицкого, 1978, стр. 266, 360 – 364 при интерпретации расчета величин ОКС и СКС(! У него же введен индекс m для обозначения числа степеней свободы остаточной (случайной) дисперсии без разъяснения как данный показатель формируется.
Г.Ф. Лакин (1980, стр. 233), рассматривая двухфакторные равномерные дисперсионные комплексы, предлагает следующую систему оценок степеней свободы:
N= a× b× n, где N – общая численность комплекса; a – число градаций фактора А; b – число градаций фактора В в пределах одного градации фактора А; n – численность одного варианта – одной градации фактора В.
ky = N – 1 = a×b×n – 1;
kx = a×b – 1;
kA = a – 1;
kB = b – 1;
kAB = (a – 1)×(b – 1);
kz = N – a×b = [a×b×n – 1] – [a – 1] – [b – 1] – [(a – 1)×(b – 1)] = a×b×n – 1 – a + 1 – b + 1 – [(a – 1)×(b – 1)] = a×b×n – a – b + 1 – [(a – 1)×(b – 1)] = a×b×n – a – (b – 1) – [(a – 1)×(b – 1)] = a×b×n – a – (b – 1) × [1 + (a – 1)] = a×b×n – a – (b – 1) × a = a×b×n – a – a×b + a = = a×b×n – a×b
7. В заключении находим критерий Фишера:
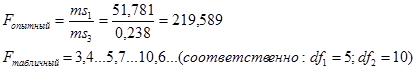
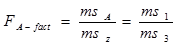
Сравнение фактического значения критерия Фишера с его табличным значением (на трех уровнях значимости) показывает наличие существенных различий между гибридными комбинациями.
2 этап.
1. Вычисляются средние высоты гибридов по вариантам скрещивания, включая все повторности. Результаты заносятся в диаллельную таблицу (табл. ****).
ВНИМАНИЕ!
В учебнике М.М. Котова (1997) не объясняется порядок заполнения таблицы!
При этом заполнение таблицы осуществляется так, что нижняя треугольная часть таблицы является соответствующим повторением её верхней треугольной части. В этом случае принимается во внимание тот факт, что обратных скрещиваний и самоопыления не проводилось. Тогда (!) в нижней треугольной части (!) будем иметь значения признака гибридного потомства, у которого номер материнского дерева является номером отцовского дерева, а номер отцовского – соответственно номером материнского.
Здесь уместнее было бы указать не номера отцовских и материнских деревьев, а «номера особей в прямых диаллельных скрещиваниях». Тогда становится понятным, что нижняя треугольная часть является соответствующим повторением (поскольку повторяются те же комбинации прямых скрещиваний) верхней треугольной части таблицы.
Таблица ****
| Номера отцовских деревьев | Номера материнских деревьев |
| |||
| 1 | 2 | 3 | 4 | ||
| 1 | - | 5,95 | 5,98 | 3,15 | 15,08 |
| 2 | 5,95 | - | 3,24 | 3,84 | 13,03 |
| 3 | 5,98 | 3,24 | - | 3,66 | 12,88 |
| 4 | 3,15 | 3,84 | 3,66 | - | 10,65 |
2. Находим общую полусумму средних значений высот деревьев – сумму одной из частей (верхней или нижней) полученной равномерной прямоугольной матрицы (только верхняя треугольная часть или только нижняя треугольная часть), т.е. суму значений признака (в нашем случае высоты деревьев) у особей, являющихся гибридным потомством при односторонних прямых диалльльных скрещиваниях.
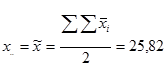
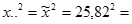
3. Подсчитываем суммы квадратов, обусловленные общей и специфической комбинационной способностью (SSg, SSs).
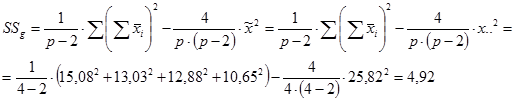
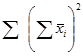
4. Подсчитываем суммы квадратов, обусловленные специфической комбинационной способностью (SSs):
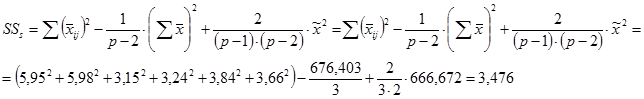
где:
р – число родительских пар.
5. Проводим дисперсионный анализ комбинационной способности (табл. ****):
Таблица ****
Дисперсионный анализ комбинационной способности
родительских деревьев дуба
| № | Источники варьирования | Сумма квадратов отклонений SS | Число степеней свободы df | Средний квадрат отклонений ms | Критерий Фишера опытный Fфактич. |
| 1. | Общая комбинационная способность | SSg=4,92 | df = p – 1 = 3 | 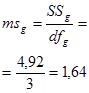
| 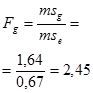
|
| 2. | Специфическая комбинационная способность | 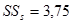
| 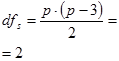
| 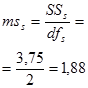
| 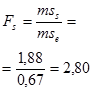
|
| 3. | Случайные отклонения | 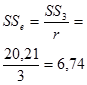
| 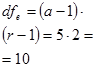 
| 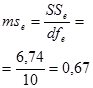
|  -
-
|
| Стандартные значения F | Fg = 3,8 – 7,0 – 13,1 Fs = 4,1 – 7,9 – 14,9 | ||||
Различия по общей и специфической комбинационной способности оказались недостоверными.
Если бы Fg был достоверен, можно было бы приступить к третьему этапу анализа.
3 этап.
Рассчитывается средний эффект (u) и эффекты общей комбинационной способности отдельных родителей (gi).
1. Рассчитываем средний эффект:
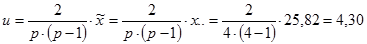
ВНИМАНИЕ!
Здесь уместнее объяснить, что средний эффект по сути является общим средним значением селектируемого (анализируемого) признака, отклонение от которого частного среднего значения признака гибридного потомства отдельного дерева во всех комбинациях его скрещивания со всеми остальными особями есть мера оценки ОКС.
Тогда предложенный алгоритм расчета общего среднего уместнее представить в более развернутой форме:
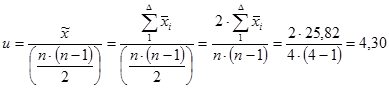 , где
, где
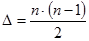 .
.
2. Рассчитываем эффекты общей комбинационной способности отдельных родителей:
ВНИМАНИЕ!
Возможно, приведен не точный алгоритм расчета.
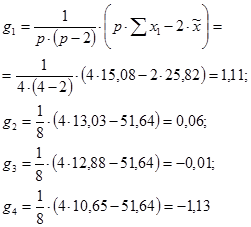
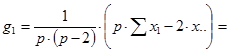
ВЫВОД.
Лучшей комбинационной способностью обладает первое дерево.
Сходный вывод напрашивается даже при общем знакомстве с исходными данными. В двух комбинациях из трех средняя высота гибридного потомства этого дерева почти в два раза превосходит высоту гибридных растений в других вариантах скрещивания.
ВНИМАНИЕ!
Скорее всего, более корректным будет алгоритм расчета, в котором при вычислении «средних» значений «контрольных» деревьев и полусибсового потомства, происходящего от одной особи и разных опылителей, в знаменателе первого сомножителя должна стоять разность между числом родительских пар и «единицей», а не «двойкой».
В этом случае ОКС каждого из родителей рассчитывается как разность между общим средним значение признака всех гибридов прямого диаллельного скрещивания во всех его комбинациях (когда растение выступает и как отцовское, и как материнское) и средним значение признака гибридного потомства одного из испытываемых родителей во всех комбинациях скрещивания, где одним (любым – материнским или отцовским) из родителей было испытываемое дерево.
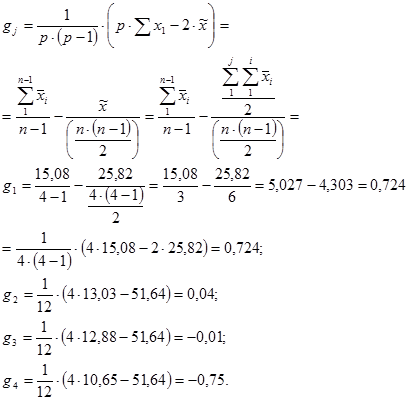
3. В случае достоверности mss далее вычисляются константы специфической комбинационной способности по формуле:
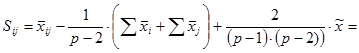
Для нашего примера получим:
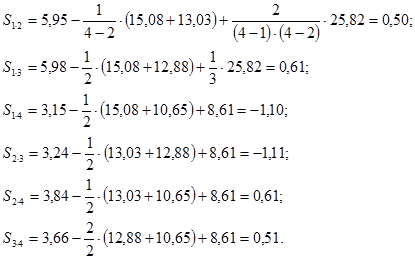
4. Полученные значения констант (Sij) заносим в следующую таблицу (табл.*****):
Таблица ****
Эффекты общей (gi), константы специфической (Sij) и
вариансы специфической комбинационной способности ( 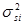 )
)
| Номера отцовских деревьев | Константы СКС по номерам материнских деревьев, Sij | Эффекты ОКС, gi
| Вариансы СКС,
| |||
| 1 | 2 | 3 | 4 | |||
| 1 | - | 0,50 | 0,61 | -1,10 | 1,11 | 0,56 |
| 2 | 0,50 | - | -1,11 | 0,61 | 0,06 | 0,60 |
| 3 | 0,61 | -1,11 | - | 0,51 | -0,01 | 0,60 |
| 4 | -1,11 | 0,61 | 0,51 | - | -1,13 | 0,59 |
5. Вычисляются вариансы специфической комбинационной способности по каждому дереву:
Скорректированный алгоритм:
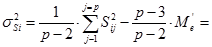
σ2Si =
По М.М. Котову (1997), запись несет в себе неточности, требующие коррекции, имеем:
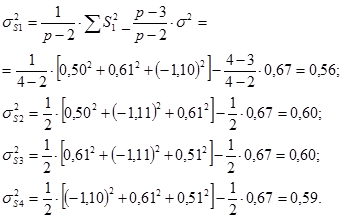
6. Значения варианс СКС по каждому дереву заносим в ту же таблицу (табл.***).
ВЫВОД.
По специфической комбинационной способности взятые для скрещивания деревья не отличаются друг от друга, на что и указывала раньше недостоверность mss.