Тема 2.2. Приложения производной
1.Правила дифференцирования.
2.Таблица производных: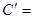 
…, 
…, 
…, 
…. 
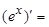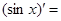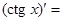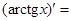
3.Таблица производных: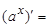 
…, 
…, 
…, 
….
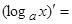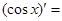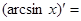4.Таблица производных: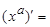 
…, 
…, 
…, 
….
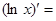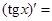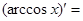5.Таблица производных: …, …, …,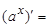 
….
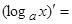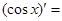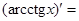6.Правило Лопиталя раскрытия неопределённостей.
7.Определение возрастающей функции.
8.Определение убывающей функции.
9.Теорема о необходимых условиях возрастания (убывания) функции.
10. Определение точки минимума функции.
11. Определение точки максимума функции.
12. Определение минимума и максимума функции. Определение экстремума функции.
13. Теорема: необходимые условия экстремума функции.
14. Определение критических точек первого рода.
15. Теорема: первое достаточное условие экстремума функции.
16. Теорема: второе достаточное условие экстремума функции.
17. Определение выпуклости графика функции.
18. Определение вогнутости графика функции.
19. Теорема об интервалах выпуклости и вогнутости графика функции.
20. Определение точки перегиба графика функции.
21. Теорема: достаточные условия существования точек перегиба (без доказательств)
Тема 3. Неопределенный интеграл
1.Определение первообразной.
2.Геометрическое представление неопределённого интеграла.
3.Свойства неопределённого интеграла: о постоянном множителе и сумме(разности) двух функций.
4.Свойства неопределённого интеграла: о производной и дифференциале от неопределённого интеграла.
5.Метод непосредственного интегрирования.
6.Метод внесения под знак дифференциала.
7.Метод замены переменной.
8.Метод интегрирования по частям: формула.
9.Метод интегрирования по частям: таблица замены.
10. Выделение полного квадрата (либо формула, либо показать на примере).
11. Разложение дроби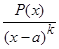 
на простейшие дроби.
12. Разложение дроби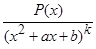 
на простейшие дроби.
13. Таблица интегралов: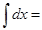 
……; 
….; 
…..; 
…….
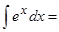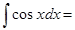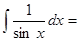14. Таблица интегралов: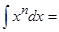 
…, 
…, 
…, 
….
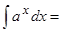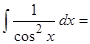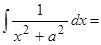15. Таблица интегралов: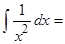 
…, 
…, 
…, 
….
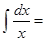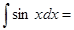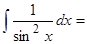Тема 4. Определенный интеграл
1.Таблица интегралов: ……; ….; …..; …….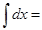
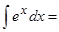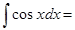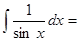2.Таблица интегралов: …, …, …, ….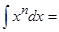
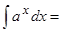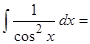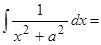3.Таблица интегралов: …, …, …, ….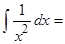
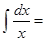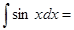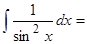4.Формула интегральной суммы с пояснениями.
5.Формула площади криволинейной трапеции с пояснениями.
6.Определение определённого интеграла.
7.Свойства определённого интеграла: интеграл с одинаковыми пределами интегрирования, перестановка пределов интегрирования.
8.Теорема о среднем для определённого интеграла (без доказательств).
9.Формула интеграла с переменным верхним пределом (с пояснением).
10. Формула Ньютона-Лейбница (с пояснением).
11. Замена переменной в определённом интеграле.
12. Формула интегрирования по частям в определённом интеграле.
13. Формула вычисления площади криволинейной трапеции, когда фигура ограничена двумя не пересекающимися кривыми.
14. Формула вычисления площади криволинейной трапеции, когда фигура ограничена двумя пересекающимися кривыми.
15. Определение несобственного интеграла.
16. Определение несобственного интеграла 1-го рода (одно из трёх).
17. Сходимость несобственного интеграла 1-го рода.
18. Определение несобственного интеграла 2-го рода (одно из трёх).
19. Сходимость несобственного интеграла 2-го рода.