При 180о, то есть когда векторы имеют противоположные направления, косинус равен минус единице, и соответственно результат будет отрицательным.
Группа: 23
Дата: 01.10.21 (2 пара)
Дисциплина: Математика
Тема урока: Скалярное произведение векторов.
Преподаватель: Старцева М.С.
Тип урока: Урок изучения нового материала.
Цель урока:
Цели
Образовательные:
- изучение скалярного произведения векторов в пространстве;
Развивающие:
- развитие пространственного воображения и логического мышления;
- развитие памяти, математической речи, наблюдательности, развитие графических навыков.
Воспитательные:
- воспитание интереса к предмету и потребности в приобретении знаний.
1. Организационный этап.
- Здравствуйте. Откройте тетради, запишите сегодняшнее число и тему урока «Угол между векторами. Скалярное произведение векторов».
Ход урока.
-Запишите определение:
Углом между ненулевыми векторами 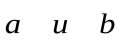 называется угол, образованный при откладывании этих векторов от одной точки.
называется угол, образованный при откладывании этих векторов от одной точки.
Обозначение: 

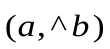
- Замечание:
Если векторы сонаправлены, то угол между ними равен 0 ° , а если векторы противоположно направлены, то угол между ними равен 180 ° .
- Введем определение скалярного произведения:
Определение:


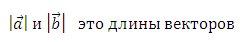
*Длина вектора (модуль) определяется следующим образом:
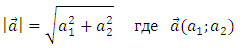
Данные формулы необходимо запомнить!!!
Покажем угол между векторами:
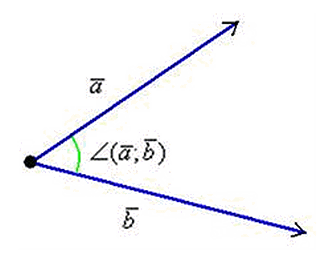
Понятно, что он может изменяться в пределах от 0 до 1800 (или в радианах от 0 до Пи).
Можем сделать некоторые выводы о знаке скалярного произведения. Длины векторов имеют положительное значение, это очевидно. Значит, знак скалярного произведения зависит от значения косинуса угла между векторами.
Возможны случаи:
1. Если угол между векторами острый (от 00 до 900), то косинус угла будет иметь положительное значение.
2. Если угол между векторами тупой (от 900 до 1800), то косинус угла будет иметь отрицательное значение.
*При нуле градусов, то есть когда векторы имеют одинаковое направление, косинус равен единице и соответственно результат будет положительным.
При 180о, то есть когда векторы имеют противоположные направления, косинус равен минус единице, и соответственно результат будет отрицательным.
При 90о, то есть когда векторы перпендикулярны друг другу, косинус равен нулю, а значит и СП равно нулю. Этот факт (следствие, вывод) используется при решение многих задач, где речь идёт о взаимном расположении векторов, в том числе и в задачах входящих в открытый банк заданий по математике.
Сформулируем утверждение: скалярное произведение равно нулю тогда и только тогда, когда данные векторы лежат на перпендикулярных прямых.
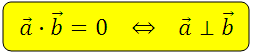
Итак, формулы СП векторов:
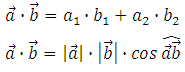
Если известны координаты векторов или координаты точек их начал и концов, то всегда сможем найти угол между векторами:
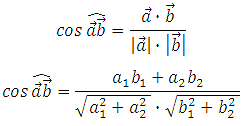
Свойства:
1. Для любых 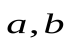 верно:
верно:

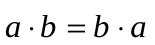
2. Для любых 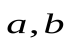 и любого действительного числа
и любого действительного числа 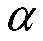 верно:
верно:
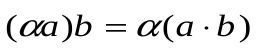
3. Для любых 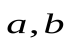 и
и 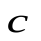 верно:
верно:
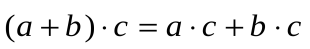
3. Закрепим новый материал:
Задача№1
Дано:
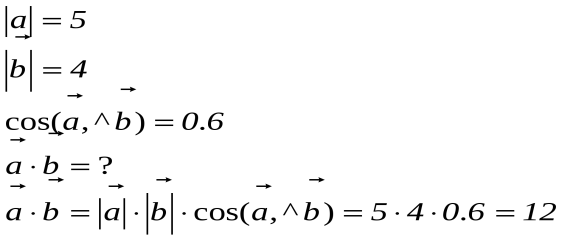
Задача№2
Дано:
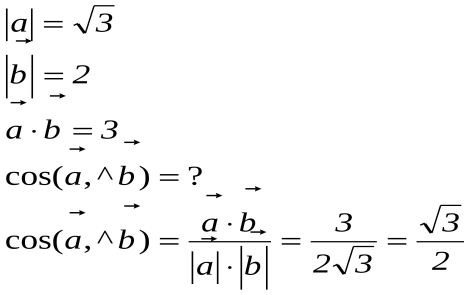
Задача№3
Дано:
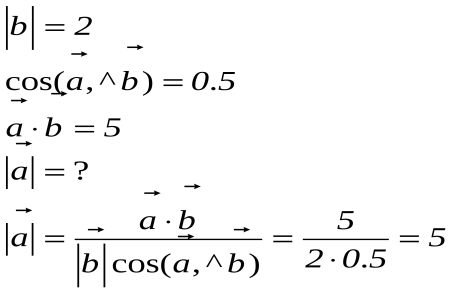
Задача№4
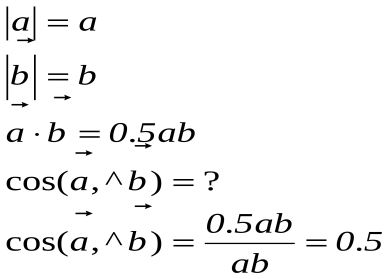
- Скалярное произведение определяется также через координаты. Запишите координатный вид скалярного произведения.
Пусть даны векторы:
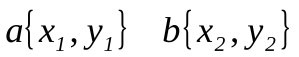
Тогда их скалярное произведение определяется формулой:
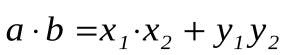 (сумма произведений абсцисс векторов и ординат векторов)
(сумма произведений абсцисс векторов и ординат векторов)
так как:
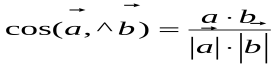 и
и 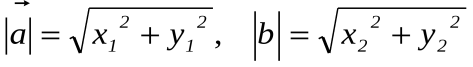
то через координаты формула нахождения косинуса угла между векторами выглядит следующим образом:
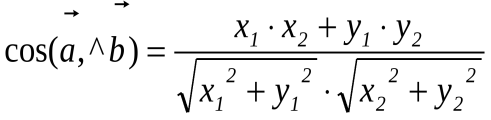
Если векторы взаимно перпендикулярны, то их скалярное произведение равно 0
Решим следующую задачу:
Найти скалярное произведение векторов:
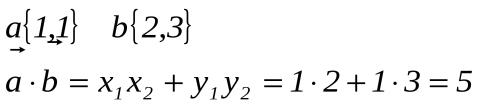
4. - Сегодня на уроке мы познакомились с понятием скалярного произведения векторов. Что является скалярным произведением векторов?
- По каким формулам можно найти косинус угла между векторами?
- Как находится абсолютная величина вектора?
5.Задания для закрепления :
Даны четыре точки A (0; 1; -1), B (1; -1; 2), C (3; 1; 0), D (2; -3; 1). Найдите косинус угла ф между векторами AB и CD.
Литература:
Погорелов А.В. Геометрия учеб. для 10-11кл.общеобразовательных учреждений А.В. Погорелов– М.: Просвещение, 2008.
https://vpr-rlass.com/uchebniki/matematika/10-11_klass_pogorelov_uchebnik_chitat_onlajn.html
Ответы предоставить в электронном формате с последующей отправкой на электронную почту: 37 ekaterina 37@ gmail . com








