Практическое занятие № 14. Графический метод расчёта параметров сетевого графика
При расчёте непосредственно на графике его вычерчивают с увеличенными размерами событий, каждое из которых делится на четыре сектора (рис. 14.1).
Расчёт ведётся в несколько этапов. Рассмотрим расчёт сети, приведённой на рис. 13.1.
Предварительно на модели (рис. 14.2) в верхнем секторе проставляют номера событий, а над стрелкой – продолжительности работ.
Затем определяют ранние начала работ. При определении ранних начал работ расчёт ведётся слева направо от исходного события к завершающему. За величину раннего начала принимается наибольшая продолжительность из всех путей, ведущих к данному событию.
| Номер события i |
| Раннее начало работы Б ТБРН |
| Позднее окончание работы А ТАПО |
| Номер начального события предшествующей работы, по которой проходит путь максимальной продолжительности |
| Работа А |
| Работа Б |
Рис. 14.1. Содержание секторов событий при расчёте на графике
Раннее начало работ, выходящих из события «1», равно нулю; затем определяем ранний срок начала работ 2-3 и 2-4. 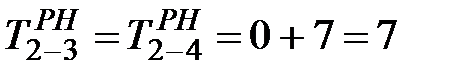 дн. Раннее начало записывается в левый сектор события «2». Одновременно в нижний сектор записывают номер начального события предшествующей работы, по которой проходит путь максимальной продолжительности от первого события модели до рассматриваемого. В данном случае это событие «1».
дн. Раннее начало записывается в левый сектор события «2». Одновременно в нижний сектор записывают номер начального события предшествующей работы, по которой проходит путь максимальной продолжительности от первого события модели до рассматриваемого. В данном случае это событие «1».
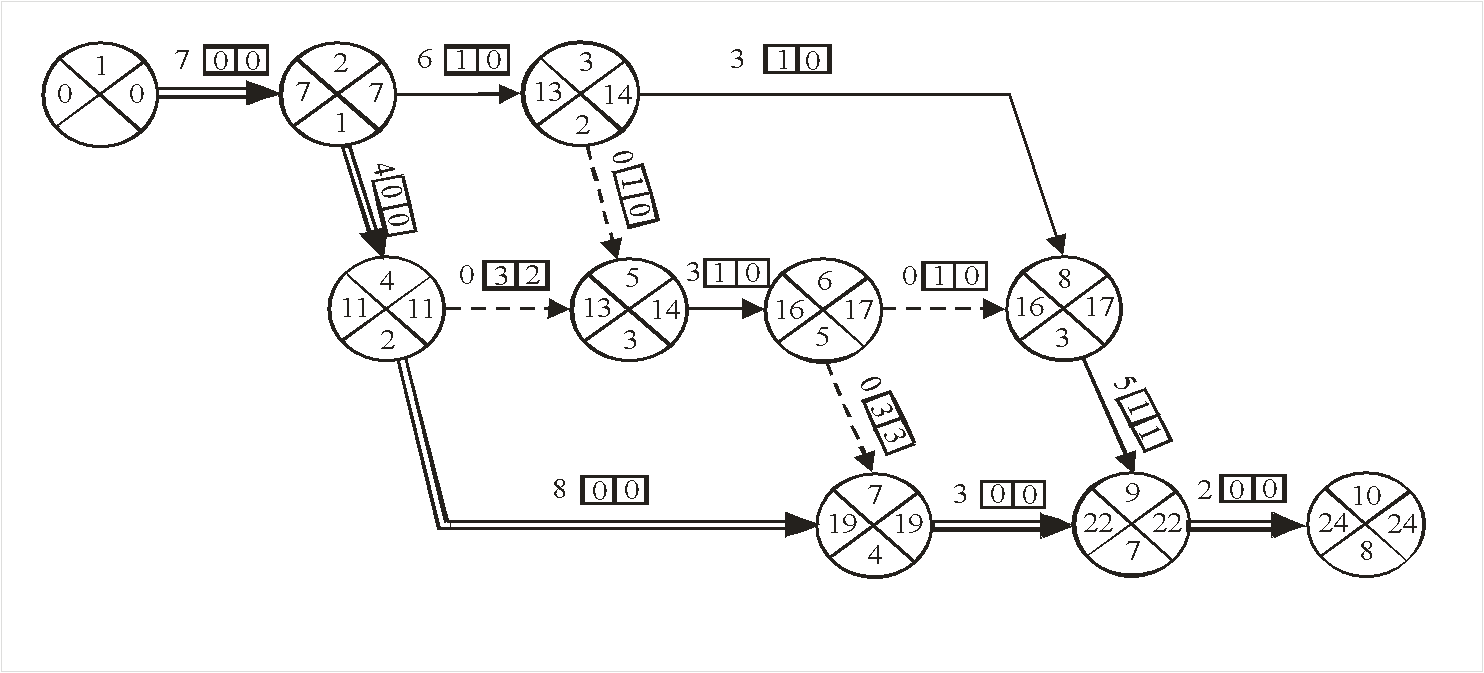
Рис. 14.2. Расчёт на графике
Аналогичным образом заполняются левый и нижний сектора всех событий, включая завершающее (событие «10»), левый сектор которого определит продолжительность критического пути: tкр = 24 дня.
Второй этап – определение позднего окончания работ. Расчёт ведётся справа налево от завершающего к начальному событию графика; при этом заполняются правые сектора.
Для завершающего события «10» значение левого сектора переносят в правый, так как в последнее событие входит критическая работа, а это значит, что позднее начало равно раннему окончанию, а последнее равно раннему началу последующей работы, значение которого записано в левом секторе.
Позднее окончание любой работы сетевого графика равно наименьшей разности поздних окончаний последующих работ и их продолжительности. Так, поздний срок окончания работы 7-9 равен 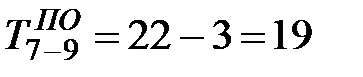 дн. Для работы 5-6 позднее окончание равно наименьшей разности из двух возможных:
дн. Для работы 5-6 позднее окончание равно наименьшей разности из двух возможных: 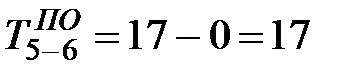 дн.,
дн., 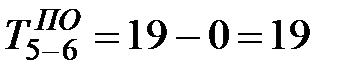 дн. В правый сектор записываем «17». Аналогичным образом определяются поздние окончания остальных работ сетевого графика. Если вычисления выполнены правильно, то в правом секторе исходного события получится ноль.
дн. В правый сектор записываем «17». Аналогичным образом определяются поздние окончания остальных работ сетевого графика. Если вычисления выполнены правильно, то в правом секторе исходного события получится ноль.
На третьем этапе определяем резервы времени по ранее приведённым формулам (13.5) и (13.6). Так, для работы 9-10 резервы времени будут следующие: R9-10 = 24 – (22 + 2) = 0; r9-10 = 24 – (22 + 2) = 0.
На четвёртом этапе определяется критический путь, проходящий через события, у которых правые и левые сектора равны между собой, а резервы времени равны нулю.








