Векторная форма записи системы.
Пусть 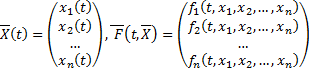 . Тогда система (2.14.1) можно записать в виде
. Тогда система (2.14.1) можно записать в виде

 Опр. Вектор-функция
Опр. Вектор-функция 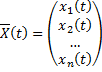 называется частным решением системы (2.14.1) на
называется частным решением системы (2.14.1) на 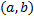 , если при ее подстановке в (2.14.1) все уравнения системы (2.14.1) обращаются в тождества на
, если при ее подстановке в (2.14.1) все уравнения системы (2.14.1) обращаются в тождества на 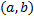 .
.
Задача Коши для системы (1).
Найти частное решение 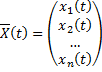 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям

где точка 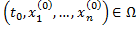 .
.
В векторной форме начальные условия имеют вид

где 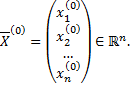
Опр. Семейство вектор-функций 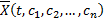 , зависящих от
, зависящих от 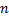 произвольных постоянных, называется общим решением системы (2.14.1), если
произвольных постоянных, называется общим решением системы (2.14.1), если
1. 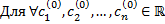 вектор-функция
вектор-функция 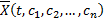 является частным решением.
является частным решением.
2. Для 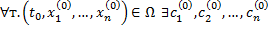 такие, что
такие, что 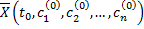 удовлетворяет начальному условию (2.14.2).
удовлетворяет начальному условию (2.14.2).
Векторная форма общего решения -
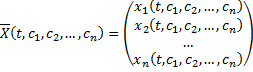 .
.
Теорема существования и единственности решения задачи Коши для нормальных систем.
Пусть функции  и их частные производные
и их частные производные 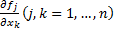 непрерывны в области
непрерывны в области 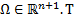 огда
огда 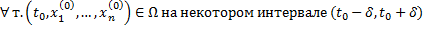
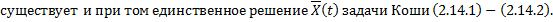
Сведение ДУ n-го порядка к нормальной системе. Рассмотрим ДУ -го порядка

Введем обозначения:
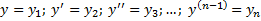 .
.
Тогда уравнение (2.14.3) равносильно системе
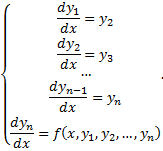
Пример.
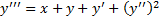 .
.
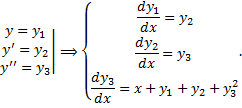
Сведение нормальной системы к одному уравнению n-го порядка.
Рассмотрим случай 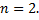
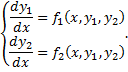
Сведем к ДУ 2-го порядка. Из 1-го уравнения
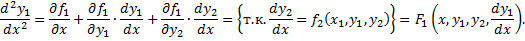
Если из 1-го уравнения системы можно выразить 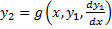 , то для
, то для 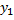 получим уравнение 2-го порядка:
получим уравнение 2-го порядка:
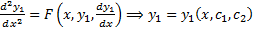 (общее решение ДУ 2-го порядка).
(общее решение ДУ 2-го порядка).
Тогда 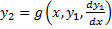 .
.
Пример.
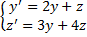 .
.
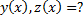
Продифференцируем 1-е уравнение:
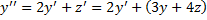 .
.
Из 1-го уравнения:
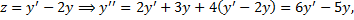
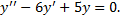
Характеристическое уравнение полученного ЛОДУ с постоянными коэффициентами:
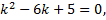
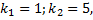
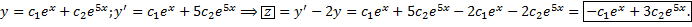
2.15.Автономные системы ДУ. Фазовое пространство и фазовые траектории. Первые интегралы систем ДУ. Симметричная форма записи систем ДУ и ее применение к нахождению первых интегралов.
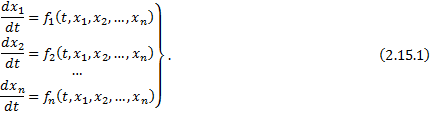
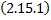 – нормальная система ОДУ.
– нормальная система ОДУ.
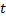 – независимая переменная,
– независимая переменная,
 – независимые функции,
– независимые функции,
 – определены в области
– определены в области 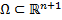 .
.
Если  не зависят явно от
не зависят явно от 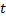 , то система (2.15.1) является автономной.
, то система (2.15.1) является автономной.
Фазовая плоскость.
Рассмотрим 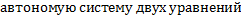

Пусть вектор-функция 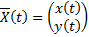 – частное решение автономной системы
– частное решение автономной системы 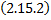 . Рассмотрим на плоскости
. Рассмотрим на плоскости 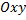 кривую
кривую 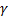 , заданную параметрическими уравнениями
, заданную параметрическими уравнениями

Кривая 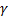 – фазовая кривая системы
– фазовая кривая системы 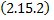 на фазовой плоскости
на фазовой плоскости 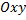 . Если система
. Если система 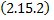 удовлетворяет условию теоремы существования и единственности, т.е.
удовлетворяет условию теоремы существования и единственности, т.е. 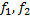 имеют непрерывные частные производные первого порядка в области
имеют непрерывные частные производные первого порядка в области 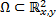 , то через каждую точку области
, то через каждую точку области 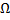 проходит ровно одна фазовая кривая.
проходит ровно одна фазовая кривая.
Касательный вектор к фазовой кривой в произвольной точке (см. рис. 41):
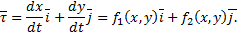
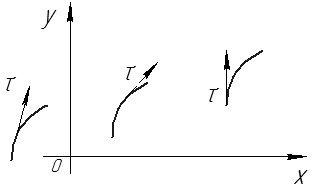
Рис. 41
Рассмотрим 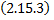 как функцию
как функцию 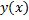 , заданную параметрически, тогда
, заданную параметрически, тогда
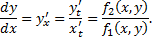
Таким образом фазовые кривые системы 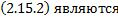 интегральными кривыми ДУ 1-го порядка
интегральными кривыми ДУ 1-го порядка
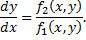
Пример.
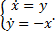
ДУ фазовых кривых:
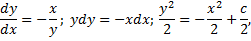
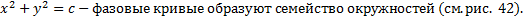
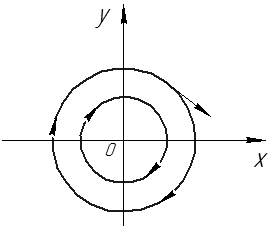
Рис. 42
Первые интегралы нормальных систем ДУ.
Опр. Равенство
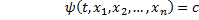

называется первым интегралом системы 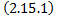 в области
в области 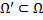 , если выполняется 2 условия:
, если выполняется 2 условия:
1. Функция 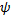 имеет непрерывные частные производные 1-го порядка в области
имеет непрерывные частные производные 1-го порядка в области 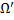 и для
и для 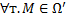
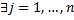 , что
, что 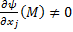 .
.
2. Для 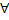 решения системы
решения системы 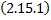
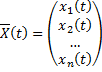
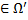
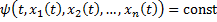 .
.
Первый интеграл позволяет понизить число уравнений в системе. Пусть в т. 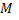
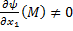 . Тогда по теореме о неявной функции из
. Тогда по теореме о неявной функции из 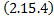 можно в некоторой окрестности т.
можно в некоторой окрестности т. 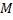 выразить
выразить 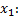
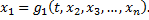
Подставив 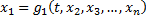 в уравнения системы
в уравнения системы 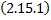 , начиная со второго, получим систему из (n-1) уравнения:
, начиная со второго, получим систему из (n-1) уравнения:
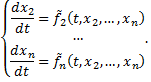
Чтобы полностью решить систему 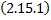 , нужно знать
, нужно знать 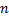 независимых первых интегралов:
независимых первых интегралов:

Независимость первых интегралов означает, что ни один из них не может быть выражен через остальные. Система 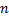 независимых первых интегралов
независимых первых интегралов 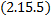 неявно задает решение системы.
неявно задает решение системы.
Симметричная форма записи нормальных систем ДУ:

Получив из симметричной формы системы интегрируемые комбинации (полные дифференциалы), можно найти 1-е интегралы. При нахождении интегрируемых комбинаций удобно использовать следующее свойство пропорций:
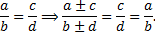
Пример 1.
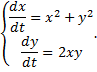
Симмметричная форма системы:
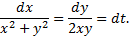
По свойству пропорций получаем
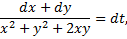
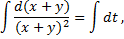
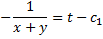
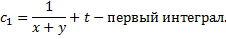
Аналогично
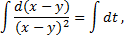
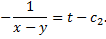
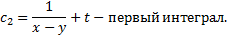
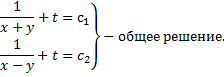
Пример 2.
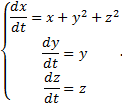
Для автономной системы найдем два независимых 1-х интеграла, не содержащих 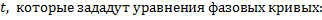
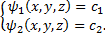
Симметричная форма системы:
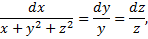
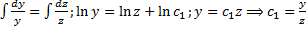 - (1-й интеграл).
- (1-й интеграл).
Чтобы найти второй 1-й интеграл запишем симметричную форму системы в виде
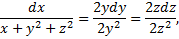
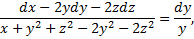
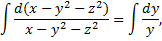
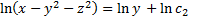 ,
,
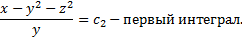
Таким образом, найденные первые интегралы задают фазовые кривые системы:
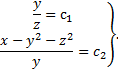
Пример 3.
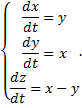
Симметричная форма:
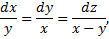
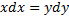 ,
,
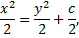
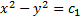 - 1-й интеграл.
- 1-й интеграл.
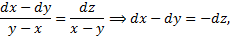
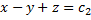 - 1-й интеграл.
- 1-й интеграл.
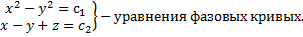
2.16.Нормальные системы ЛДУ, однородные и неоднородные. Матричная запись системы. Линейность пространства решений системы ЛОДУ. Вронскиан системы вектор-функций и его свойства. Теорема о размерности пространства решений системы ЛОДУ. Структура общего решения. Фундаментальная система решений.
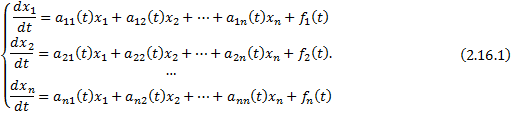
– нормальная система ЛНДУ, здесь 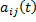 ,
, 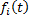 – функции, непрерывные на некотором интервале
– функции, непрерывные на некотором интервале 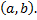
Если 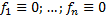 , то
, то 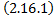 – система ЛОДУ.
– система ЛОДУ.
Матричная форма системы ЛДУ 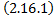 :
:

где
матрица 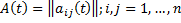
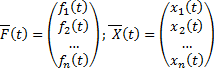 .
.
Соответствующая 

Теорема. Множество всех частных решений системы ЛОДУ 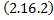 является линейным пространством относительно операций сложения вектор-функций и их умножения на число.
является линейным пространством относительно операций сложения вектор-функций и их умножения на число.
Док-во: пусть 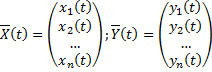 – решения системы
– решения системы 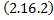 . Рассмотрим вектор-функцию
. Рассмотрим вектор-функцию 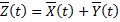 . Имеем
. Имеем
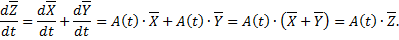
т.е. 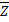 – решение
– решение 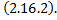
Аналогично при 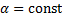 и вектор-функции
и вектор-функции 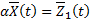 получаем
получаем
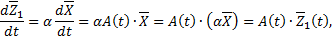
т.е. 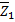 удовлетворяет системе
удовлетворяет системе 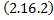
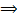 решения
решения 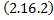 образуют линейное пространство.
образуют линейное пространство. 








