Построение ФСР ЛОДУ с постоянными коэффициентами по корням характеристического уравнения.
1. Случай различных действительных корней.
Пусть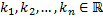 
- различные корни характеристического уравнения. Тогда функции
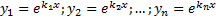
образуют ФСР ЛОДУ.
Док-во:
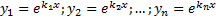– частные решения, т.к. 
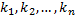- корни характеристического уравнения. Покажем, что 
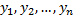– линейно независимы.
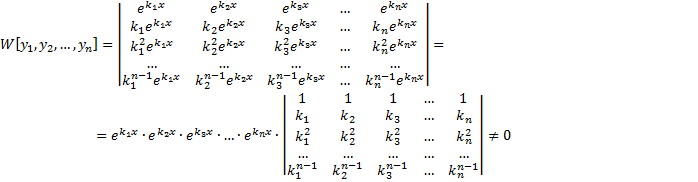
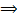
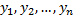– линейно независимы.
( 
При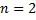 
: 
).
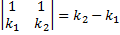Тогда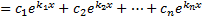 
.
Пример.
.
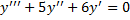Характеристическое уравнение:
,
,
,
,
.
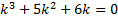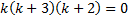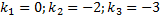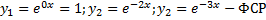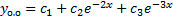2. Случай кратных действительных корней.
Пусть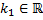 
- корень кратности 
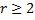, т.е.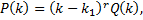 
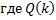– многочлен, причем 
.
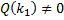Корню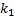 
кратности 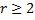соответствует 
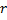линейно независимых решений:
.
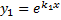
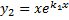
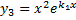
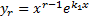Док-во: (для n=2)
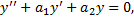
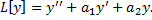
Пусть 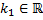- корень кратности 
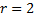характеристического уравнения
.
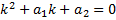Тогда по теореме Виета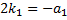 
.
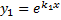– решение, т.к. 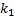– корень.
Покажем, что 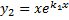– также решение:
.
( 
).
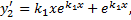
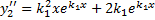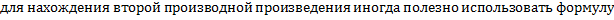
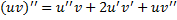Тогда
.
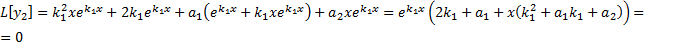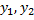– решения, линейно независимые, т.к.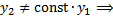 
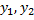– ФСР ЛОДУ с постоянными коэффициентами 2-го порядка и кратным корнем .
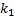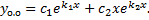
Пример.
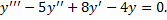
Характеристическое уравнение:
,
,
.
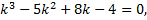
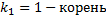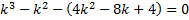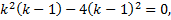
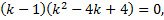
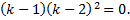
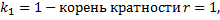
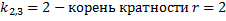ФСР: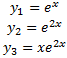 
.
3. Случай комплексных корней кратности 1.
Пусть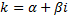 
– корень характеристического уравнения кратности 1 
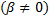. Тогда 
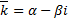– также корень кратности 1. Паре корней 
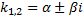соответствуют 2 линейно независимых решения:
.
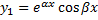
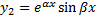Док-во:
Рассмотрим комплексную показательную функцию, которую введем по формуле Эйлера
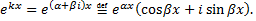
Покажем, что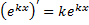 
при :
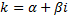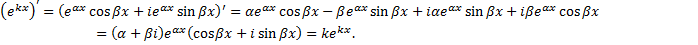
Тогда для функции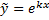 
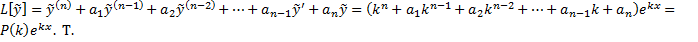е. 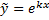– комплексное решение ЛОДУ с постоянными коэффициентами.
Т.к.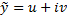 
– решение, то 
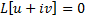, т.е. 
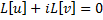, т.е. функции
,
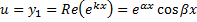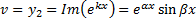
– решения ЛОДУ, они линейно независимы, т.к.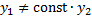 
.
Примеры.
1. 
.
,
,
,
.
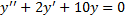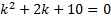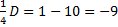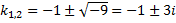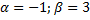ФСР: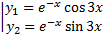 
,
.
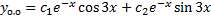2. 
.
,
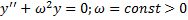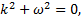
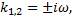
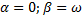ФСР: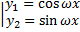 
.
.
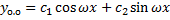4. случай кратных комплексных корней (возможен только при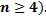 
Пусть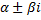 
– корни кратности , 
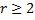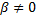. Им соответствуют 
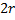линейно независимых решений:
.
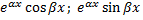
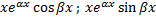
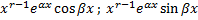2.12. Нахождение частных решений неоднородного ЛДУ с постоянными коэффициентами и правой частью специального вида.
Пусть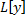 
– линейный дифференциальный оператор с постоянными коэффициентами. Рассмотрим ЛНДУ:
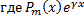– квазимногочлен;
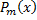– многочлен степени 
;
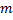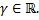
Тогда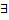 
частное решение ЛНДУ (2.12.1) вида
,
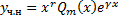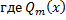– многочлен степени ; 
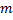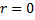, если 
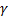не является корнем характеристического уравнения соответствующего ЛОДУ; если 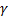– корень, то 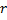равен кратности корня .
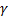Замечание. Коэффициентыв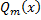 
- неопределенные (заранее не неизвестные), находятся методом неопределенных коэффициентов.
Пример 1.
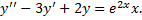
Соответствующее ЛОДУ: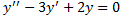 
,
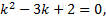
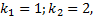
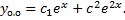
Найдем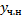 
.
;
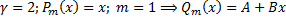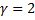– корень характеристического уравнения ЛОДУ кратности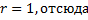 
,
,
,
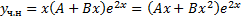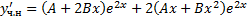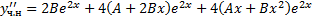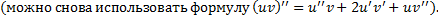
Чтобы найт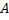и 
и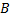 
, подствим функцию в ЛНДУ:
,
,
,
.
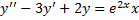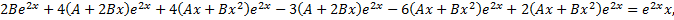
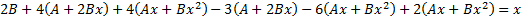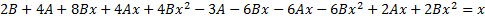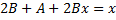Коэффициент при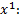 
2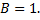 
Коэффициент при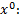 
.
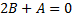Получаем СЛАУ относительно 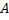и 
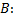
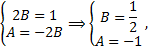
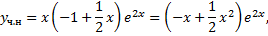
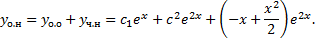
Рассмотрим ЛНДУ с постоянными коэффициентами
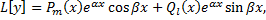
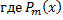– многочлен степени ;
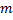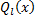– многочлен степени 
;
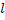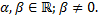
Тогда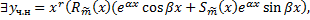 
; 
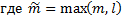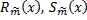– многочлены степени 
;
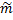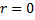, если 
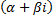не является корнем характеристического уравнения соответствующего ЛОДУ; 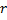равен кратности корня, если 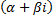является корнем.
Пример 1.
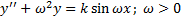
(уравнение колебаний при наличии внешней периодической силы частоты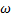 
).
.
,
,
,
.
.
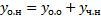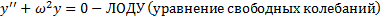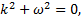
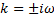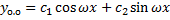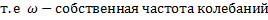Найдем .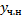
,
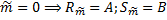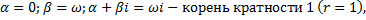
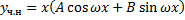
(частота внешней силы равна собственной частоте 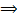резонанс, амплитуда колебаний неограниченно возрастает).
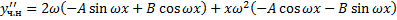
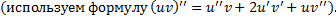
Чтобы найт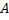и и 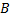, подставим 
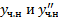в ЛНДУ:
.
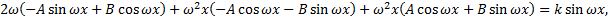
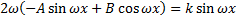Коэффициент при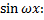 
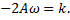
Коэффициент при 
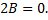
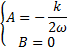
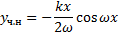
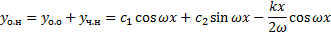
Пример 2.
,
,
,
,
,
,
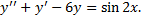
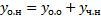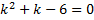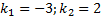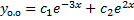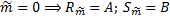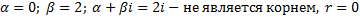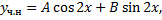
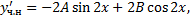
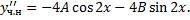
Чтобы найт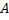и и 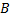, подствим в ЛНДУ:
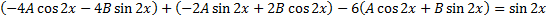
Коэффициент при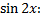 
.
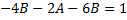Коэффициент при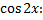 
.
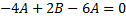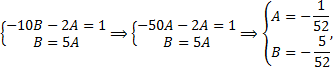
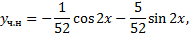
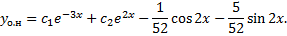
2.13. Метод вариации постоянных решения неоднородных ЛДУ n-го порядка (вывод для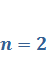 
).
Пусть 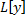– линейный дифференциальный оператор с переменными коэффициентами. Рассмотрим ЛНДУ:
Соответствующее ЛОДУ:
Общее решение ЛОДУ:
.
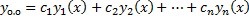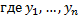– ФСР ЛОДУ,
– произвольные постоянные.
Теорема. Общее решение ЛНДУ (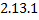 
) имеет вид
,
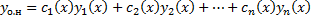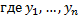– ФСР соответствующего ЛОДУ,
производные функций 
определяются из СЛАУ
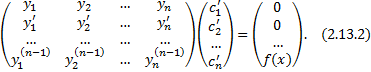
Замечание 1. СЛАУ (2.13.2) имеет единственное решение для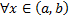 
, т.к. ее определитель 
( ).
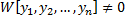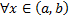Замечание 2. Функций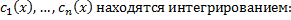 
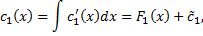
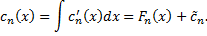
Тогда
,
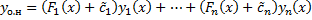– произвольные постоянные.
Док-во (случай 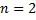). Рассмотрим ЛНДУ
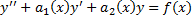
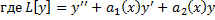– линейный дифференциальный оператор 2-го порядка.
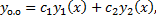
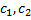– произвольные постоянные
СЛАУ (2.13.2) имеет вид
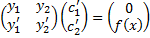, или
.
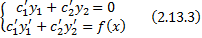1. Покажем, что если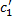 
и 
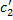удовлетворяют (2.13.3), то функция 
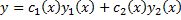– решение ЛНДУ (2.13.1).
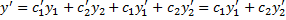
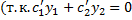в силу (2.13.3)).
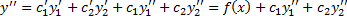
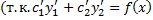в силу (2.13.3)).
Тогда
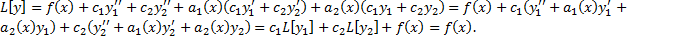
Таким образом 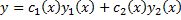– решение ЛНДУ (2.13.1).
2. Решив СЛАУ (2.13.3), получим решение вида
.
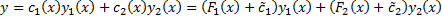Покажем, что для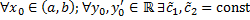 
, такие, что решение 
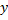, соответствующее 
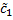и 
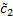, удовлетворяет начальным условиям
.
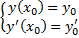Для 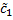и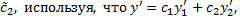 
получим систему
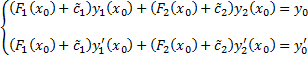
- СЛАУ с определителем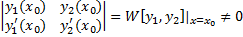 
, т.к. 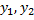– ФСР ЛОДУ,
т.е.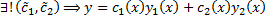 
– общее решение.
Пример.
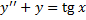
(метод неопределенных коэффициентов неприменим!).
Соответствующее ЛОДУ:
,
,
,
,
,
,
,
,
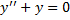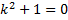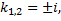
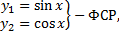
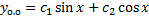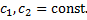
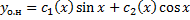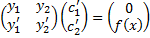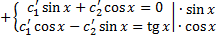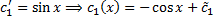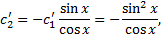
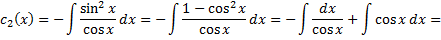
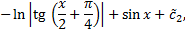
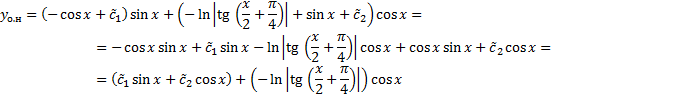
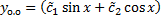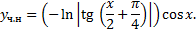
2.14. Нормальные системы ДУ. Задача Коши и теорема существования и единственности ее решения. Сведение ДУ n-го порядка к нормальной системе. Сведение нормальной системы к одному уравнению n-го порядка.
(2.14.1) – нормальная система ОДУ.
– независимая переменная,
– неизвестные (искомые) функции,
– определены в области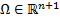 
.
Если не зависят явно от 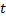, то система (2.14.1) называется автономной.