Практическое занятие № 8. Оптимизация неритмичных потоков с целью сокращения сроков строительства
При организации неритмичных потоков, когда в роли захваток выступают здания (объекты), важно установить оптимальную очерёдность их возведения, обеспечивающую кратчайший срок строительства.
Количество возможных вариантов, устанавливающих очерёдность возведения объектов, среди которых находится оптимальный, зависит от числа объектов и определяется числом перестановок (К!). Если в нашем примере 4 объекта и нужно решить при какой очередности (при прочих равных условиях) будет обеспечен кратчайший срок их возведения, то возможно рассмотрение 4! перестановок, т.е. 4 x 3 x 2 x 1 = 24 вариантов. Из этого следует, что путь полного перебора является громоздким и трудоёмким.
В рассматриваемой методике описываются более простые способы, основанные на использовании матричного алгоритма. На рис. 8.1 повторен выполненный выше расчёт неритмичного потока с введением двух дополнительных граф.
На основании суммарной продолжительности каждого процесса на всех объектах находим поток наибольшей длительности и выделяем его двойной линией (второй процесс). Этот процесс принимается за ведущий, в известной мере определяющий срок строительства. Затем по каждой строке матрицы подсчитывается время, предшествующее ведущему процессу ( 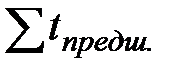 ) и следующее после него (
) и следующее после него ( 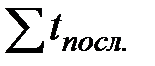 ). Результаты заносятся в первую дополнительную графу. Если ведущим потоком является первый или последний, то
). Результаты заносятся в первую дополнительную графу. Если ведущим потоком является первый или последний, то 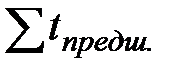 или
или 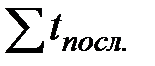 соответственно обращаются в нуль.
соответственно обращаются в нуль.
Помимо 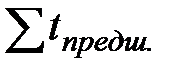 и
и 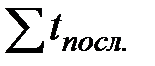 рекомендуется также определять разность между продолжительностями последнего и первого процессов с записью результатов во вторую дополнительную графу матрицы с соответствующим знаком (рис. 8.1).
рекомендуется также определять разность между продолжительностями последнего и первого процессов с записью результатов во вторую дополнительную графу матрицы с соответствующим знаком (рис. 8.1).
|
| Процессы | | tn – t1 | |||||||||||||
| 1 | 2 | 3 | 4 | |||||||||||||
| Объекты | I | 0 | 4 | 14 | 20 | 4 | – 2 | |||||||||
|
| 4 |
|
| 6 |
| 4 | 6 |
|
| 2 |
| |||||
| 8 | ||||||||||||||||
| 4 | 10 | 20 | 22 | |||||||||||||
| II | 4 | 10 | 20 | 22 | 5 | – 4 | ||||||||||
|
| 5 |
| 1 | 5 |
|
| 1 |
|
| 1 |
| |||||
| 2 | ||||||||||||||||
| 9 | 15 | 21 | 23 | |||||||||||||
| III | 9 | 15 | 21 | 23 | 4 | + 2 | ||||||||||
|
| 4 |
| 2 | 2 |
| 4 | 1 |
|
| 6 |
| |||||
| 7 | ||||||||||||||||
| 13 | 17 | 22 | 29 | |||||||||||||
| IV | 13 | 17 | 22 | 29 | 1 | + 3 | ||||||||||
|
| 1 |
| 3 | 5 |
|
| 1 |
| 6 | 4 |
| |||||
| 5 | ||||||||||||||||
| 14 | 22 | 23 | 33 | |||||||||||||
4+5+4+1=14 < 6+5+2+5=18 < 6+1+1+1=9 > 2+1+6+4=13
Рис. 8.1. Исходная матрица для оптимизации неритмичного потока
На основании двух дополнительных граф необходимо составить матрицу с новой очередностью возведения объектов согласно следующим правилам.
В первую строку матрицы записывается объект с наименьшим значением 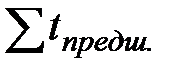 (числитель) и наибольшим значением разности, а в последнюю – объект с наименьшим значением
(числитель) и наибольшим значением разности, а в последнюю – объект с наименьшим значением 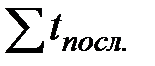 (знаменатель) и наименьшим значением разности tn - t 1 .
(знаменатель) и наименьшим значением разности tn - t 1 .
Затем заполняются вторая и предпоследняя строки матрицы с условием, чтобы 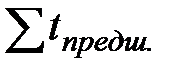 и
и 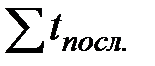 постепенно увеличивались при перемещении внутрь матрицы, а значение разности изменялось бы от максимума в первой строке до минимума в последней (рис. 8.2).
постепенно увеличивались при перемещении внутрь матрицы, а значение разности изменялось бы от максимума в первой строке до минимума в последней (рис. 8.2).
В случае, если изложенные выше правила распределения объектов по строкам матрицы противоречат друг другу, то рекомендуется применять их порознь, т.е. сначала построить одну матрицу, руководствуясь значениями 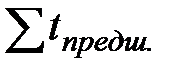 и
и 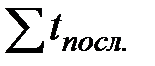 , а затем другую – по разностям продолжительностей
, а затем другую – по разностям продолжительностей
| min à max |
последнего и первого процессов (tn – t1).
|
| Процессы | | tn – t1 | |||||||||||||
| 1 | 2 | 3 | 4 | |||||||||||||
| Объекты | IV | 0 | 2 | 13 | 14 | 1 | + 3 | |||||||||
|
| 1 |
| 1 | 5 |
| 6 | 1 |
|
| 4 |
| |||||
| 5 | ||||||||||||||||
| 1 | 7 | 14 | 18 | |||||||||||||
| III | 1 | 7 | 14 | 18 |
| + 2 | ||||||||||
|
| 4 |
| 2 | 2 |
|
| 1 |
|
| 6 |
| |||||
| 7 | ||||||||||||||||
| 5 | 9 | 15 | 24 | |||||||||||||
| I | 5 | 9 | 15 | 24 | 4 | – 2 | ||||||||||
|
| 4 |
|
| 6 |
|
| 6 |
|
| 2 |
| |||||
| 8 | ||||||||||||||||
| 9 | 15 | 21 | 26 | |||||||||||||
| II | 9 | 15 | 21 | 26 | 5 | – 4 | ||||||||||
|
| 5 |
| 2 | 5 |
| 1 | 1 |
| 4 | 1 |
| |||||
|
| ||||||||||||||||
| 14 | 20 | 22 | 27 | |||||||||||||
Рис. 8.2. Рациональная очередность возведения объектов
Произведенный расчёт показал, что при новой очередности возведения объектов срок строительства сократится на 6 принятых единиц времени по сравнению с первоначальным вариантом, что составляет 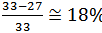 .
.
Указанный метод определения очередности строительства объектов в 80% случаев даёт сокращение сроков строительства.
Матрице с рис. 8.2 будет соответствовать представленная ниже циклограмма неритмичного потока и график потребности рабочих (рис. 8.3).
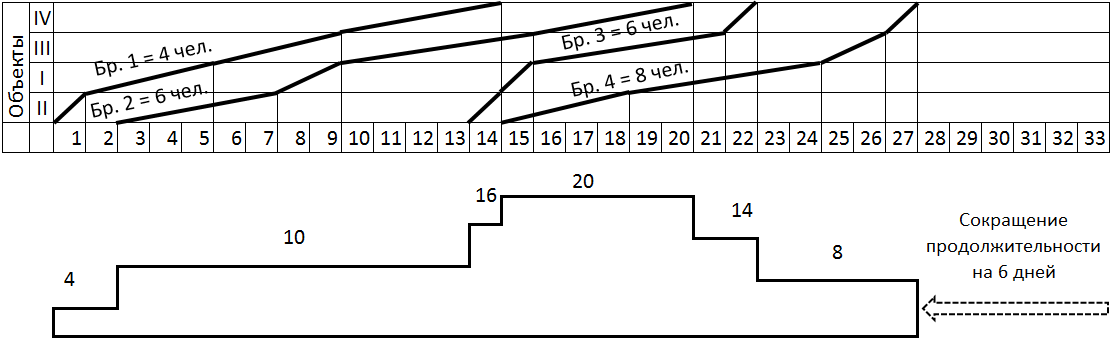
Рис. 8.3. Циклограмма неритмичного потока и график потребности рабочих
Сокращение сроков строительства может быть достигнуто также за счёт совмещения процессов, когда последующий процесс начинают, не дожидаясь полного окончания предыдущего.
На рис. 8.4 показан рассмотренный выше неритмичный поток, выполняемый совмещено благодаря разбивке каждого объекта на две захватки. Произведённый расчёт показывает, что общий срок строительства уменьшился до 23,5 принятых единиц времени, что составляет 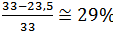 по сравнению с первоначальным вариантом.
по сравнению с первоначальным вариантом.
| Процессы | ||||||||||||||
| Объекты и захватки |
| 1 | 2 | 3 | 4 | |||||||||
| IV | а | 0 | 0,5 | 10 | 10,5 | |||||||||
| 0,5 | 2,5 |
| 0,5 | 2 | ||||||||||
| 0,5 | 3 | 10,5 | 12,5 | |||||||||||
| б | 0,5 | 3 | 10,5 | 12,5 | ||||||||||
| 0,5 |
| 2,5 |
| 5 | 0,5 |
| 1,5 | 2 | ||||||
| 1 | 5,5 | 11 | 14,5 | |||||||||||
| III | а | 1 | 5,5 | 11 | 14,5 | |||||||||
| 2 |
| 2,5 | 1 |
| 4,5 | 0,5 |
| 3 | 3 | |||||
| 3 | 6,5 | 11,5 | 17,5 | |||||||||||
| б | 3 | 6,5 | 11,5 | 17,5 | ||||||||||
| 2 |
| 1,5 | 1 |
| 4 | 0,5 |
| 5,5 | 3 | |||||
| 5 | 7,5 | 12 | 20,5 | |||||||||||
| I | а | 5 | 7,5 | 12 | 20,5 | |||||||||
| 2 |
| 0,5 | 3 |
| 1,5 | 3 |
| 5,5 | 1 | |||||
| 7 | 10,5 | 15 | 21,5 | |||||||||||
| б | 7 | 10,5 | 15 | 21,5 | ||||||||||
| 2 |
| 1,5 | 3 |
| 3 |
| 3,5 | 1 | ||||||
| 9 | 13,5 | 18 | 22,5 | |||||||||||
| II | а | 9 | 13,5 | 18 | 22,5 | |||||||||
| 2,5 |
| 2 | 2,5 |
| 0,5 |
| 4 | 0,5 | ||||||
| 11,5 | 16 | 18,5 | 23 | |||||||||||
| б | 11,5 | 16 | 18,5 | 23 | ||||||||||
| 2,5 |
| 2 | 2,5 | 0,5 |
| 4 | 0,5 | |||||||
| 14 | 18,5 | 19 | 23,5 | |||||||||||
Рис. 8.4. Сокращение срока строительства путём деления объектов на захватки
Матрице с рис. 8.4 будет соответствовать представленная ниже циклограмма неритмичного потока и график потребности рабочих (рис. 8.5).
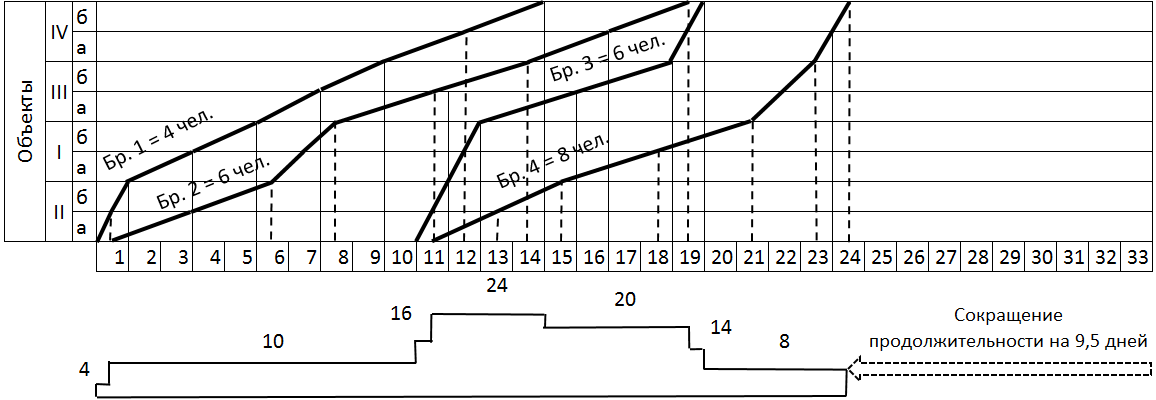
Рис. 8.5. Циклограмма неритмичного потока и график потребности рабочих